基于LC振荡电路的情境化仿真教学
作者: 赵勇 宋敏中图分类号:G633.7 文献标识码:A文章编号:1003-6148(2025)4-0083-5
1引言
L C 振荡电路,也称为谐振电路,是由一个电感 ( L ) 和一个电容 ( C ) 连接在一起的电路。它是许多电子设备中的关键部件[1。同时, L C 振荡电路也是高中物理电磁学的重要内容[2-3]。学生要理解该电路的工作原理,就需要掌握电容和电感的概念及其工作原理。为了帮助学生深入理解L C 振荡电路,可以通过虚拟仿真技术来模拟该电路,实现该电路的情境化教学。
目前,模拟 LC 振荡电路的方法有两种。一种是“半过程”情境仿真,即先把求解出来的电流、电量等参数方程录人到Geogebra等数学仿真软件中进行动态描绘。另一种是全过程情境模拟,即直接把电路图输入到MatlabSimulink等电路仿真软件中[4-6],然后由软件根据内置方程求解器计算电流、电压、电量等参数,并绘制这些参数的动态变化。全过程情境仿真更接近实物实验,仿真结果更容易受电路中各元件参数的影响。
COMSOLMultiphysics(简称COMSOL)是基于有限元分析的工程仿真软件[7-9],其根植于数学物理理论,从底层的理论出发,可以轻松实现各种物理现象的情境化仿真。因此,本文以 L C 振荡电路为例,尝试使用COMSOL全过程仿真,探究电容、电感及电阻对 L C 振荡电路性能的影响。为学生提供实践经验,拓展学生对电路认识的深度和广度,提升学生的科学思维素养。
2 LC振荡电路模型
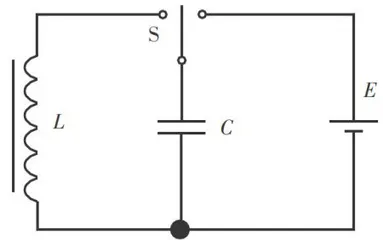
根据电感和电容的连接方式, L C 振荡电路可分为 L C 并联振荡电路和 L C 串联振荡电路[10]。在人教版普通高中教科书《物理选择性必修第二册》中,将线圈、电容器、电源和单刀双掷开关按图1所示组成一个 L C 串联振荡电路。先让开关与电源连接给电容器充电,然后开关向线圈一侧电路闭合。此时, L C 串联振荡电路中的电流和电压等信号会发生周期性变化。
3 COMSOL仿真过程
3.1 模型定义
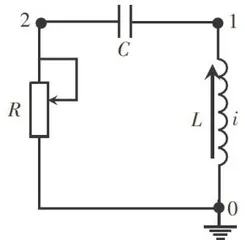
利用COMSOL物理场仿真软件中的电路功能,建构电路模型。在利用COMSOL建模前,需对图1中的电路进行简单变换。因为软件仿真时可以直接定义初始条件,不需要单刀双掷开关。另外,COMSOL电路搭建需要节点设置和接地条件。节点0、1、2用于组装电路时定义元器件的接电端口,其中节点0接地。为模拟情境化仿真电路中内阻(损耗电阻)对振荡信号的影响,还需在电路中添加一个滑动变阻器,如图2所示。
3.2 模型建构与计算
首先,在新建窗口中,单击“模型向导一零维”。在物理场中,选择“AC/DC—电路”。研究类型选择“一般研究—瞬态”。在“组件1—电路”中,添加接地点,选择节点名称为0。接着添加电感器, 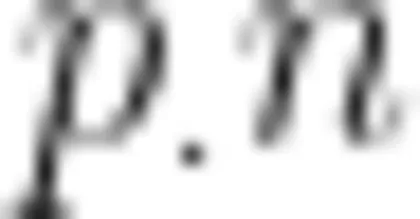 点分别选择节点0和1,如图3(a)所示。然后添加电容器和电阻,电容器和电阻的 p )n 节点分别是1、2和2、0。将电容器的初始电压设定为1V,这与教材中电容充电的初始条件相对应。之后,在参数1中定义电阻 R 电感 L 、电容 C 、电流Current和周期 T 的值,如图3(b)所示。再在“研究1—瞬态—设置"中,把“输出时步"设定为
点分别选择节点0和1,如图3(a)所示。然后添加电容器和电阻,电容器和电阻的 p )n 节点分别是1、2和2、0。将电容器的初始电压设定为1V,这与教材中电容充电的初始条件相对应。之后,在参数1中定义电阻 R 电感 L 、电容 C 、电流Current和周期 T 的值,如图3(b)所示。再在“研究1—瞬态—设置"中,把“输出时步"设定为 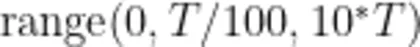 ,时间单位为s。“输出时步"指计算的时间从0开始,到10个振荡周期 ( T ) 结束,计算时间间隔为
,时间单位为s。“输出时步"指计算的时间从0开始,到10个振荡周期 ( T ) 结束,计算时间间隔为 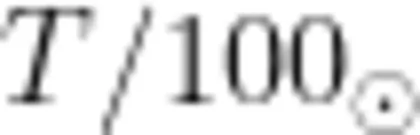 至此,整个模型建构完成。
至此,整个模型建构完成。
3.3 模型计算
点击“计算”,可得到计算结果。在“组件1一定义"中添加探针,便可从计算结果中调取电流、电压、节点电压等数据。为方便研究,可以把探针分为几个节点组。一组用来测元器件中的电流,一组测元器件终端电压,还有一组测各节点电压。当损耗电阻不为零时,还可以探测电阻的功耗或者热消耗。选取探针绘图组中的探针表图,就能情境化仿真振荡电路中的周期性变化的物理量。
4情境化仿真教学设计
4.1 L C 振荡电路情境化仿真设计
为了系统地研究 LC 振荡电路中电感、电容及损耗电阻等参数对电流和电压曲线的影响,制订了图4所示的情境化仿真设计方案。首先,设定损耗电阻 ( R=0 ) ,分别固定电容 c 和电感 L ,研究调控 L 和 C 时的电流、电压等参数的变化曲线。然后,假定存在损耗电阻 ( R>0 ) ,分别研究损耗电阻 R 变化而 L 和 C 不变以及损耗电阻 R 不变而 L 和 c 变化时的电流、电压曲线。
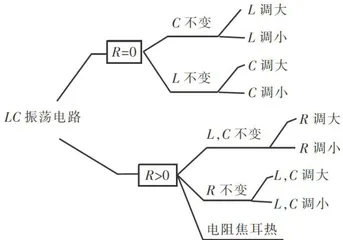
图4振荡电路情境化仿真设计
本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:wlst20250420.pd原版全文
4.2 理想 L C 振荡电路的情境化仿真
仿真前,教师要引导学生:当 L C 振荡电路中的消耗内阻 R=0 时,不会产生热消耗。此时,L C 振荡电路处于理想状态,没有能量损耗。电容的电流和电压(或极板带电量)都应该做谐振运动。因此,可通过情境化仿真实验,检验电流和电压曲线是否处于谐振状态。
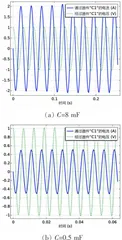
首先,将图3(b)中的 R 值改为0,其他参数( L=2m H, C=2m F) 保持不变,可得电流和电压的变化曲线,如图5(a)所示。需要指出的是,电容和电感的电流、电压曲线相似,图中仅展示电容器元件的电流和电压曲线。另外,由于电流和电压值的单位不同,所以纵坐标没有标明物理量单位,两条曲线对应的纵坐标值分别以A和V为单位。可以看出,电流和电压确实处于谐振状态,随时间呈现周期性振荡。 t = 0 时,电压最大、电流为零,这表明电压超前电流,即先有电容电压(初始值为1V,电容放电后在电路中形成电流。根据 L C 振荡电路的周期公式 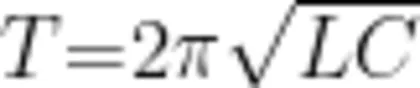 ,可得振荡周期 T≈0 . 0 1 2 6s ,这与图中的变化周期一致。当把 L 调至原来的4倍( 8 m H 时,电流的振幅变为原来的 1 / 2 ,周期变为原来的2倍
,可得振荡周期 T≈0 . 0 1 2 6s ,这与图中的变化周期一致。当把 L 调至原来的4倍( 8 m H 时,电流的振幅变为原来的 1 / 2 ,周期变为原来的2倍 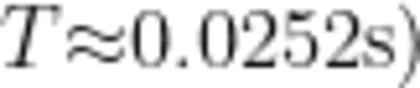 ,如图5(b)所示。这说明,电感增大后,电流减小,周期增大,但电容器电压的振幅不变。相反,把L调至原来的 1 / 4 ( 0 . 5 m H) 时,电流的振幅变为原来的2倍,周期变为原来的1/2( T≈0 . 0 0 6 3s) ,如图5(c)所示。
,如图5(b)所示。这说明,电感增大后,电流减小,周期增大,但电容器电压的振幅不变。相反,把L调至原来的 1 / 4 ( 0 . 5 m H) 时,电流的振幅变为原来的2倍,周期变为原来的1/2( T≈0 . 0 0 6 3s) ,如图5(c)所示。
教师根据以上结果设置问题:为什么电感增大后,电流减小?学生根据教师的问题进行分组讨论。教师对各组的讨论表现进行评价后,对该现象的原因进行总结:根据电磁感应定律,线圈经过变化的电流可以产生磁场,变化的磁场会感应出电动势,进而产生感应电流。再由楞次定律,感应电流所产生的磁场总是阻碍原来的磁场。因此,当电感经过交流电时,感应电流会阻碍变化的电流(交流电),导致电流的振幅变小。
然后,教师引导学生:通过 L C 振荡电路的情境化仿真实验,我们发现了电感器有抑制变化的交流电的作用。那么,电容器在电路中又起什么作用呢?我们可以尝试增大电容,并观察电路信号的变化情况来探究这个问题。
实验设计: L 不变,分别将 c 调为原来的4倍和1/4,且初始电流为0A、初始电压为1V时,仿真结果分别如图6(a)(b)所示。可以看出,当 c 为原来的4倍时,电流的振幅和周期都为原来的2倍,但电压的振幅不变;当 C 为原来的1/4时,电流的振幅和周期都为原来的1/2,电压的振幅也不变。这些结果表明,增加电容的容量会增大电流的幅值,但不会改变电压的幅值。

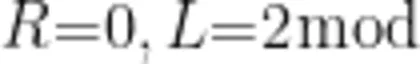
平均电流,即 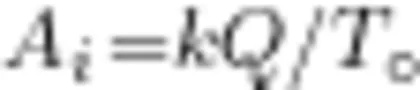 其中, k 为无量纲的比例系数, Q 为电容带电量, T 为振荡周期。又由于Q = C U ,
其中, k 为无量纲的比例系数, Q 为电容带电量, T 为振荡周期。又由于Q = C U , 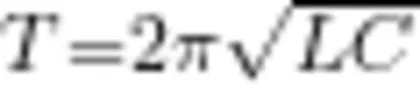 ,可得
,可得
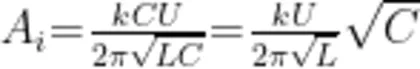
由于 k , U 和 L 都不变,所以电流幅值 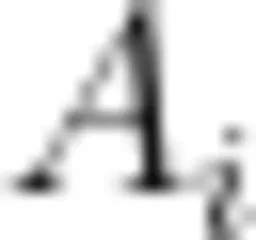 正比于
正比于 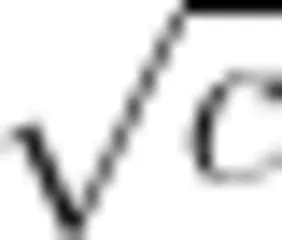 。
。
教师提问:增加电容的容量,电压的振幅一定不变吗?
教师引导学生讨论上述问题并评价后,给出答案:在情境化仿真的参数设置中,电感器的初始电流为0A,电容器的初始电压设置为1V(电压的振幅固定)。所以,增大电容无法改变最大电压值。如果电容器初始电压为0V(电压振幅可调),电感器的初始电流设置为1A(电流振幅固定)。由于电容器的最大电量 Q = I T , I 为一个振荡周期内的平均电流,它与电流振幅 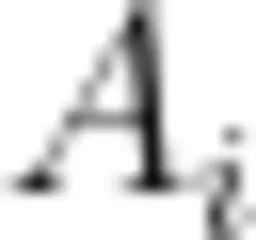 成正比,即
成正比,即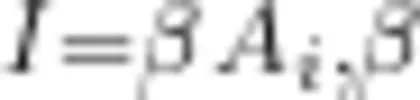 为比例系数。所以,
为比例系数。所以, 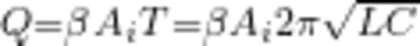 。那么,电压为
。那么,电压为
本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:wlst20250420.pd原版全文