科研学术反哺教学在网络空间安全学科中的教学探索与实践
作者: 王怀习 束妮娜 王晨 常超 马春来 张海燕中图分类号:G642 文献标志码:A 文章编号:2096-000X(2025)13-0022-0
Abstract:Scientificresearchandacademic fedback teachingisanimportantteaching methodproposedinmoder higher education,whichishelpfultopromotetheteachingcontentstokeeppacewiththetimes,cultivatestudents’innovativeand experimentalability,andachievethecoordinateddevelopmentbetween teachingandscientificresearchwork.Asanemerging discipline,cyberspacesecurityisupdatedrapidlyintermsofknowledgeandtechnologyandscientificresearchandacademic fedbackandteachinghasbecomeaninevitablerequirementforthedevelopmentofthisdiscipline,anditisalsotheneedto cultivatehigh-qualtycyberspacesecuritytalents.Thispapertakesthespecificteachingcasestodemonstratetheteaching practiceofscientificresearchacademicfeedbackteachingmethodinthecultivationofcyberspacesecuritydisciplinetalents,and summarizestheteachingmethodofscientificresearchacademicfedback teachingonthebasisof teachingpractice,inorderto providereferenceforsiilarmajorsindomesticuniversities tocarryoutscientificresearchandacademicfedbackteachingwork.
Keywords:scientificresearch andacademic fedback teaching;cyberspace security;network science;betweennesscentrality; cryptography; secret sharing
人才培养与科学研究是现代大学的基本职能,两者相互影响、相互矛盾,是相互促进、相互依赖的统一体。如何处理好教学与科研的关系是高等院校需要长期探索与实践的现实问题,也是高校教师亟须解决的重要问题[-2。近年来,国家出台一系列措施重点纠治高校中存在的“重科研、轻教学"的倾向性问题,牢固树立教学在高校工作中的中心地位。科研学术反哺教学是教育主管部门着力推行的教学方法,这是一种有效促进教学与科研协调发展的路径,助力于提升教学质量,为高素质的人才培养提供基础和保障。
信息时代条件下,知识更新与技术迭代加速推进,而传统教材更新迭代速度慢、周期较长,以教材为本的知识传授式的教学方式无法使学生获取最新的专业知识与工程技术,也就无法快速地适应未来工作岗位的需求。科研学术反哺教学通过将最新的科研学术成果引入课堂教学,实现教学内容的与时俱进、教学课堂与未来应用的有机衔接,有助于提升学生学习的积极性与目标性,更好地培养学生的创新意识和科学精神,培养学生的科研学术能力,能够有效提升学生的眼界与能力。
一科研学术反哺教学实践
此处笔者给出在网络空间安全学科研究生数学基础课程教学中采用的科研学术反哺教学案例,阐述科研学术成果如何反哺课堂教学,分别选取了介数恒等式以及拉丁方与秘密分享方案。这些教学案例选自组合数学-4与具体数学课程中的教学实例,科研学术成果选自于网络科学理论与密码学等网络空间安全学科专业主干课程的近期学术成果,包含了教学团队的学术思考,希望在数学基础课堂教学中拓展学员的专业视野,引导学生在课程学习中开展深度思考,学以致用。期望两个教学案例的阐述能够起到抛砖引玉、交流促进之功效。
(一)介数恒等式——具体数学与网络科学
1问题引入
复杂系统中元素之间相互作用,动态演化,不同元素的功能千差万别,影响迴异。为了形象地刻画元素间的相互影响,常常采用复杂网络结构来展示复杂系统的内部关系。因此,将复杂系统内的元素抽象为网络顶点,元素间的关系抽象为网络的边,边既可以是有向的,也可以是无向的,依赖于复杂系统运行机理-7。给定网络表示形式,网络科学研究人员定义了度量顶点和边的重要性的各种参数,如度数中心性、介数中心性、特征向量中心性等,其中顶点介数和边介数在关键顶点和关键链路识别时,具有广泛的应用场景。
2介数中心性概念
在授课时,引导学生学习网络科学中顶点介数与边介数的概念。以社会网络为例,一个人在网络中的介数中心性取决于该个体在多大程度上参与了网络中最优信息传递路径;以计算机网络为例,一个路由器的介数中心性取决于该路由器在路由网络信息传递中的重要性。介数概念假定系统运行遵循最简原则,网络中信息传播和社会交往遵循最短路径原则。
顶点介数定义:网络 G = ( V , E ) 中顶点 ν 的介数为
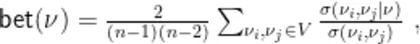
本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:gjxk20251306.pd原版全文
式中: V 为网络 G 的顶点集, 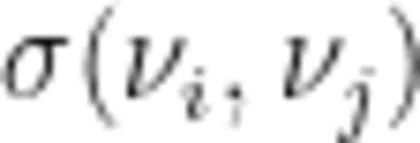 为顶点
为顶点 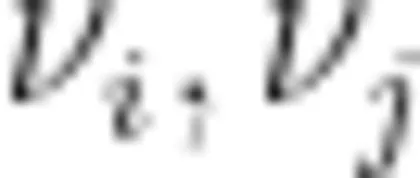 间最短路径的数目,
间最短路径的数目, 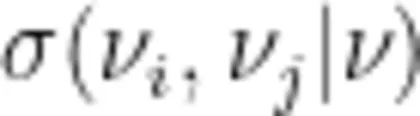 从
从 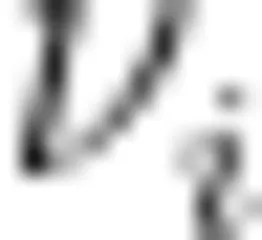 到
到 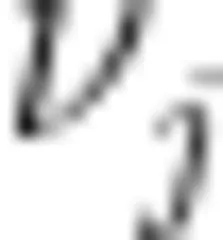 经过顶点 ν 的最短路径的数目。
经过顶点 ν 的最短路径的数目。
顶点介数标记了网络中经过顶点 ν 的所有最短路径的占比,相应地,边介数标记了网络中经过边 e 的所有最短路径的占比,由此自然引出边介数的定义。
边介数定义:网络 G = ( V , E ) 中边 e 的介数为
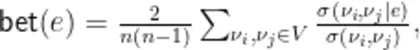
式中: 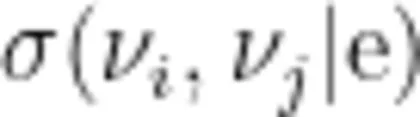 从
从 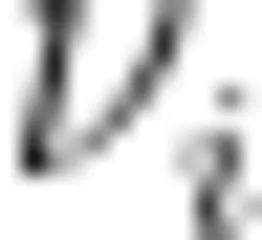 到
到 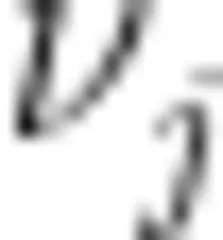 经过边
经过边 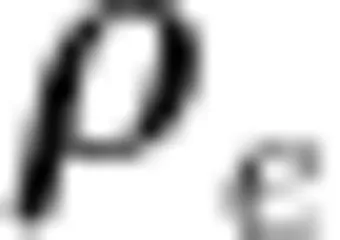 的最短路径的数目。
的最短路径的数目。
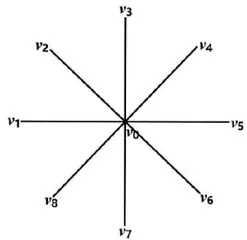
为了强化学生对介数的认知,选取“来"字型星型网络,其中心顶点为 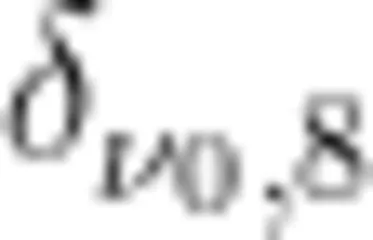 个边缘顶点分别为
个边缘顶点分别为 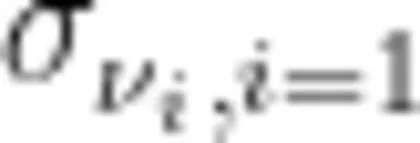 2 , ⋅ s , 8 ,中心顶点
2 , ⋅ s , 8 ,中心顶点 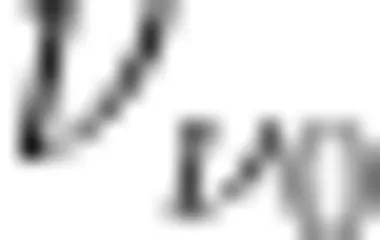 和每个边缘顶点
和每个边缘顶点 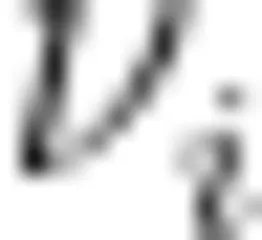 相连,边缘顶点之间无边相连,如图1所示。
相连,边缘顶点之间无边相连,如图1所示。
根据顶点介数的定义,引导学生计算“米"字型网络中顶点的介数。由于星型网络的对称性与顶点间最短路径的唯一性,遍历星型网络中最短路径得到中心顶点 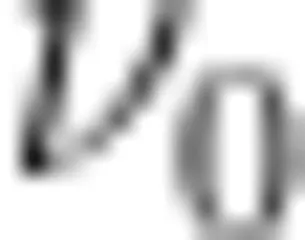 的介数为
的介数为 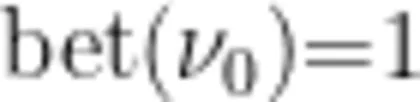 ,边缘顶点
,边缘顶点 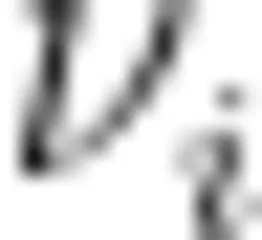 的介数为bet
的介数为bet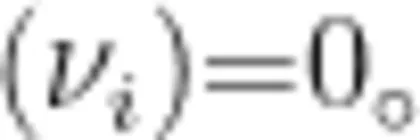 因此,中心顶点承载了网络中不同顶点间信息交互的全部中转工作,在网络信息传输中起着核心作用。若网络中心顶点出现故障,网络顶点均成为孤立顶点,整个网络连接彻底瘫痪,从中可以看出星型网络结构的脆弱性。
因此,中心顶点承载了网络中不同顶点间信息交互的全部中转工作,在网络信息传输中起着核心作用。若网络中心顶点出现故障,网络顶点均成为孤立顶点,整个网络连接彻底瘫痪,从中可以看出星型网络结构的脆弱性。
3介数恒等式与和式计算
介数有哪些重要性质?选择若干具体网络实例,计算其中顶点介数与边介数,引导学生观察介数分布特点,容易发现存在一个有趣的现象:随着连通无向简单网络规模的增长,顶点介数值快速减少,大量顶点介数值趋近于零。这一现象背后的原因是什么呢?经过深入研究,我们发现在无向连通网络中顶点介数与边介数蕴含了一组重要恒等式,由此可以很好地解释顶点介数分布规律[8-9]
定理(顶点介数恒等式):连通无向简单网络中所有顶点介数之和约等于网络平均最短距离 ℓ 的 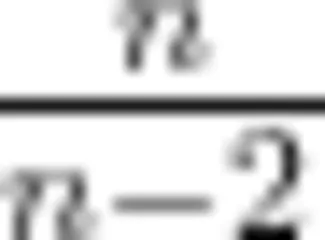 倍减去1,即
倍减去1,即
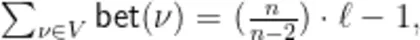
式中: ℓ 表示网络的平均最短距离, 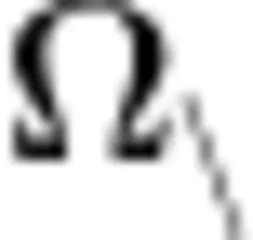 为网络中顶点个数。
为网络中顶点个数。
证明:由于网络中顶点 ν 的介数定义如下
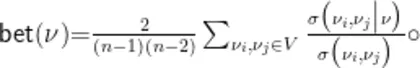
本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:gjxk20251306.pd原版全文