“专创融合"理念下高等数学教学改革探索

中图分类号：G642 文献标志码：A 文章编号：2096-000X（2025）13-0078-04

Abstract：Inordertoimplementtheeducationalpolicyof"innovationandentrepreneurship"，startbusinesesandmake inovations，theAdvancedMathematicsouseistakenasthecarier，anditisintegratedwithinnovativeandentrepreneurial elements，and the integrateteaching mode of "professional" + "innovation and entrepreneurship" is explored.Based on the teaching contentfAdvancedMathematics，guidedbythelatestinnovativeandentrepreneurialthinking，withtheintegrationof" professional" + "innovationandentrepreneurship"asthegoal，andtaking "likesaltinto water，likespringinflowers"asthe standard，wewillsteadilypromotetheteachingreformofAdvancedMathematicswiththeintegrationof "professional" + "innovation and entrepreneurship".

Keywords：AdvancedMathematics；innovationandentrepreneurshipeducation；teachingreform；innovativethinking; entrepreneurial consciousness

习近平总书记在二十大报告中指出：“教育、科技、人才是全面建设社会主义现代化国家的基础性、战略性支撑我们要坚持教育优先发展、科技自立自强、人才引领驱动，加快建设教育强国、科技强国、人才强国，坚持为党育人、为国育才，全面提高人才自主培养质量，着力造就拔尖创新人才，聚天下英才而用之。""必须坚持守正创新…守正才能不迷失方向、不犯颠覆性错误，创新才能把握时代、引领时代。"国家将育人与创新提升到了新的战略高度，从侧面说明了其重要性和急迫性，而高校是培养高素质人才的主阵地，应该承担起这样的历史使命和重大责任。

长期以来，大学生专业教育与“双创"教育面临孤岛困境，往往是“两张皮”，不能相互融通。如何打破两者相互隔绝的困境，如何在课堂教学全过程、全方位、全员之中融入“双创”理念，推动两者同向同行，构筑育人大格局，是新时代高校面临的重要挑战。如何贯彻"课程承载双创"和“双创寓于课程”的理念是我们每一个教学工作者应该考虑的首要问题。作为一名一线的高等数学教师，如何在高等数学课程教学中贯彻“双创”教育方针政策是高等数学课程教学改革中面临的一个新的问题，急需认真思考。

作为一门古老的学科，高等数学[2-3的概念、定理、性质中蕴含着丰富的思想、观点和方法，而且是面向大一新生开设的一门重要的基础课[4-，开课时间跨度大，课时量多，不管是从时间节点、时间跨度还是内容上来说，都具有与“双创"融合的优势[8]

为了贯彻“双创"教育方针政策，本文以高等数学课程为载体，将其与创新创业元素相融合，初步探索“专业” + “双创"融合的教学模式。以高等数学教学内容为立足点，以最新的创新创业思维为引领，以“专业” + “双创"融合为目标，以“如盐人水，如春在花”为标准，扎实推进“专业” + “双创"融合的高等数学教学改革，提升学生的科学素养，促进创新思维、创新能力、创新创业意识、决策能力的培养，深度挖掘学生的创新创业潜力，坚持守正创新，为培养创新型人才打下坚实的基础。

一函数概念

函数概念随着数学的发展而发展，在发展过程中不断地从具体到抽象、从特殊到一般，最终得到严谨化和精确化的表达。函数概念贯穿数学学习的始终，在初中阶段学生就接触到了函数，初中阶段从变量的角度给出了函数的定义。不难看出，初中课本中函数的定义是比较浅显的。随着学生学习的深入，认知水平的不断提高，以及集合概念的引入，高中阶段从集合间对应关系的角度刻画了两个变量之间的关系，进而给出函数的定义[10]。在大学阶段，学生接触到一个新的概念一一映射，于是从映射的角度给出函数的定义[2]。

对比初中、高中、大学这三个阶段函数的定义，不难发现，函数的定义由初中阶段描述变量之间简单的对应关系，到高中时期借助集合的观点给出定义，再到大学阶段将函数看作是一种特殊的映射，根据不同阶段学生的学习能力以及认知水平，由浅显到深入，逐步精确化。让学生查阅资料了解函数概念的发展史，体会函数概念在曲折中前进，事物的发展也是一样，往往不能一帆风顺，而是前进性与曲折性相统一。引导学生认识到学习与创业也是一样，不能一蹴而就，而是一个循序渐进、逐步深化的过程，要用动态的、发展的眼光看待事物，这是一个创业者必须具备的素质。

函数概念逐步精确化的过程本质上也是一种创新，让学生领会并学习在函数概念发展过程中科学家们勇攀高峰、敢为人先的创新与奉献精神，鼓励他们在以后的学习中要发愤图强、传承科学精神，要有追求真理、探索未知、勇攀科学高峰的勇气和信心。

二一元函数、二元函数、多元函数

虽然一元函数、二元函数、多元函数的自变量个数不同，但是它们不管在理论部分，还是性质部分，都是极为相似的。因此，在学习这些函数的过程中，先学习一元函数的知识，熟练掌握一元函数的内容之后，再类比学习二元函数以及多元函数的知识就容易得多，且能更好地对比这些函数之间的异同。

由一元函数的概念发展到二元函数再到多元函数，本质上是一个创新的过程。由于一元函数只有一个自变量，在解决实际问题的过程中往往具有较大的局限性，因此将一元函数的定义域由一维空间推广成二维空间得到二元函数，进一步地将定义域推广成 n 维空间类比地给出多元函数，用于解决更为复杂的问题。这种由一到二再到多的创新过程是值得我们学习和深思的。在实际生活和创业过程中，经常会遇到一些问题，这些问题往往不是单一的，而是多个问题融合在一起的一个多元化的问题，因此可以参照一元函数发展到多元函数的这个过程，先去解决一个问题，然后找到这个问题和其他问题的共性或区别，再去解决其他的问题。一元函数到多元函数的创新，并没有推翻原有的理论、概念等，而是在原有的基础上又对其进行推广、丰富。创新并不意味着要完全推翻过去，也可以是对过去的重新编排和丰富。因此，在进行创新时，盲目地开始往往事倍功半，不仅耗费了大量的时间，创新出来的东西与原有的并无太大区别。教育学生要学会借鉴一元函数到多元函数的思想，进行“类比式"的创新，先研究原有物的特性，寻找出可以进行创新改进的地方，再在此基础上融入自己的新思想和新理念，既保留了事物本身的特性，又进行了创新。

我们在解决遇到的问题时，往往考虑的比较粗浅，只认识到某一方面的问题，却忽略了其他方面。一元函数到多元函数的演变启发我们在解决问题时，要有多元化的思维，从不同的角度入手去考虑问题解决的可能性，拓宽自己的解题思路，发散思维，举一反三，做到会解一道题就会解一类题，提升科学素养。发散思维的培养也是一种创新意识和创新思维的养成，注重创新思维和创新意识的培养才是从根本上落实创新，只有拥有这样的意识和思维，才能在实际生活中做到处处留心，处处创新。

三 导数、偏导数、方向导数

导数、偏导数、方向导数不仅是非常重要的数学工具，而且也蕴含着丰富的哲学思想和实践智慧，在学习它们的过程中，不仅要让学生理解其数学原理，更要理解和运用其背后的思想和智慧，来指导学习、生活和工作。

在研究一元函数的变化率时引入了导数的概念，对于二元以至于多元函数自变量不止一个，因此在研究它们的变化率时要比一元函数复杂得多，需要考虑关于其中一个自变量的变化率，于是引出了偏导数的定义。对于二元函数有两个偏导数，即关于 x 的偏导数和关于 y 的偏导数。如关于 x 的偏导数是让 y 固定不变，只让 x 发生变化时，考察函数变化率的问题。这就好比我们在解决问题时，固定其他条件不变，只改变一个因素，来观察问题的变化，从而找出解决问题的关键因素。这种方法在实际生活以及创新创业中也是常用的。事实上，无论在社会发展，还是在个人成长中，我们都不能一次性改变所有的因素，需要先固定大部分条件，然后改变一部分，观察结果的变化，从而确定最有效的改变策略。

偏导数刻画的是函数沿坐标轴方向的变化率，由于实际需要只考虑函数沿坐标轴方向的变化率是远远不够的，有必要探讨函数沿任一指定方向的变化率问题，由此引出方向导数。

从偏导数到方向导数的这种思想转变，实际上是一种从特殊到一般的认识过程，体现了辩证唯物主义的认识论，教育学生在认识世界的过程中要从具体的、特殊的事物开始，通过观察和实践，逐步抽象出普遍的规律，这种方法不论是在分析社会现象、处理问题还是在学习、生活、创业中都具有重要的指导意义。这种思想转变也体现了创新和全面发展的理念，在解决问题时不能只关注某一方面，而忽视了其他方面，要从全面的角度去考虑问题，这样才能发现更多的机会，把握住更多的可能性，同时也需要不断创新思维，突破传统的框架，开拓新的路径。在创业过程中，具备全面思考和创新思维的能力，对于发现新的商业机会以及制定有效的商业策略具有重要的作用。

四 定积分、反常积分

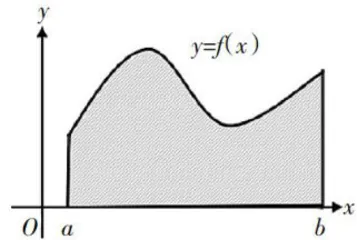
引入定积分概念时，通过问题驱动的方式，让学生思考如何求由连续曲线 y=f （ x ） （ f （ x ）⩾0 ） ， x 轴，以及两条直线 x = a ， x = b 围成的曲边梯形的面积，如图1所示，以此激发学生的兴趣、探索欲，避免学生的畏难情绪，引导学生借助现有的知识解决新问题，进而从问题解决过程中领会并提炼出解题步骤：分割、近似、求和，取极限。然后引导学生由实际问题自然而然地过渡到数学理论，进而给出定积分的概念。有了明确的定积分概念以后，再由理论回到求曲边梯形面积的问题，形成前后呼应，让学生认识到曲边梯形的面积可以用定积分 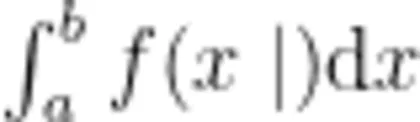来表示，由此揭示定积分的几何意义。这种由特殊到一般的思维也是在创新和创业过程中必须具备的素质。

掌握了定积分的概念以后，要让学生体会从实践中来，到实践中去，能够灵活运用定积分的知识去解决实际问题，充分认识到数学源于生活又服务于生活。进一步提出实际问题：设物体沿直线运动，其速度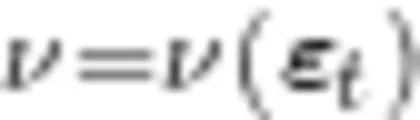 是时间间隔 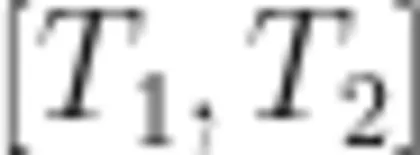上的连续函数， ν （ x ）⩾0 ，计算 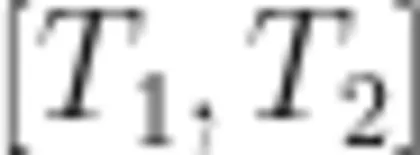时间内物体移动的位移。让学生独立自主地去解决这个问题，在解决问题的过程中提升分析问题和解决问题的能力，增强自主探究意识。