基于优化假设-演绎方法的流体力学课程教学改革探讨
作者: 廖斌 卜洋 汪超 陈善群中图分类号:0351.2 文献标志码:A 文章编号:2096-000X(2025)13-0141-04
Abstract:Basedonthetheoreticalframeworkandtechnicalroadmapoftheoptimizedhypothetical-deductivemethod, combinedwiththemasteryneedsofundergraduatesofmechanicalivilengineering,andothermajorsinFuidMechanicscourse, theteachingreformofFluidMechanicscoursewasdiscused.Specificallthediscussionwasonthreeaspets,ie.,heuseof empirical formulas,thedesignofexperimentalinstruction,andcomputersimulation.Moreover,twotypicalteachingcases,ie, theoreticalcalculationof liquidviscosityandnumerical simulationofdam-breakingwaterimpactstructuresweredesigned.These teachingcasespecifyhowtheoptimizedhypothetical-deductivemethodcanbeintegratedintotheteachingofanundergraduate fluid mechanics course.
Keywords:hypothetical-deductive method;Fluid Mechanics;teachingreform;teaching case; teaching innovation
流体力学是土木工程、交通工程、建筑环境与设备工程、城市地下空间工程、道路桥梁与渡河工程等诸多土建类专业的一门重要的学科基础课。该课程旨在为本科生提供流体力学方面的理论知识和实践技能,帮助本科生掌握流体力学的基本原理和应用,具有数学基础要求高、理论和实践紧密结合、应用广泛和知识面要求较广等特点。
基于多年的从教经验,我们发现土建类本科生在学习流体力学课程时往往会遇到以下几方面问题。① 理论公式推导不感兴趣。流体力学课程涉及的经典理论主要通过公式来表达,而这些理论公式的衍生发展均涉及大量的公式推导。而公式推导需具备高等数学、大学物理、理论力学等课程的知识储备和熟练运用,大部分本科生对此感到难度大且枯燥,从而表现出明显的缺乏兴趣及畏难情绪。 ② 经验公式运用不熟练。流体力学课程在工程实践的指导作用主要通过经验公式来实现,经验公式的使用场景和适用条件尤为重要,使用不当会对工程实践产生较大影响。而部分本科生对经验公式的运用存在混淆使用场景及不熟悉适用条件等问题。 ③ 概念理解不透彻。对大学一二年级只接触固体力学的本科生而言,刚开始接触流体力学时遇到的一些概念,如流体微团、连续介质假设、欧拉法和流迹线等均是全新且抽象的。大部分本科生对这些概念感到晦涩难懂,难以理解。 ④ 实验参与度不高。鉴于流体力学课程课时压缩导致实验课时减少,再加上实践教学的分数占比不高及实验设备台套数不足等因素,使得本科生实验参与度普遍不高。大部分学生未能从实验教学中实现理论验证、公式运用、现象理解等学习目的。 ⑤ 计算机仿真模拟未涉及。计算机仿真模拟是流体力学课程教学的重要辅助手段,它与实验教学可相互补充,一定程度地解决实验条件不足的问题并帮助本科生理解流体力学概念、熟悉经验公式。但稍显遗憾的是,目前大部分高校在讲授流体力学课程时并不涉及计算仿真模拟,使得大部分本科生对计算机仿真模拟完全陌生。
针对以上问题,这里拟引入假设-演绎方法对流体力学课程教学进行一定的改革探讨,并拟通过经验公式使用、实验教学设计及计算机仿真模拟等方面的教学案例来深入探讨假设-演绎方法在流体力学课程教学改革中的适用性。本文的教学改革探讨有望提升流体力学课程教学质量,激发学生的学习热情,为本科生掌握扎实的流体力学知识助力。
一假设-演绎方法
根据Popper[1-3]及后来研究者[4-5的观点,假设-演绎方法(hypothetico-deductive method,简称H-D method)是一种可以广泛用于各学科领域科学探究的普适性经典方法,它的核心思想包括以下七个步骤: ① 确定广泛的问题领域; ② 确定问题陈述; ③ 提出假设; ④ 确定措施; ⑤ 数据收集; ⑥ 数据分析; ⑦ 数据解释。
不难看出,根据该方法,科学探究的过程是以可证伪的形式提出假说,在结果尚未可知的情况下对可观察到的数据进行检验。如果实验结果可能而且确实与假设的预测相反,则被认为是对假设的证伪。如果测试结果可能与假说相反,但并不违背假说,则证明了理论。
为将假设-演绎方法更好地融入流体力学教学改革,同时更加贴合流体力学课程理论与实践紧密结合的特点,我们将假设-演绎方法的核心步骤做了一定的优化。优化后的步骤具体如下: ① 与初步表述、问题识别相关的观察和提问; ② 理论框架、背景研究、初步信息收集; ③ 提出假设(可检验、可证伪的假设); ④ 定义、设计测试实验; ⑤ 与实验经验相关的结果预测;⑥ 实验、数据记录和收集及分析/解释; ⑦ 假设和预测的验证或失效及其评估; ⑧ 在可靠验证的基础上形成理论或定律。
优化后的假设-演绎方法技术路线示意图如图1所示。
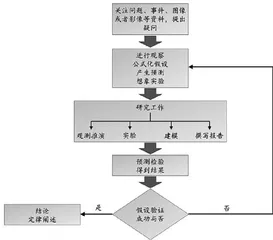
本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:gjxk20251333.pd原版全文
二流体力学课程教学改革探讨
现有的高等教育课堂上的本科生是一个更加多样化、与社会联系更紧密、会处理多项任务和精通技术的学生群体。与上一代学生相比,这一代学生的学习机制已经从传统的被动式学习转变为更多的动手操作和主动式学习[6-7。基于优化假设-演绎方法的理论框架及技术路线,结合机械类、土木类等专业本科生对流体力学课程的掌握需求,这里对流体力学课程教学改革提出几点探讨。
要求学生利用课余时间理解掌握一些流体力学基础定律定理,例如牛顿第二运动定律、斯托克斯定律、阿基米德定律和完全流体的伯努利原理等,并推导演绎诸如黏度和阻力的一些概念及参数,例如雷诺数、物体在空气中的自由落体的末期速度、物体在水/油中下落的末期速度等。在自主学习以上知识的过程中将所有学习内容做好笔记,以随时翻阅并修改补充。同时,学生还可就以上知识提出疑问、拓展思路,并与同学及老师积极讨论。
要求学生在课余时间设想一些相对简单的廉价实验,确定并强调相关的科学概念和观念,加深他们对这些科学概念及观念的理解。以下是可供参考的,利用简单材料实现的一些实验项目(括号内容是这些项目对应的流体力学知识): ① 伽利略的物体下落实验,使用运动球体在空气中从相同高度下落,观察不同直径、密度球体的末期速度差异; ② 制作经典的笛卡尔潜水器(了解压力、阿基米德浮力); ③ 用布料和绳子制作降落伞; ④ 观察沙砾在水中的沉降; ⑤ 观察气泡在油或水中上升,或高尔夫球在水中下落(黏度计算); ⑥ 伽利略的斜面滚球实验(重力计算); ⑦ 乒兵球的悬浮(科恩达效应伯努利方程); ⑧ 根据阿基米德定律测量物体的密度(软木塞、铅块等)。
要求学生自行组成团队,选择一些感兴趣的流体力学相关的知识点,并借助计算机和网络资源、教科书、讲义、科学文章、练习和教学视频来实施基于所选择知识的假设-演绎方法,旨在提升学生的流体力学学识水平和培养学生的科学教育技能。
具体的实施内容主要包括: ① 组织学生团队进行互动式教学,获得反思性实践和科学质疑; ② 指引学生团队解决问题,提出并验证假设、理论或定律,设计相应的实验或者数值模拟模型; ③ 指导学生团队分析和理解科学现象,学习高效的测量和计算,完成实验数据记录的分析/解释; ④ 指导学生团队对验证假设进行评估,并在可靠验证的基础上形成理论或定律。
三 教学案例分析
(1) 液体黏度理论计算
一般认为,从装有环境液体(水或油)的垂直管子底部释放的小尺寸气泡(直径小于 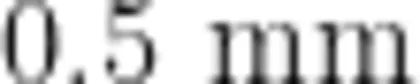 )会在很短的距离内达到其末期速度。此时只需通过测量从指定位置经过的时间,可以较容易地计算出小气泡上升的末期速度。由于气泡尺寸较小,在环境液体中上升过程中保持近似球形,我们可根据牛顿第二运动定律,列出小尺寸气泡所受外力(重量、浮力和阻力)的平衡方程式来估算出环境液体的黏度。以上做法符合斯托克斯定律(适用于小雷诺数条件)。
)会在很短的距离内达到其末期速度。此时只需通过测量从指定位置经过的时间,可以较容易地计算出小气泡上升的末期速度。由于气泡尺寸较小,在环境液体中上升过程中保持近似球形,我们可根据牛顿第二运动定律,列出小尺寸气泡所受外力(重量、浮力和阻力)的平衡方程式来估算出环境液体的黏度。以上做法符合斯托克斯定律(适用于小雷诺数条件)。
简单阐述就是通过小尺寸气泡在环境液体中的上升来计算环境液体黏度的关键步骤与对应的公式。首先,将小尺寸气泡看作一球形物体,根据牛顿第二运动定律,气泡在环境流体中的上升过程时,满足以下运动方程
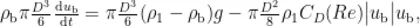
式中: D 为气泡直径; 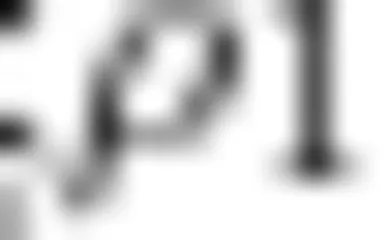 与
与 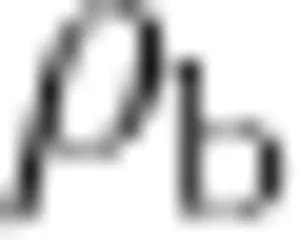 分别为环境液体及气泡的密度; R e 为雷诺数;
分别为环境液体及气泡的密度; R e 为雷诺数; 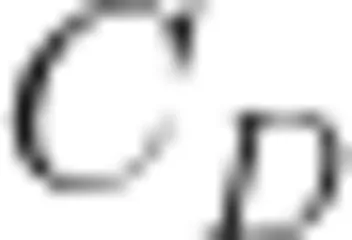 为与 R e 函数相关的阻力系数,根据斯托克斯定律,
为与 R e 函数相关的阻力系数,根据斯托克斯定律, 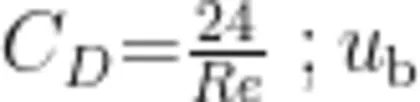 为气泡上升速度。
为气泡上升速度。
当气泡受力达到平衡( 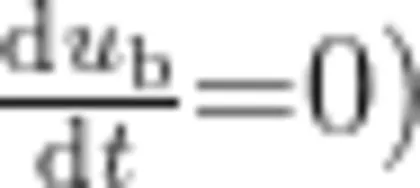 ,即气泡所受的浮力及阻力相等时,气泡达到末期速度,此时
,即气泡所受的浮力及阻力相等时,气泡达到末期速度,此时
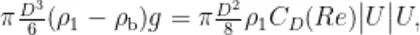
式中: U 为气泡上升的末期速度。
最终,小尺寸气泡上升的末期速度 U 的求解表达式为
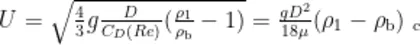
由式(3)可知,环境液体的黏度为
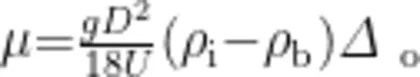
在通过小尺寸气泡上升的末期速度计算环境液体黏度的基础上,我们可以提出一个假设:具体将研究对象由小尺寸气泡改变为较大尺寸气泡,在气泡形状不是近似球形及不满足斯托克斯定律的条件下,如何通过较大尺寸气泡上升的末期速度计算环境液体黏度。这里可以指导学生对于较大尺寸气泡在不适用于斯托克斯定律的前提下,可采用其他阻力系数定律,例如席勒-诺曼定律来计算环境液体黏度。需要说明的是,计算过程中需要试错及迭代求解。
本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:gjxk20251333.pd原版全文