高等数学思政教学设计案例研究
作者: 蒋君 徐树立 刘云冰中图分类号:G642.0 文献标志码:A 文章编号:2096-000X(2025)13-0189-04
DOI:10.19980/j.CN23-1593/G4.2025.13.044
Abstract: Thispaper explores theteachingofideologicaland poltical cases in AdvancedMathematicscourse basedonthe guidingieologyofthesamedirectionandbehaviorofideologicalandpoliticalcourses,andthecharactersticsofWuhan UniversityofScienceandTechnology'sAdvancedMathematicscoursesand students.Takinggradientcontentasanexample,this paperprovidesadetailedintroductiontohowtoefectivelyrefinevariousteachingprocesessuchaspreclasspreparationcourse introduction,interpretationofconceptsandproperties,xampleanalysis,nowledgeexpansion,andpostclassgoupexercises.The studyintegratesideologicalandpoliticalelementssuchassaltintowaterintotheknowledgepointsofgradients,andguides studentstousemathematicalthinkingandmethodstosolvepracticalproblems,inordertoachievetheteachinggoalof cultivatingmoralityandtalent.Practicehasshownthatafterincorporatingideologicalandpoliticalcontent,thecoursecontent becomesmorerichandvivid,improvingtheteachingabilityofteachersandenhancingthelearninginterestofstudents.The communicationbetween teachersandstudentsismoreharmonious,andstudentsaremorewiling tothinkandhave thecourage to practice. The teaching effect has been greatly improved.
Keywords:curriculumideologicalandpoliticaleducation;AdvancedMathematics;instructionaldesign;casestudies;gradient
课程思政指以构建全员、全程、全课程育人格局的形式将各类课程与思想政治理论课同向同行,形成协同效应,把“立德树人”作为教育的根本任务的一种综合教育理念。课程思政主要形式是将思想政治教育元素,包括思想政治教育的理论知识、价值理念及精神追求等融入到各门课程中去,潜移默化地对学生的思想意识、行为举止产生影响。课程思政建设是构建全课程育人的格局,强化各类课程的育人功能,是高校思想政治教育的创新模式。
习近平总书记在党的二十大报告中强调“办好人民满意的教育”,对“全面贯彻党的教育方针,落实立德树人根本任务,培养德智体美劳全面发展的社会主义建设者和接班人"提出更高的要求。
高等数学是一门公共基础必修课,面向理科、工科、经管类等专业一年级的学生。高等数学包含一元微积分、多元微积分、空间解析几何、微分方程和无穷级数等内容,具有高度的抽象性、严密的逻辑性和广泛的应用性。
武汉科技大学(以下简称“我校"高等数学课程思政教学建设依托省级教学名师、省级精品课程、省级重点实验室,充分发挥校级支部工作室引领作用、师生主体作用,通过课程教学,让学生具备高等数学知识、运算技能,解决实际问题的综合能力。
将教学目标基于学情,启于课程,立足专业,在教授学生基础知识的同时,融入了科学认知意识、唯物辩证观的培养,在教授学生运用高数方法解决实际问题的同时,融入了数学建模、科学决策等专业素养的培养,同时在教学中厚植家国情怀,培养学生正确的三观和科技报国的使命感。根据教学内容的不同形式分别融入思政内容,如数学文化、哲学思想、学科发展、中国故事、逻辑推理、专题研究、生活实例和学科前沿等,以达到科学精神、唯物辩证、科学认知、文化自信、数学素养、责任意识、数学建模和科技强国等育人目标。
下面以梯度为例给出详细的思政教学设计案例教学设计。
一学情分析
梯度是《高等数学(下)》第9章多元函数微分学及其应用的内容,在学习梯度内容之前,学生已掌握了多元函数、偏导数、全微分和方向导数等知识。教材是由武汉科技大学数学与统计系数学教师陈贵词、余胜春主编的《高等数学(第二版)(下)》4。通过学习,让学生理解梯度的概念、梯度与方向导数的关系,了解梯度的几何意义,掌握梯度的计算方法,了解梯度的应用,本节课的教学内容与目标见表1。

本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:gjxk20251344.pd原版全文
二 教学设计
(1) 课前准备
课前学习群里布置预习问题: ① 寻求热锅上蚂蚁的最佳逃跑方向。 ② 查阅哈密顿算子应用和哈密顿的趣闻、趣事。并在学习群里分享学生们的优秀解答。
思政融入:通过问题锻炼学生思考能力,通过应用实例让学生感受数学的作用,通过科学家的趣闻趣事让学生感受数学魅力,提升学生的学习兴趣。
(二) 课程导入
方向导数计算公式回顾。
如果二元函数 f ( x , y ) 在点 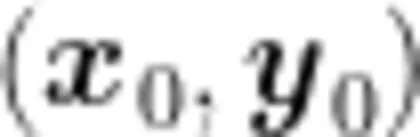 可微,向量 ι 的方向角为α,β,则方向导数
可微,向量 ι 的方向角为α,β,则方向导数 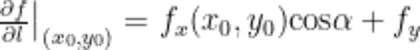
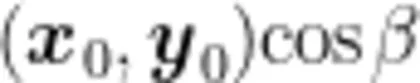 。令向量
。令向量 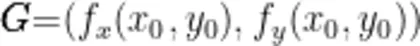 ,向量
,向量 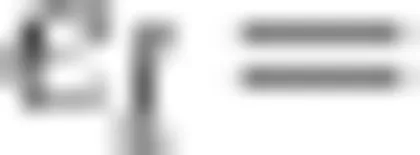 (cosα,cosB),则方向导数有新的计算方式:f
(cosα,cosB),则方向导数有新的计算方式:f 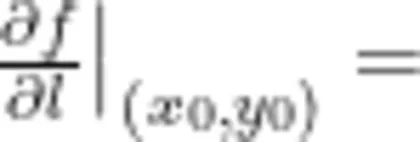
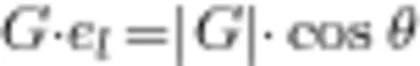 其中
其中 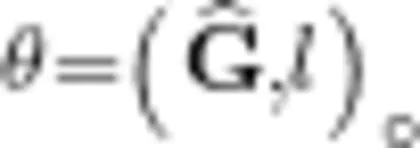 发现,当 ι 与 G 方向一致时,点(xo,yo)处的方向导数
发现,当 ι 与 G 方向一致时,点(xo,yo)处的方向导数 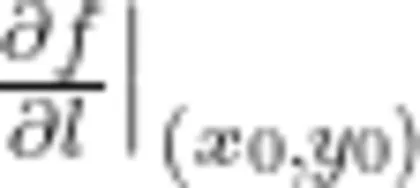 取得最大值
取得最大值 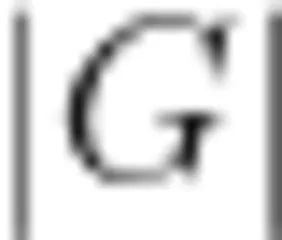 。
。
于是,定义的向量 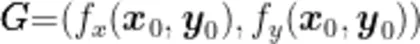 是一个这样的向量: G 的大小是函数 f ( x , y ) 在点
是一个这样的向量: G 的大小是函数 f ( x , y ) 在点 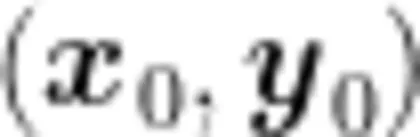 处最大变化率之值, G 的方向是函数 f ( x , y ) 在点
处最大变化率之值, G 的方向是函数 f ( x , y ) 在点 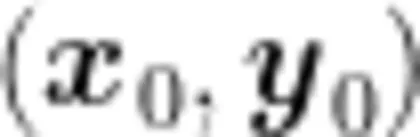 处变化率最大的方向。
处变化率最大的方向。
思政融人:把方向导数的计算公式用新的方式,即向量点乘表示,通过判断向量 ι 的方向,可以得到函数f ( x , y ) 在点 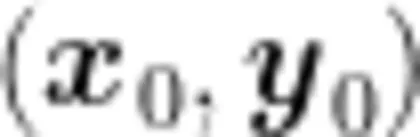 处的最大变化率。启发学生能够从多个角度思考问题,全面分析问题,即培养学生多角度思维,辩证唯物观。
处的最大变化率。启发学生能够从多个角度思考问题,全面分析问题,即培养学生多角度思维,辩证唯物观。
(三) 梯度概念
设函数 z = f ( x , y ) 在平面区域 D 内具有一阶连续偏导数,则对于每一点 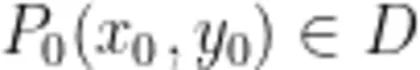 ,都可确定一个向量
,都可确定一个向量 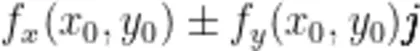 ,该向量称为函数 f ( x , y ) 在点
,该向量称为函数 f ( x , y ) 在点 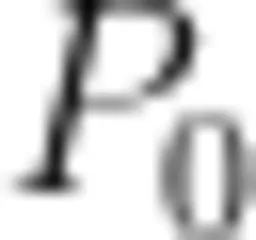
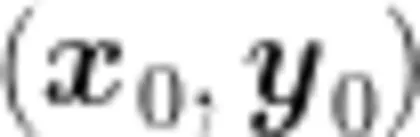 的梯度,记为
的梯度,记为 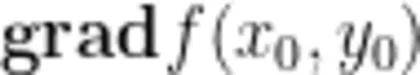 或
或 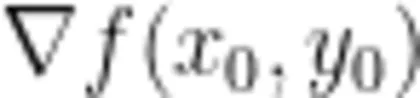 ,即
,即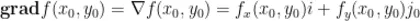
梯度的概念可以类似地推广到三元函数的情形。设函数 f ( x , y , z ) 在空间区域 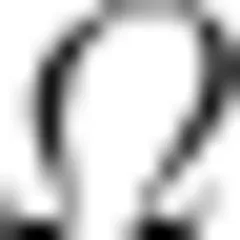 内具有一阶连续偏导数,则对于每一点
内具有一阶连续偏导数,则对于每一点 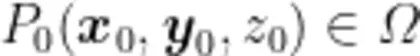 ,都可确定一个向量
,都可确定一个向量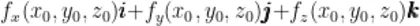 ,该向量称为函数 f ( x , y , z ) 在点
,该向量称为函数 f ( x , y , z ) 在点 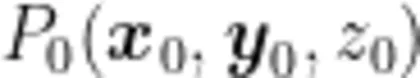 的梯度,记为
的梯度,记为 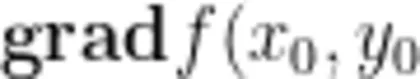
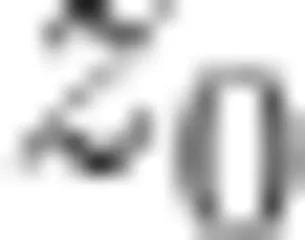 或
或 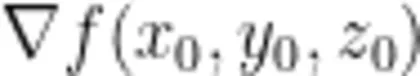 ,即
,即
本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:gjxk20251344.pd原版全文