小学数学练习课结构化设计策略

布鲁纳说过，与其说使学生掌握学科的基本事实和技巧，不如说是传播和学习结构。他认为，学生学习和掌握学科结构可以较容易地理解和掌握整个学科，因为理解基本的原理和结构的意义不仅适合学习特定的事物，还适合理解可能遇见的其他类似事物的模式。这就启发我们，教学设计要突出整体、结构的功能。《义务教育数学课程标准（2022年版）》明确提出了结构化设计的要求，并在“教学建议"中强调：“在教学中要重视对教学内容的整体分析，帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系。"练习课在小学数学课堂教学中占有较大的比重，一般一节新授课后就紧跟一节练习课。可见，小学数学练习课结构化设计是实现数学结构化教学的重要途径之一。下面，笔者以人教版小学数学教材四年级下册“三角形的三边关系练习课”为例，谈谈如何在练习课教学中展开结构化设计，帮助学生建立结构化的数学知识结构，实现数学知识、思维方式和解题策略的结构化。

一、创编关联习题，助力知识结构化

学生获得的知识、形成的技能，如果没有完整的结构把它们联系在一起，那是一种多半会被遗忘的知识和技能。学习的实质是学生认知的组织和重新组织，组织和重新组织的过程就是新旧知识相互联系、相互作用的过程。因此，在练习课教学中，要实现有意义的学习，教师要关注数学习题之间的关联，即用整体视角考察相关的练习资源，利用相同主题不同习题和不同主题相似习题之间的内在联系，多维度审视、创编和建构，形成结构化的知识体系。当完成新课教学之后，教师应对教材中编排的练习进行适当的梳理、分析和关联，整体创编关联习题，展开结构化练习课设计。

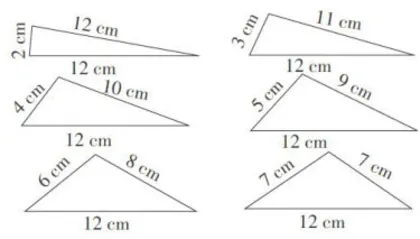
【改编基础题】图1中哪组线段可以围成三角形，为什么？

本题是“三角形"单元练习十五第6题的改编题（原题是：在能围成三角形的各组小棒下面画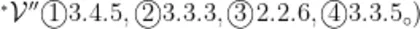 ，其目的是激活学生已有认知，让学生解释“能否围成三角形的道理”，在观察、思辩、交流等活动中提高解决问题的能力，发展推理能力和空间观念，同时为后续深度学习积累素材。在教学时，教师先让学生通过观察每组中三条线段的长度，运用“三角形两短边之和大于第三边”来判断能否围成三角形。接着，教师引导学生观察“围成的两个三角形之间有什么联系”，从而让学生发现：两个三角形的周长相等，最长边和两短边之和也相等。然后，进一步引导学生在计算周长的过程中发现：三角形的周长可以分成“最长边"和"两短边之和"两个部分。

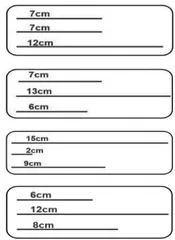
【原创发展题】最长边是 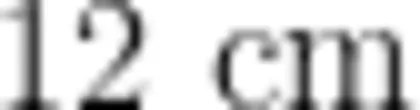，两短边之和是 1 4 c m 的三角形还有哪些？

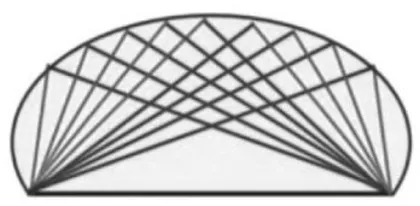
本题主要引导学生采用“固定最长边不变，把两短边之和分成两部分”的方法来解决实际问题（如图2）。接着，教师引导学生借助想象“把这些三角形都画在一起会是怎样的图形”，并借助视频播放把这些三角形画在一起形成美丽的建筑模型的动态过程（如图3、图4），以促进学生的空间观念和几何直观的发展，让学生体验数学的价值，感受数学的美。

【改编拓展题】把一根 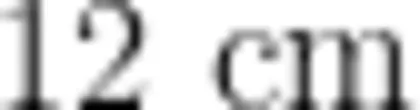长的小棒剪成3段（每段长为整数），哪几种剪法能围成三角形？（接头处长度忽略不计）

本题学生的错误率较高，而且答对答案的学生几乎都是猜出来的。在教学时，教师要鼓励学生注重练习反馈交流，引导学生有序思考，并运用已有经验迁移，在优化思考方法的活动中构建解决此类问题的一般模型：先把三角形周长分成两部分“最长边"和"两短边之和”，再把"两短边之和分成两部分”。

“三角形三边关系"的教学大多局限于发现三角形的三边关系，并运用三边关系判断三条线段能否围成三角形。这样不利于学生建构有关三角形边的结构化认知，也不利于学生高阶思维的发展。在“三角形的三边关系练习课"教学中，基于学生的已有知识经验，教师抓住各习题之间的内在联系，创编了3道相互关联的习题，让学生经历理解与迁移、联结与拓展、实践与应用的建构过程，从而进一步加深对“三角形任意两边之和大于第三边"的理解，形成内在联系紧密、具有广泛迁移价值的认知结构。

二、融通活动经验，促进思维结构化

融通是指借助新旧活动经验之间的联系，将新的思维经验纳入已有的思维经验，帮助学生在对比、重组、改造中不断丰富原有的经验，达到把“相同”与“变异"的思维经验构成一个整体，进而使学生从“单一割裂的碎片化思维"向“整体融合的结构化思维"转变。

在教学“三角形三边关系的练习课”时，教师可以组织三个片段的学习活动（如表1），帮助学生对零散的已有思维经验进行重组和整合，引导学生把习得的思维方法迁移到相似的学习活动中，促进思维的结构化。

教师以“围成的两个三角形之间有什么联系”为切入点，通过观察三角形各边的数据特点，引导学生发现三角形的周长可以分成“最长边"和“两短边之和”两个部分，接着通过两个跟进活动，把“三角形三边的关系、三角形的周长、三角形的最长边、三角形的两短边之和"等这些零散的知识经验进行重组和整合，引导学生将已有思维经验迁移到解决问题活动中，促进思维的再生长，从而提升知识应用和解决问题的能力，促进思维的结构化。

三、优化思考方法，构建策略结构化

数学是一门逻辑性较强的学科，很多学生在解决数学拓展题的过程中会遇到一定的困难，正确、合理、有结构的思考方法不仅能够帮助学生顺利地将数学题目解答出来，同时也有助于学生自主学习能力、思维能力和创新能力的提升。在数学练习课教学中，教师要提倡解决问题策略多样化，重视解题方法的优化，引导学生进行不同解题方法的系统关联，对核心的解题方法和解题策略进行提炼、归纳与应用，进而不断提升学生的结构化水平。

在解决“把一根 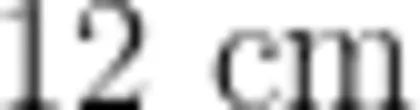长的小棒剪成3段（每段长为整数），哪几种剪法能围成三角形？"时，学生主要有两种典型思考方法：“固定第一条边"与“固定最长边”。在教学中，教师以“这两种方法有什么相同之处与不同之处？”为切入点引导学生展开交流。学生在观察、对比、交流中发现：方法一是把 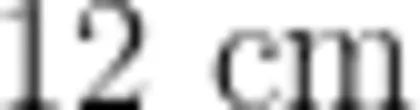长的边分成三部分，先确定第一条边，教学片段 方法表征 思维分析片段一师：仔细观察上图，围成的两个三角形之间有什么 学生在讨论“围成的两个联系？ 三角形之间有什么联系”的活生：最长边都是12 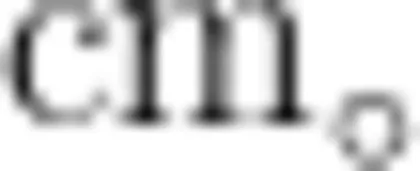（204号 周长 动中，将已有的思维经验进行生：两条短边之和都是 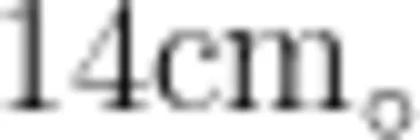（204号重组与整合，发现了“三角形生：两个三角形的周长都是 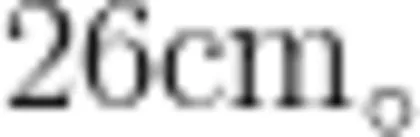两短边之和>最长边 的周长 Σ= Σ 最长边 + 两短边之师：你是怎样发现的？和”，为利用“三角形三边关生 ： 7 + 7 + 1 2 = 2 6 ， 6 + 8 + 1 2 = 2 6 ° 生：两个三角形的最长边都是 1 2 c m ，两短边之和 系”解决拓展练习题做好准都是1 4 c m， 1 2 + 1 4 = 2 6 ° 备。师：看来三角形的周长可以分成“最长边"和"两短边之和”两部分。片段二12cm、1cm、13cm问题情境：像这样最长边是 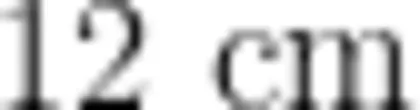，两短边之 12cm、2cm、12cm 学生在独立思考、交流汇

和是 1 4 c m 的三角形还有哪些？ 12cm、4cm、10cm 报等活动中，将已有活动经验生：最长边 1 2 c m ，第二条边可以是 1 c m 第三条边 12cm、5cm、9om进行重组与整合，创造了“最就是 1 3 c m； 接下来最长边还是 1 2 c m ，第二条 12cm、7cm、7cm长边固定不变，把两短边之和生：边按边序是 边按顺序是2厘米，第三条边就是 第三条变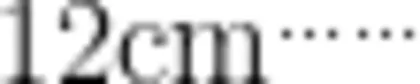， ，和 最边：2m.7cm 分成两边”的解题方法，促进 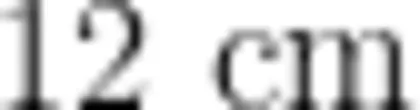，固定不变，两短边之和是 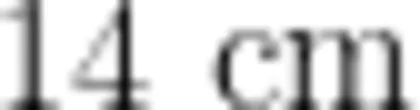，14可以分成5和9、4和10、3和 26cm、8cm 了思维的生长。④4cm、10cm11、2和12，有4个三角形。 12cm 53cm、11cm⑥2cm、12cm片段三问题情境：把一根 1 2 c m 长的小棒剪成3段（每段长为整厘米数），哪几种剪法能围成三角形？ 1、1、10× 2、2、8 × 3、3、6× 4、4、41、2、9 x 2、3、生：假设第一条边是 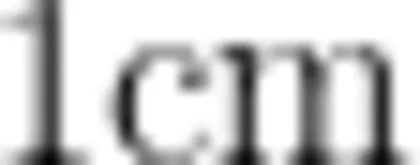，第二条边也是 1 c m 第 3、8 × 2、4、6×7 × 2、5、5三条边就是 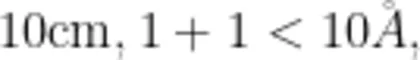不能围成三角形； 6X 学生在独立思考、记录方第一条边还是 1 c m ，第二条边按顺序是2 ： c m 法、交流汇报等活动中，再一第三条边就是9 c m ，也不能围成三角形… 1 次将已有的活动经验进行重生：设第一是 那么11有5种分法，每种分法都不能围成三 ∣ c m， 剩下务边之和能 1 1 c m 1 组与整合，已，有活动验定角形；假设第一条边是 2 c m ，剩下两边之和 X2AAA 第一边不变，把剩下的分成两是 1 0 c m ，那么10也有这样5种分法，其中2 c m. 部分”和“固定最长边不变，把5 c m， 5 c m 可以围成三角形…最长边：55cm、2cm 最长边：①4cm、4c 剩下的分成两条短边"等解题生：三个数中不可以出现6，因为其他两个数相加也是6了。假设最长边是5 c m ，第二条边也是5cm，第三 24cm、3cm 方法，进一步理解了三角形的条边就是2 c m ；也可以是5 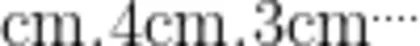三个数里不可以出现6，因为另外两个数相加也是6了。 三边关系，促进了思维的再生生：最长边最多是 5 c m ，两短边之和就是 7 c m ，那 2、5、5 长，实现了策略的结构化。么7可以分成5和2、4和3；最长边还可以是4 4、4、4

cm，两短边之和是 8 c m， 8 分成4和4。

再确定第二条边和第三条边，这样能够不重复、不遗漏地列举所有的剪法，有序又完整。但这种方法较麻烦，如果小棒的长度再加长，就比较费时；方法二是把 1 2 c m 先分成两部分，根据"三角形两短边之和大于最长边"先确定最长边的长度，再把剩下的分成两部分，既有序又简便，也更容易让人一眼看出有没有重复或遗漏。接着，教师通过问题“你能在方法一中找到‘最长边'和‘两短边之和'吗？"让学生在观察交流中找到了方法一中的“最长边"和“两短边之和”，并发现方法一中不能围成三角形的原因是“两短边之和小于或等于最长边”，“两短边之和大于最长边”的剪法才能围成三角形，打通了两种思考方法之间的联系，实现了解题方法的优化，提升了学生解决问题策略的结构化水平。

总之，小学数学练习课结构化设计是基于学科知识的逻辑结构和学生认知的整体建构的一种教学方式，是数学结构化教学的重要组成部分。在练习课结构化设计中，教师要以整体视角深入研读教材习题和各种相关资源，挖掘习题的知识本质，探寻习题之间的内在关联，帮助学生经历理解与迁移、联结与拓展、实践与应用的主动建构过程，实现数学知识、思维方式和解题策略的结构化，促进学生数学核心素养的提升。

（作者单位：浙江省温州市瓯海区实验小学）