在操作与想象中培养理性思维

思维是人脑对客观事物的本质属性与内在联系的概括的、间接的反映。而理性思维是一种有明确的思维方向，有充分的思维依据，能对事物或问题进行观察、比较、分析、综合、抽象与概括的一种思维，是人们以理性精神为根基，把握客观事物本质和规律的思维。在教学中，教师要充分关注并激发学生的理性思维，使其成为学生勇攀科学高峰的灯塔。《义务教育数学课程标准（2022年版）》明确指出，数学在形成人的理性思维、科学精神和促进个人智力发展中发挥着不可替代的作用。由此不难看出，培养并发展学生理性思维既满足学生数学学习的需要，更为学生未来高质量发展奠定了基石。

“"是人教版小学数学教材六年级下册的内容，圆柱是学生在一年级初步认识圆柱、五年级充分研究长方体和正方体的基础上学习的又一立体图形，为后续学习圆锥、球等立体图形奠定基础。在教学中，教师要以操作为手段，以活动为载体，引导学生经历圆柱特征的获得过程，感悟点、线、面、体之间的关系。

一、复习旧知，引入新课

[课件出示一年级所学的主题图（如图1）]

师：请看大屏幕！刚上一年级的时候，我们就初步认识了长方体、正方体、圆柱和球，五年级的时候我们又重点研究了长方体和正方体，请大家先回忆一下，长方体和正方体分别有哪些特征？

（学生回忆长方体和正方体的特征，教师适时板书“点、线、面”）

师：请大家再回忆一下，当时我们是用什么方法进行研究，从而得到这些特征的？

（结合学生回答，教师适时指出在研究长方体时用了观察、操作、比较、分析等方法）

师：除了研究长方体和正方体，你们还想研究这里面的哪些立体图形？

（学生各抒己见，教师适时引入新课，板书“"）

【思考】一年级刚入学时，学生的知识主要来自生活经验，能直观辨认出属于哪一种立体图形就行，培养的是感性思维。但随着年龄的增长、知识的积累，到了高年级，学生正式接触并研究长方体和正方体，学会从不同方面探索圆柱的特征，归纳探究方法。这样复习可以为探究圆柱的特征搭建“脚手架”，有助于发展学生的理性思维。

二、操作交流，探究特征

1.验证猜想，首探特征

（学生根据一年级所学的主题图及生活中的圆柱体，独立描述圆柱长什么样）

师：圆柱到底有哪些特征呢？接下来，我们就以小组为单位，从点、线、面的角度出发，运用观察、操作、比较、分析等方法来进行研究。请看活动要求！

活动要求：

（1）分一分：以小组为单位，组长分配好

学具框中的圆柱。（2）看一看：多角度观察圆柱的外形。（3）做一做：动手摸一摸、画一画、量一量，思考圆柱具有哪些特征。（4）说一说：组长组织交流各自的发现。

（学生分组研究，教师巡视，学生汇报交流）

生：圆柱上下底各有一个圆。

生：圆柱中间有一个侧面，是一个曲面。

师：圆柱底面上的两个圆有什么关系？

生：是两个完全相同的圆。

师：圆柱底面是两个完全相同的圆，这只是我们的猜想，还需要……

生：验证。

师：接下来，请大家以小组为单位，想办法验证这个猜想。

生：我们组用直尺测量了圆柱形木棒上下两个底面的直径，它们的直径长度都是5厘米，所以它们是两个完全相同的圆。

生：我们组先在白纸上沿着圆柱底面边线描出一个圆，再把圆柱另一个底面压在白纸上，发现它能与之前画的圆完全重合，说明这是两个完全相同的圆。

生：我们组把圆柱形胶棒的盖子拔下来，然后用它与胶棒的另一端比了比，发现它能与另一端的底面完全重合，所以这两个底面是完全相同的圆。

师：刚才大家通过量一量、画一画、比一比的方法验证了圆柱的底面是两个完全相同的圆，现在我们可以得出结论了吗？

生：可以。

师：同学们真棒！以后我们在学习过程中如果有了猜想，也可以按照这样的思路进行验证，最后下结论。

【思考】通过小组活动，学生快速发现圆柱有两个底面和一个侧面，但对于两个底面之间的关系，学生会凭着感觉认为它们是两个完全相同的圆，从理性思维的角度来说，这只是学生的一种猜想，教师适时引导学生通过小组合作，独立验证，从而最终发现这个猜想是正确的。“猜想一验证—结论"这样一个完整的探究过程，充分展示了数学思维的组织性和严谨性，点燃了学生科学探究征途上的理性思维之光。

2.自主对比，再获特征

（课件出示学校腰鼓队的腰鼓）

师：它是圆柱吗？你是怎么想的？

生：它不是圆柱。圆柱上下底面一样大（边说

边比画胶棒），而腰鼓的中间已经突出来了。

师：说得真好，圆柱从上到下是一样粗的，这也是圆柱的一个重要特征。

师：现在你们能判断出哪些图形是圆柱吗？（课件出示图2）

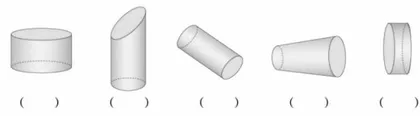
（学生快速判断，并说明判断依据）

【思考】腰鼓图片与学生脑海中的圆柱存在明显差异，学生猜想它不是圆柱。接着，他们用实物进行验证，最终准确判断腰鼓不是圆柱，并进一步归纳出圆柱应该是从上到下一样粗的。再次应用“猜想一验证一结论"这一理性思维探索新知，在获得圆柱新特征的同时，进一步提升了学生的空间想象力。

3.游戏引高，三探特征

课件出示游戏规则

游戏规则：1.选一选：全班选4名动手能力强的同学组成两队进行比赛。2.分一分：每队2人分工合作，1人递圆片，另1人叠圆片。3.叠一叠：把每次递来的1张圆片整齐地叠成一个圆柱。4.比一比：看哪一个小组20秒内叠的圆片最多。

（教师挑选4名学生进行比赛）

师：游戏结束了，你们觉得哪一队能获胜呢？为什么？

生：第一队获胜，因为他们叠的圆柱比第二队叠的高。

师：是的，一个小小的游戏让我们发现圆柱有高。（板书“高"）

师：到底什么是圆柱的高呢？请看！

（课件出示圆柱的高的定义，同桌之间指认圆柱的高，学生指高，并进一步发现圆柱有无数条高）

【思考】叠圆片游戏不但活跃了课堂气氛，而且将课堂的关注点无痕地引向了圆柱的高，进而引领学生去探究出圆柱有无数条高。同时让学生现场参与、观摩游戏的过程，亲眼见证一张张同样的圆片最后叠成了一个圆柱，这为后续“面动成体"的动态课件演示做了一个很好的铺垫，更有利于学生理解“面动成体”。

三、动态阐释，揭秘本质

1.卷移搭配，揭示本质

师：今天我们学习了这么多圆柱的特征，想不想亲手制作一个圆柱呢？请看活动要求。

活动要求：

1.分一分：两人一组，组长分发学具框中的A4纸并分发两种大小不同的圆片。2.做一做：两人合作，完成圆柱的制作。3.说一说：完成之后，小组内说一说自己是如何制作圆柱的。

（学生小组合作，动手操作，组内交流，全班汇报）

生：我们小组把长方形纸的长边卷起来，再配上两个大一点的圆做底面，就做成了一个圆柱。

生：我们小组把长方形纸的宽边卷起来，用两个小一点的圆做底面，也做成了一个圆柱。

师：卷成的这两个圆柱有什么相同点和不同点？

生：这两个圆柱大小不同，但侧面是同一张长方形纸。

生：把长方形的长边卷起来，长就是圆柱底面的周长；把宽边卷起来，宽就是圆柱底面的周长。

师：同学们观察得真仔细！是的，同一张长方形纸卷法不同，得到的圆柱也不相同，但它们的侧面都是完全相同的长方形。

师：如果只给你一张圆纸片，你有办法得到一个圆柱吗？

生：这个圆纸片本来就是一个圆柱。

师：你是怎么想的？

生：每一张圆纸片都是有厚度的，只是太薄了。

师：还有其他方法得到圆柱吗？（教师适时将手中圆纸片垂直向上平移）

生：圆纸片向上平移也可以形成一个圆柱。

师：你观察得真仔细！把一个圆垂直向上平移，它的运动痕迹可以看作一个圆柱。

（课件同步动态呈现）

师：刚才我们从静态视角研究了圆柱的特征，其实我们还可以从动态视角去解释圆柱为什么会具有这些特征。

师：请你从动态视角解释一下为什么圆柱底面是两个完全相同的圆。

生：这个圆柱是由同一张圆纸片向上垂直向上平移得到的，所以圆柱两个底面是完全相同的圆。

师：圆柱的侧面为什么是一个曲面，你能从动态视角解释一下吗？

生：圆柱的侧面是由同一个圆纸片垂直向上平移形成的，圆是一条封闭的曲线，由它形成的侧面就是一个曲面。

师：为什么圆柱从上到下一样粗，你能从动态视角解释一下吗？

生：同一张圆纸片垂直向上平移得到了圆柱，在平移过程中没有改变圆的大小，所以从上到下肯定是一样粗的。

【思考】学生通过把一张A4纸配合两张圆纸片做成一个圆柱的操作活动，充分感受“化平为曲”的神奇，为后续学习圆柱侧面积做好铺垫。随着难度的提升，一张圆纸片沿垂直方向平移留下的痕迹也能看成一个圆柱，教师辅以动画演示，帮助学生在头脑中刻上印迹形成表象，后续引导学生从动态视角理解圆柱所具有的本质特征就水到渠成了，学生的空间想象能力得到发展，理性思维也得到了进一步增强。

2.弃卷为转，动态提升

师：如果现在给你的还是一张A4纸，不用卷的方法，你能得到一个圆柱吗？

生：可以把这张长方形纸绕着它的一条边旋转，在旋转过程中就可以形成一个圆柱。

（教师现场演示以长方形的一条边为轴旋转形成一个圆柱）

师：以长方形的长边为轴旋转一周可以形成圆柱，长方形的长是圆柱的高，长方形的宽是圆柱的底面半径；同理，以长方形的宽边为轴旋转一周也可以形成圆柱，长方形的宽就是圆柱的高，长方形的长就变成了圆柱的底面半径，两种不同的旋转方式可以得到两种不同的圆柱。

师（小结）：以哪条边为轴，那条边就是圆柱的高。

【思考】一张A4纸除了用卷的方法，还可以通过旋转的方式得到一个圆柱。圆片平移的痕迹可以看成一个圆柱，这给学生打开了新的思路，让他们从中了解平面图形变成立体图形的奥秘。学生学习过的图形变换除了平移，还有旋转等。有了这样的知识储备及想象力，学生顺利找到了以长方形的一条边为轴进行旋转也可以得到圆柱的方法，进一步培养了学生的空间观念。

四、回顾总结，展望未来（略）

（作者单位：江苏省苏州高新区实验小学校新疆维吾尔自治区阿图什市昆山育才学校）