立足概念本质，发展学生数感

“数感”是指对于数与数量、数量关系及运算结果的直观感悟。数感不仅关乎学生对数的直观感知，更涉及学生理解和运用数解决实际问题的能力。如何在数的概念教学中发展学生的数感呢？老师教学“小数的意义"时，以正方形为学习素材，逆向设计，引导学生在正方形中表示一位小数、两位小数，初步理解小数的意义，感悟计数单位；同时依托学生作品，对比析疑、有效追问、精准点拨，直指小数概念本质，从而培养学生的数感。

【片段一】逆向设计，了解学生认知基础

师（出示任务一）：如图1，如果用正方形表示“1”，你能在正方形中表示出“0.3”吗？

师：这个任务有点难，我们要先弄懂问题，0.3到底在哪里？要弄懂这个问题要弄清楚1表示正方形面积的大小，0.3有多大，要怎么表示？先不要回答我的问题，有没有不懂的？如果不懂，哪里不懂？

生：正方形是一个图形，怎么表示一个数字呢？

师：他好像没有弄懂我们刚才讲的事情，1表示什么？

生：1表示正方形面积的大小。

师：所以0.3一定要在这个正方形里画出来。

【赏析】素养导向下的教学应从学生已有的知识经验和思维水平出发，根据学生数学学习的心理特征和认知规律设计教学活动。数是高度抽象的符号，小数的概念对于学生来说比较抽象。如何基于学生已有的整数学习的经验，让经验进入新的知识结构呢？任务一改变了以往看图写小数的顺向设计，变为根据小数来画图表示。这一逆向设计，有利于教师了解学生对核心概念的理解程度，并培养他们解决复杂学习任务的能力。王老师先让学生明晰任务的要求，确保学生理解任务一中的“1"表示正方形面积的大小，这是在正方形图形中表示0.3的基础。对于学生疑惑，教师不是直接讲解，而是引导学生自己理解，以扫除学生后续理解0.3的意义的障碍。

【片段二】对比析疑，理解一位小数意义

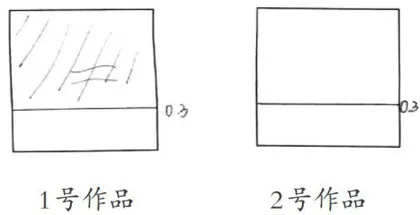
师（出示学生的1号作品和2号作品，如图2）：有没有发现，它们两个的线居然是在同一个地方。先不管对错，看看它们各要表达的0.3在哪里。

生（指着2号作品正方形的下面部分并涂上阴影）：我觉得这一个是对的。

师：为什么第一个不对？

生：如果把1分成10等份，一半是0.5，0.3比0.5少，所以是不对的。

师：听明白了吗？他用多少作为标准？生：0.5。

师：十等分以后，第一个作品对不对？

生（异口同声）：不对。

师：第二个作品有什么问题？

生：他出现的问题是，我们不知道他说的0.3是上面部分还是下面部分。

师：这种表示方法既不能表示上面部分，也不能表示下面部分。只能把这个点表示0.3。你觉得他为什么会这样表示？

生：他认为画0.3会比较精准。

生：我认为的0.3是指在这里（指着正方形右边的边上写着0.3的点）

师：对，这是一条数线，我们现在针对的是一条数线吗？

生：是面积。

师：对，是面积。所以，第二个作品对不对？生：不对。

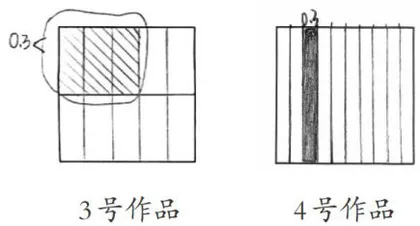
师：仔细观察图3中的3号作品和4号作品，它们都先做了什么事？

生：它们都把这个正方形分成了10等份。

师：它们的差别在哪里？哪个才是真正的0.3？

生：4号作品就只画了一格，所以它表示的是0.1。

师：听懂他在讲什么吗？但是他还是没有告诉我们为什么这个叫0.1。

生：因为4号作品分成10等份，只涂了1等份，10等份中的1等份就是0.1。

师：前提是这整个面积我们当成了多少？

生：当成1。

师：0.3怎么表示？（学生把4号作品涂了前两格，重新命名为5号作品，如图4所示）

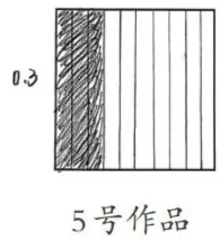
师：3号作品和5号作品为什么都可以叫0.3？他们画的方式都不一样。

生：因为都把1分成10等份，然后都涂了3份。师：听明白了吗？如果让你用分数表示0.3，你会用什么分数来表示？为什么会用这个分数来表示？

生： ○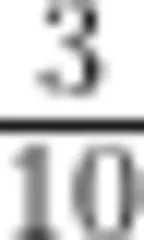

师： 表示0.3，为什么你想用它来表示？

生：因为都是平均分成10份，涂了3格，也就是取了其中的3份。

师：那4 呢？

生：0.4。

师：0.4怎么样？

生：0.4就是 。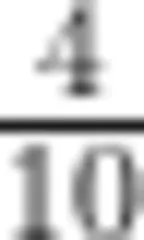

【赏析】学生拥有数感的主要表现包括：能够在真实的情境中理解数的意义，能用数表示物体的个数或事物的顺序。王老师进行三次对比反馈。第一次对比，辨析1号作品和2号作品能否表示0.3，明确1表示正方形的面积，0.3表示的是正方形的部分面积，而非线段长度。小数和整数一样，都是对数量的抽象表达，具有本质上的一致性。第二次对比，教师引导学生辨析3号作品和4号作品的差别，分析哪个才是真正的0.3。王老师引导学生深入思考，明晰0.3表示的是把正方形十等分后，10份中的3份而非第3份。接着，正确表征，进一步感悟了计数单位0.1和0.3的关系。第三次对比，教师引导学生辨析3号作品和5号作品为什么都可以叫0.3，为什么用 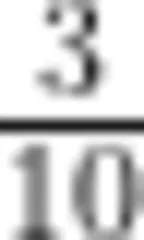表示0.3，引导学生理解一位小数的数学本质，同时厘清小数和十进分数的关系，直指小数的概念本质。在教学中，王老师根据学生对一位小数概念本质的认知层次选择相应的作品，由低到高进行对比辨析，不断指向理解一位小数概念的关键：平均分、十等分、份数。引导学生深入思考，让学生从模糊走向清晰，逐步构建起一位小数的意义，培养学生的小数量感。

【片段三】立足本质，聚焦小数计数单位

师：0.3会找了，你认为怎样表示0.37？如果用正方形表示“1”，你能在正方形中表示出0.37吗？（学生先独立思考完成作品，教师选出两份作品，如图5所示）

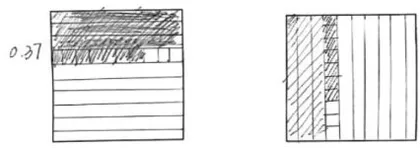
师：请你对比一下这两份作品，都是怎么画的？一次不要讲太多，我们用接力的方式一次说一个步骤。

生：先把正方形平均分成10行或10列。师：这个正方形用数字代表多少？生：1。师：也就是把1分成几份？生：10份。师：10份就是10行或10列对不对？好，那接着呢，到0.37了吗？生：接着就是涂出0.3。师：涂出0.3的时候要涂几个等份？生：涂3个等份。师：这里1个等份是多少？生：1个等份是0.1。师：这里有几个0.1？生：10个0.1。师：涂了几个0.1？生：涂了3个0.1。师：也就是多少？生：也就是0.3。

师：现在到了很重要的阶段。仔细看，他们在这两张图中都做了什么？生：都画出了完整的3大份和7小份。师：谁来补充一下？生：再把其中一个0.1平均分成10份。师：他说把谁分成10份？生：把其中的一个0.1平均分成10份。师：后来你看到了什么？平均分完10份之后就结束了吗？生：然后在10等份中再涂7份。师（指着后面的7格）：请问这里代表多少？生：0.07。师：什么叫作0.07？为什么这7格叫作0.07？生：因为他从0.1里面再平均分了10份，其中的7份，就是 0 . 0 7 。师：你没有真的回答出来我们的问题，谢谢你。你还差一点点，7个什么？生：把0.1分成10等份，所以每个等份就是0.01，7个等份就是 0 . 0 7 。

师：所以7个0.01就变成了多少？

生：0.07。

【赏析】史宁中教授认为，认识数整体是不变的，关键是抓两件事情，一个是个数，一个是计量单位。认识计数单位是一个由粗到细的过程，由多元到统一的过程。王老师引导学生理解两幅作品的0.37时，分两个层次来理解0.3和0.07的图形表征和含义。在任务二中，王老师再次强化学生对0.3含义的理解，加深学生对一位小数意义的理解；对0.07的理解，他通过问题，引导学生深入思考，感悟计数单位0.01和0.07的关系。计数单位的呈现，可以帮助学生更好地体会小数的产生就是对计数单位不断细分的过程，感悟小数部分相邻两个计数单位之间的关系。在整个思考过程中，学生进一步理解了小数的概念本质，培养了数感。

【片段四】大小关联，丰富数系认知结构

师：小数一定会在哪里？生：小数一定会在两个整数之间。师：他刚才表达那个很重要的点是什么？小数哪一部分是不到1的地方？比如2.4，哪里不到1？

生：零点四的部分不到1。师：请问这里的小数部分（指着黑板上的数的

小数部分）跟1来比，谁比较大？生：1大。师：9999.99的小数点后面的“99”有没有比1

大？生：没有，因为它只是小数，还没到1。师：那7.6怎么找？有点难哦。生：先找到7和8，中间分成10等份。师：分成10等份就找到7.6了吗？10等分之后呢？生：1份就是0.1，那就是6个0.1。师：所以我们要数到第几个点？生：数到第6个点。

【赏析】深度学习关注学科内容和学生学习的整体理解，让学生在理解知识本质的基础上进行自主构建。在教学中，王老师以问题引发学生深度思考，引导学生逐步感悟小数同整数一样都是用来计量数量的多少，都是一个个计数单位的累加。学生将小数与原有整数的认知体系进行联结，能形成新的认知结构。由此，学生的数感得到进一步发展。

（作者单位：广东省东莞市塘厦镇中心小学清华大学附属中学朝阳学校）