整合内容创设情境局部引导

一、活动目标与素养导向

经历“猜想 $$ 验证 $$ 证明”的完整探究过程，理解数学证明的必要性，明晰数学逻辑体系的基本框架；在直观理解和掌握图形与几何基本事实的基础上，经历得到和验证数学结论的过程，感悟具有传递性的数学逻辑，形成基于几何直观的推理能力；局部完善演绎体系，逐步规范几何推理与证明，强化数学语言表达，培养条理化表达素养。

二、教学重、难点

重点：构建数学逻辑体系的基本框架；通过局部完善的几何演绎体系，明晰知识的脉络，理解推理与证明的基础性、必要性和逻辑性，加强推理过程的准确性和严谨性。

难点：理解基本事实的意义和数学论证的逻辑，体会数学的严谨性，形成“重事实，讲道理"的科学精神，

三、教学片段

1.创设情境，引入新知

活动1师：同学们，上课之前，老师想给同学们做一个物理小实验。（教师做实验，实验效果如图1所示。）

营

师：你们看到了什么？

生：水里的筷子断开了。

师：请把筷子拿出来看看，真断了吗？生：两根筷子是好的。

师：再来考考同学们的数学观察力。

师：请看图2，线段 AB 与 CD 哪一条更长？

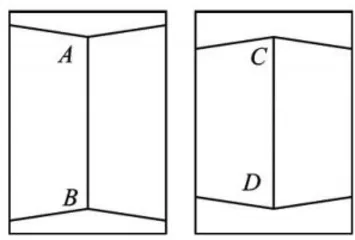
生： AB 长一些。

生：一样长。

师：那怎么去证实呢？

生：测量。

师：那就请你带上你需要的工具来判

断线段 AB 与 CD 哪一条更长。

师：通过度量线段 AB 与 CD 的长度，我们能证实这两条线段是一样长的。

活动2 师：请观察这两幅图，两条小道的面积相等吗？

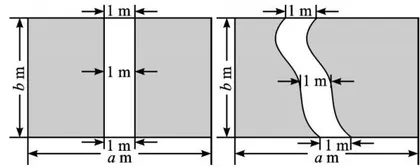
生：相等。

师：怎么证实？

生：可以把它两边的草坪拼接起来，然后再计算出草坪拼接后的面积。

师：那就请你上来移一移。如果平移后两个图形的面积是一样的，就代表中间这个小路的面积相同。那我们能不能计算出小路的面积呢？请同学们动笔算一下。

生：都是 bm² 。

师：通过平移和计算，我们都能证实这两条小道的面积是相等的。

活动3师：请同学们拿出研学单，动手操作，看用边长为 8cm 的正方形纸片能不能拼成长为 13cm 、宽为 5cm 的长方形纸片。可以互相交流。

生：可以。

师：请上台展示。

师：老师利用几何画板把这个重新拼合的过程也拼了一遍，拼完之后发现好像拼不成，中间有缝隙。为什么拼不成呢？又该怎么去证实呢？

生：我觉得可以算面积，师：大家顺着他的这个思路算算看。

生：正方形的面积是 64cm² ，长方形的面积是 65cm² 。所以面积不相等。

师：通过具体的计算，我们可以证实这个长方形是拼不成的。

师：老师刚刚带着同学们一起经历了三个活动，请问活动结束你有什么想法？

生：眼见不一定为实。

师：在日常生活中，观察，操作，甚至实验，确实能够帮助我们丰富对事物的认知，但有时候得到了一些结论，它们不一定是正确的，要想正确地去认识一件事情，还需要对此加以证明。这就是我们这节课要来一起探索的第12章的内容——证明。

2.从基本事实出发，探究新知

师：在参与活动的过程中，其实同学们已经对这三件事情做出了自己的判断。比如有同学判断线段 AB 与 CD 的长度相等，有同学说两条小道的面积是相等的，也有同学说这个长方形能拼成。那类似这样的三句话，都是在判断一件事情。在数学上，我们把判断一件事情的句子叫作命题。其实命题有很多，比如说今天是晴天、对顶角相等，等等。当然，我们需要提前明确研究对象，如知道“对顶角”的定义：两条相交直线所成的四个角中，有公共顶点且没有公共边的两个角称为对顶角。像这样，对名称或术语的含义进行描述或做出规定，就是给出它们的定义。你还能说出生活中或者数学上命题的例子吗？可以小组内交流。

生：平方等于4的数是2。

生：多边形的外角和是 360^∘ O生：2025年的2月有4个星期日。

师：我们一起来分析黑板上的刚刚三位同学说的三个命题。请同学们观察一下，从句子成分上看，它们有没有共同点？

生：这些句子都由两部分组成。

师：我们把前面这一部分叫作命题的条件，后面这一部分就是命题的结论。在数学中，我们规定，命题是由条件和结论两部分构成。那同位角相等的条件是什么？结论是什么？

生：条件是“两个角是同位角”，结论是“这两个角相等”。

师：“平方等于4的数是2”的条件是什么？结论是什么？

生：条件是“一个数的平方等于4”，结论是“这个数是2”。

师：这个命题做出的判断正确吗？

生：不正确。

师：如果条件成立，结论也成立，这样的命题叫作真命题。那如果条件成立了，推不出你想要的结论，这样的命题就叫作假命题。为什么能判断出“平方等于4的数是2”这个命题是假命题呢？

生：还有一个-2。

师：是的，要想证明一个命题是假命题，只需要举一个反例。2000多年前，古希腊的一个数学家对前人的一些数学成果进行了系统整理，并且把人们公认的一些真命题作为公理，用推理的方法，证实了一系列命题。像这样，根据已知的真命题，去确定某一个命题真假性的过程，就叫作证明。在第七章我们曾经获得过一个基本事实，即“同位角相等，两直线平行”。它的条件和结论分别是什么？

生：条件是“一条直线被两条直线所截，形成的同位角相等”，结论是“这两条直线平行”。

师：那你能不能从这个基本事实出发，证明这个新的命题一一垂直于同一条直线的两条直线平行？小组可以讨论一下。

师：请同学们一步步地说，尝试说出每一步的理由。

（学生积极发言，证明过程略。）

师：这样，我们就把这个命题有条理地证明出来了，也可以判断这个命题是一个真命题。我们把已经证明过的真命题又叫作定理。好，现在老师想请同学们回顾一下，从命题的给出到最后的证明，对于整个流程，你有哪些收获？

生：证明需要通过条件来推理。

生：可以从一个基本事实出发去证明。

师：同学们归纳得很好。下面请你观察"同位角相等，两直线平行"和"两直线平行，同位角相等"有什么区别。

生：条件和结论换了位置。

师：我们把这样的两个命题称为互逆命题。那第二个命题又该怎么证明呢？（教师介绍反证法并证明，证明过程略。）

3.师生小结（略）

四、教学反思

本章内容在学生数学思维发展进程中，起着从感性认知迈向理性分析的重要转折作用。在教学过程中，授课教师应确立单元整体教学目标，系统整合知识框架。对此，笔者在本节课中，设计了三个循序渐进的探究环节。

首先是情境导人。通过创设实际问题情境，探究证明的必要性。通过物理小实验，将学生熟悉的生活场景巧妙引人课堂，自然地引导学生基于生活现象展开数学思考，引发学生探究“为何要证明”，鼓励学生自主探究与合作学习。其次是新知探究。笔者系统梳理第12章的知识架构以及判断命题真假的方法，详细阐释定义、命题、定理、逆命题与互逆命题等核心概念，全面归纳判断命题真假的常用方法：（1）依据基本事实，正向推导命题；（2）通过举反例来判断；（3）反证法。同时，在课堂知识的生成过程中，笔者合理安排教学内容，设计多样化教学活动，引导学生总结证明与图形相关命题时的具体步骤：（1）依据题意准确绘制图形；（2）结合图形，根据命题的条件与结论，清晰写出已知与求证；（3）有条理地撰写证明过程。在探索过程中，笔者鼓励学生自主发现结论，丰富对数学知识的认知；在证明过程中，笔者引导学生证实结论，逐步学会如何逻辑清晰、条理分明地思考，强化了知识点的回顾，构建了结构化思维导图。

整堂课以“提出问题、动手实践、小组研讨、归纳总结、形成方法、具体应用"的流程展开，凸显了学生的主体地位，笔者则成为课堂的组织者、引导者以及学生学习的合作伙伴。在整个教学过程中，笔者持续鼓励学生积极思考，大胆表达个人见解，同时注重培养学生的探究意识以及与人合作、交流、分享的能力与精神，促进学生真正成为课堂的主人。

（该课例荣获2023年5月镇江市初中数学优质课评比一等奖。）