初中数学与信息技术融合案例

一、教材分析

《矩形的性质》是初中平面几何的重点教学内容之一。本课为华师大版初中数学八年级下册第19章第一节的内容，包括“矩形的性质”和“矩形的判定”两课，以及一篇阅读材料“完美矩形”。本课时的核心内容是探究矩形的基本概念及其性质，能掌握矩形和平行四边形的区别和联系，利用矩形的概念判定矩形，并应用矩形的性质解决实际应用问题。本课是承上启下的一课，此前学生已掌握了平行四边形的相关概念特征及判定方式，而矩形作为一类特殊的平行四边形，是针对前一章节知识点的延伸与拓展，是从“一般走向特殊”的典型数学学习形式，也为后续学习菱形与正方形这两个特殊的平行四边形奠定了基础。另外本节课的内容还渗透着转化、类比的数学思想，重在训练学生的逻辑思维能力和分析、总结、说理的能力。因此，这节课无论在知识上，还是在对学生能力培养上都有着非常重要的作用。

二、学情分析

1.授课对象：初中二年级学生。

2.认知基础：学生已掌握了三角形全等的证明、平行四边形的概念、性质、识别方法等基本知识，具备了基本推理能力。同时八年级学生的思维还依赖于具体、形象、易模仿的特点，因此学生的逻辑思维能力需要进一步加强。

3.认知障碍：对于性质的推理与证明及推论应用，学生可能会产生一定的困难，所以教学中要想方设法突破。

三、教学目标

1．掌握矩形的概念和性质，理解矩形与平行四边形的区别与联系

2．学会初步运用矩形的概念和性质来解决有关问题，渗透运动联系、从量变到质变的观点．

四、教学重难点和关键

1.重点：探索矩形的概念及其性质定理。

2.难点：灵活运用矩形的性质定理解决有关矩形的实际问题。

3.突破难点的关键：借助转化思想，用学过的知识解决未知问题。

五、教学方法和手段

1. 教学方法：任务型教学，在课堂中设计各项任务，让学生思考、推理、探究，使学生在动脑思考或动手实践的过程中发现问题、分析问题并解决问题，进一步培养学生的问题解决能力、创新能力及质疑精神。

2.教学手段：问题驱动，动手实验，分析思考，板书、多媒体相结合

六、教学过程

一、入 情景导入  生成问题

播放视频，请学生观看。

通过观看神舟16号的成功发射和凯旋归来的短视频，激发学生民族自豪感及爱国情怀，通过太阳帆板引出生活中的矩形。

矩形出现在我们生活中的方方面面，请几位同学分享一下身边的矩形。

矩形在生产生活中有着较为广泛的应用，本节课我们将对矩形的性质进行进一步的探究和学习。

【学生活动】观看视频，列举生活中的矩形

二、形 变换图形  形成概念

问题引入 问题引入——实验小剧场 实验小剧场

把平行四边形的一个角特殊化成直角，我们得到一个什么样的图形呢？这个图形我们小学学过吗？你能从这个图形与平行四边形的关系方面给出它的定义吗？

【师生活动】 】教师利用木条教具将平行四边形的一条边绕一个端点旋转，当一个角变为直角时，让学生观察所形成的图形，学生从这个图形与平行四边形的关系方面给出它的定义。

【自主探究】

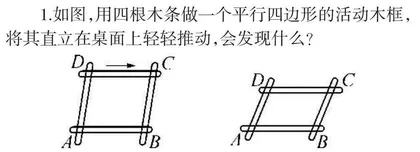
1．如图，用四根木条做一个平行四边形的活动木框，将其直立在桌面上轻轻推动，会发现什么？

（1）转动过程中的变化：角的大小变了，但不管如何，它仍然是一个平行四边形.

（2）保持平行四边形的原因：两组对边分别相等的四边形是平行四边形．

2．当移动到一个角是直角时停止，这时是什么图形？

矩形定义：有一个角是直角的平行四边形叫做矩形

学生自主实验，观察过程得出结论，运用所学知识进行推理。

【设计意图】让学生直观认识当一个角变化成直角时，平行四边形变成了矩形，利用问题串引导学生给矩形下定义。让学生从感性认识提升到理性认识。借助木条教具的动态演示，让学生直观感知角的变化带来平行四边形的改变，体会矩形与平行四边形间的关系，自然引出概念矩形是特殊的平行四边形，它具有平行四边形的所有性质．

【学以致用】

用一个简单练习检查学生学习效果。

三、 探究性质 深化认知

知识模块二 矩形的性质

问题 类似于平行四边形的性质推导，矩形ABCD的边、角、对角线方面是否有不同于一般平行四边形的特殊性质？

【自主探究】 活动一 动手折一折

1．矩形既是__中心对称图形__，也是__轴对称图形__，对称轴为：通过对边中点的直线__；

2.请用刻度尺、量角器等工具度量矩形四条边的长度、四个角的度数和对角线的长度及矩形邻边夹角度数，并记录测量结果。

追问1 1 ： 你得出了什么猜想？ ？

猜想1：矩形的四个角都是直角；

猜想2：矩形的对角线相等．

手动测量存在误差，如何验证这个结论的正确性？

追问2 2 ：你能否证明这些猜想？

猜想1的证明学生结合定义完成．

猜想2的证明方法较多，利用勾股定理、三角形全等、构造等腰三角形利用等腰三角形的三线合一都可进行证明。

鼓励学生尝试不同的证明方法。

【再探新知】

给出生活中的套圈游戏为背景，提问学生这个游戏是否公平？

【动手剪一剪 】究 自主探究  得出结论

推论：直角三角形斜边上的中线等于斜边的一半。

四、 运用性质 解决问题

例1 1 如图，矩形ABCD被两条对角线分成四个小三角形， 如果四个小三角形周长的和是86 cm， 矩形的对角线长是13 cm，那么该矩形的周长是多少？

知识延伸：

相邻两个小三角形的周长之差等于矩形邻边之差

引导学生分析矩形ABCD的对角线的性质，以及给其中的三角形带来的变化．

学生完成练习，自检今日学习情况

运用矩形的性质解决问题，进一步体会矩形中的角、线段、三角形之间的关系

四、结 归纳小结  反思提高

五、 布置作业，查漏补缺

必做题P100 练习1-3

阅读及预习作业：矩形的判定