浅谈数学教学中问题情境的创设及其作用

传统的教学，教师重视基础知识的教学和训练，但大量的解题训练使不少学生逐渐的厌烦数学，失去学习兴趣，成绩下降。《普通高中数学课程标准》提出：“倡导积极主动，勇于探索的学习方式”，“教师要创设适当的问题情景，鼓励学生发现数学的规律和问题解决的途径，使他们经历知识的形成过程”等，触动了我们对数学课堂情境教学的关注。我认识到：要持久、稳定的保持学生的优异成绩，需创设形式多样，丰富多采的教学情境，培养学生学习数学的兴趣，方能大面积提高教学质量。下面就在课堂教学中问题情境的创设谈自己的一得之见。

一、导入时创设问题情境——设疑，激发学生思维

导入时，教师有意识地创设问题情境——设疑，激发学生学习新知识的最佳心理状态。

1、联想生疑

在讲授新知识前，教师要提问本节课用到的旧知识，为学生积极思维创造条件，同时又能降低思维难度。例如在教学异面直线所成的角时，复习异面直线的概念后，继续问：“平面几何里，对于两条相交直线，我们用什么量来表示他们的关系呢？而对于两条异面直线他们的位置关系与什么量有关？”这样以旧引新设疑，引发学生的联想思维，为两异面直线所成角的概念及求法奠定了基础，使学生紧紧围绕两相交直线进行思考，难点得到突破。

2、动中生疑

让学生在动手操作中产生疑问，是激发学生学习动机的好方法。例“二面角”这节课，我作了如下设计：回顾两个平面的位置关系，要求学生把一张纸对折成两个半平面。

师：这两个平面是什么关系？

生：相交。

师：它们的交线——

生：折线。

师：转动其中一片纸，得到不同位置的相交平面，用什么区别它们的相交程度？

生：角度。

师：对，这是一个与我们以往所学的角不同的新的角，它有两个平面组成，我们来给它取个名字。

学生七嘴八舌，取出不少名字，经过分析归纳，最后给它命名为“二面角”（引出二面角的定义）

师：那么如何刻画这个角的大小呢？（学生比画手中折纸。）

生：用量角器量角的边缘。

师：二面角有边缘吗？（学生笑）

接下来有的学生用三角板贴“二面角”，有的学生垂直于棱折“二面角”``````议论纷纷，最后在大家的不同主张下引出二面角的平面角的定义，加深了对概念的理解，也出现了知识的正迁移，居然还发现了求二面角的另一方法：垂面法。

3、趣中生疑

教师在设疑时，不但要把“疑”设在重点处，而且要通过设疑，激发学生的兴趣。如：学习“用二分法求方程的近似解”时，先让同学们做一个猜字游戏，游戏规则是这样的：给定１～１００个自然数，通过操作键盘去猜这个数。对于每次猜测的结果，计算机的提示是“对了”或“大了”或“小了”。学生们纷纷举手示意来做这个游戏。师生共同完成一次猜数游戏后，问“你能在十次内猜出这个数吗？”一下子就把学生的注意力吸引住了，一声声“大了”“小了”，加上多媒体画面，学生很兴奋，课堂气氛活跃。教师又适时抛出一个问题，“你最少在几次内一定能猜出这个数？”，立即引起学生的积极讨论，在学生充满成功的欢快气氛中导入新课。

二、新授时创设问题情境——激疑，引导思维

设疑可揭示矛盾，启发学生的思维。激疑则是认识矛盾，从不知到知，从已知到新知的思维过程。

1、直观演示，激化矛盾

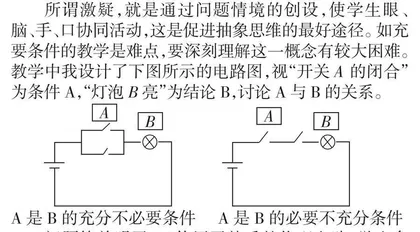
所谓激疑，就是通过问题情境的创设，使学生眼、脑、手、口协同活动，这是促进抽象思维的最好途径。如充要条件的教学是难点，要深刻理解这一概念有较大困难。教学中我设计了下图所示的电路图，视“开关Ａ的闭合”为条件Ａ，“灯泡Ｂ亮”为结论Ｂ，讨论Ａ与Ｂ的关系。

A是B的充分不必要条件               A是B的必要不充分条件

问题简单明了，又使用了熟悉的物理电路，学生参与的欲望强烈，从而对充要条件的概念理解得入木三分，从问题的解决中领悟了数学实质。

２、抽象概括，悟出道理

激疑的过程，也就是抽象概括的过程。如在“均值不等式”一节的教学中，设置如下问题情境：有两个商场在节前进行商品降价酬宾销售活动，分别采用两种降价方案：甲商场是第一次打p折销售，第二次打q折销售；乙商场是两次都打（ｐ＋ｑ）／２折销售。问哪个商场的价格最优惠？给学生创设了一个观察、联想、抽象、概括、数学化的过程，取得良好的教学效果。

3、观察比较，深化认识

激疑还应引导学生认识已有知识和新知识的内在联系，形成良好的知识体系。如学习圆锥曲线时，可创设问题情境，引导学生从定义、图形、标准方程、性质等方面进行比较，找出它们的联系和区别。通过多层次、多角度、多方面地对知识进行比较，既可以防止相似知识的混淆，又可以沟通联系，理清脉络，利于知识的理解和记忆。

三、读书时创设问题情境——质疑，促进思维

我们在新课讲完后，通过阅读课本使学生条理思维，整理知识，并对不理解或不懂的地方提出质疑。

1、教师质疑

创设问题情境，教师向学生质疑，目的是促进和引导学生质疑。如在学生掌握了：“用二分法求方程的近似解”的步骤后，教师不妨问学生：使用二分法有无条件？如果学生不能马上回答，可展示如下练习：下列函数图像中，不宜用二分法求函数零点的是（  ）

这样，就可使学生更准确的理解用二分法求函数零点的算法与算理。

2、创设质疑的机会，鼓励学生质疑

为了培养学生的质疑能力，鼓励他们大胆提出问题，有时教师可有意识的遗留一些问题，让学生在读书时发现。如在学习“等比数列求和公式”时，有意识的遗忘对公比为１的情况的讨论，让学生质疑，加深对知识的记忆和理解。

四、练习时创设问题情境——释疑，培养能力

练习是数学课堂教学中必不可少的一环。练习中，学生免不了会出错或提出问题，教师应适时、巧妙地为学生排疑解难。在释疑过程中，教师一方面要引导学生展现自己的思维过程，找出问题所在，另一方面，教师要设置问题情境，也要充分暴露自己的思维过程，让学生在这些探索、发现及判断等真实的思维过程中，学会运用已有知识进行联想、分析、归纳、类比，切实掌握研究问题的基本思想、思考和解决问题的基本方法，从而提高思维能力。

总之，在教学过程的每一个环节，都可以适时创设问题情境，激发学生的思维，改变学生在学习中的消极被动状态，发挥学生的主体参与意识，充分调动学生学习的积极性，大面积提高教学质量，持久、稳定的保持学生的优异成绩。