初中数学试题命制的五个转向
作者: 杨艳 邓昌滨随着2022年版义务教育课程方案和各学科课程标准的颁布,新一轮课改也在向“深水区"迈进。落实新课改理念,试题命制是关键,因为它实际上在更大的程度上指挥着教学实践。但是,基于《义务教育数学课程标准(2022年版)》(以下简称“新课标"中的考试命题建议,综观当下的初中数学试题命制,发现其仍然存在一些误区,需要完成一些转向。
一、考查内容:从以考定教走向依标设考
2019年,教育部明确提出:取消初中学业水平考试大纲或考试说明,切实做到学(教)什么考什么,而不是考什么学(教)什么。新课标将其中规定的课程目标、内容要求、学业要求和学业质量作为试题命制的依据,便要求考查内容从以考定教走向依标设考。
【案例1】2024年某市中考数学模拟卷第14题的命制改进
原题:已知二次函数 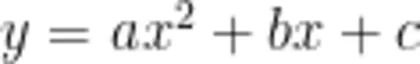 的图像经过点 A ( - 1 , - 4 ) 、 B ( 3 , 0 ) 和 C ( 1 , 2 ) .求这个二次函数的表达式。
的图像经过点 A ( - 1 , - 4 ) 、 B ( 3 , 0 ) 和 C ( 1 , 2 ) .求这个二次函数的表达式。
本题主要考查利用待定系数法求二次函数表达式。可以把 A , B , C 三点的坐标分别代入函数表达式,得到 a - b + c = - 4 , 9 a + 3 b + c=0 , a + b + c=2 ,即关于 a, b, c 的三元一次方程组,由此解得 a, b, c 。但是,新课标把“解简单的三元一次方程组”设定为选学内容,不作为考试要求。因此,本题的考查内容超出了课标要求。
改进:已知二次函数 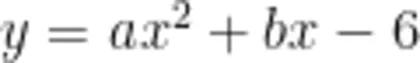 的图像经过点 A ( - 1 , - 4 ) 、 B ( 3 , 0 ) 和 C ( 0 , 2 ) 中的两个,求这个二次函数的表达式。
的图像经过点 A ( - 1 , - 4 ) 、 B ( 3 , 0 ) 和 C ( 0 , 2 ) 中的两个,求这个二次函数的表达式。
改进后的试题仍然考查利用待定系数法求二次函数表达式。由题意,易得抛物线与 y 轴交于点 ( 0 , - 6 ) ,所以抛物线不可能过点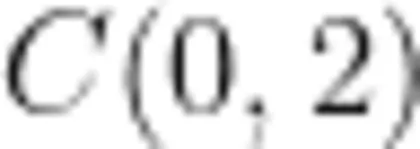 ,只能过点 A ( - 1 , - 4 ) 和 B ( 3 , 0 ) 。由此,可以列出二元一次方程组,解得 a = 1 .b = - 1 。因此,改进后试题的考查内容没超出课标要求。同时,改进后的试题还进一步考查了函数的概念(表达式和图像)和逻辑推理能力。
,只能过点 A ( - 1 , - 4 ) 和 B ( 3 , 0 ) 。由此,可以列出二元一次方程组,解得 a = 1 .b = - 1 。因此,改进后试题的考查内容没超出课标要求。同时,改进后的试题还进一步考查了函数的概念(表达式和图像)和逻辑推理能力。
二、命题立意:从知识立意走向素养立意
新课标将核心素养确立为课程教学的终极目标。试题命制不能单纯地考查学生的知识和技能,而要在知识、技能的融通与应用中着力考查学生的素养,尤其要强化对思维(探究)过程的考查,突出开放性、创新性等,从而从知识立意走向素养立意。
【案例22024年某市中考数学模拟卷第5题的命制改进
原题:下列几何体中,是圆柱的是(
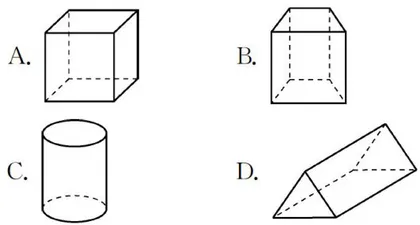
本题主要考查圆柱的特征,属于单纯的知识立意:学生只要知道圆柱是由两个圆形的底面和一个弯曲的侧面围成的,就能顺利求解。
改进:下列几何体中,与其他几个不同类的是 1
选项同原题(这里省略)。
改进后的试题不再孤立地考查圆柱的特征,而既综合地考查棱柱和圆柱的特征等相关知识,又深入地考查推理能力等核心素养:学生不仅要了解圆柱的特征,而且要了解其他几何体的特征,同时要对比分析不同的几何体,寻找其异同,归纳其类型。
三、价值导向:从考试立场走向育人本位
试题不仅有评价的功能,也应是育人的 载体。因此,数学试题命制不能只站在考试 立场,还应紧密围绕“立德树人"根本任务,传 递数学文化,润泽学生情感,彰显育人价值。
【案例32024年某市中考数学模拟卷第9题的命制改进
原题:比较大小: 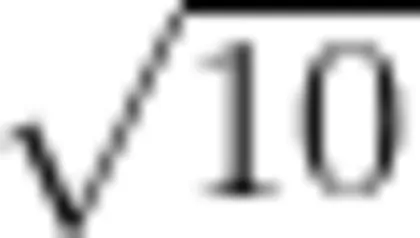
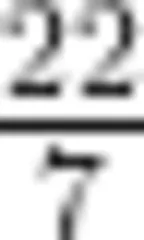 (填“>”专 < ”或“
(填“>”专 < ”或“ 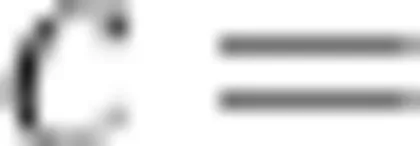 ”)。
”)。
本题主要考查实数的大小关系,熟练掌握其比较方法是解题的关键。考虑到考试还承载着育人功能,可以在本题中适当融入中华优秀传统文化的内容。
改进:我国古代科学家张衡将圆周率取近似值为 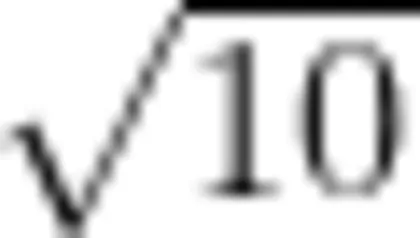 ,数学家祖冲之给出圆周率的一种分数形式的近似值为 。比较大小:
,数学家祖冲之给出圆周率的一种分数形式的近似值为 。比较大小: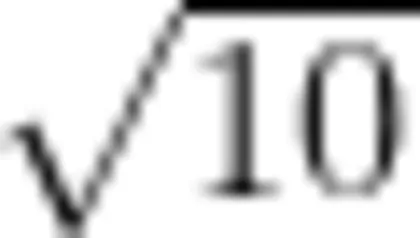 (204
(204 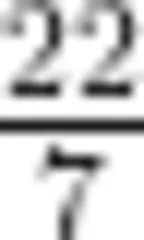 (填“ > ""<”或“
(填“ > ""<”或“  ”)。
”)。
本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:jyzy20250208.pd原版全文
改进后的试题融人我国古代科学家张衡与数学家祖冲之研究圆周率的成就与贡献,使学生在解题过程中油然而生出对我国学者的敬佩之心,从而增强了学习数学的动力,坚定了学好数学的信心。
四、问题情境:从直接运用走向迁移运用
新课标指出:试题命制要根据考查意图,结合学生认知水平和生活经验,设计合理的数学情境、生活情境、科学情境,关注情境的真实性,并适当引入数学文化。从问题情境上看,试题命制要从简单地创设直接运用知识、技能和素养、思维的问题情境走向有铺垫地创设迁移运用知识、技能和素养、思维的问题情境,引导学生看见知识联系,发现方法本质,自然地进行迁移运用。
【案例42024年秋学期某市七年级期中数学试卷第12题的命制改进
原题:计算 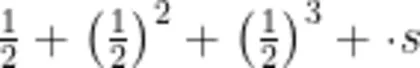
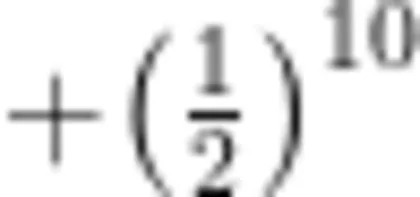
本题简约但不简单:学生如果不能深度思考以灵活运用等比数列的变化规律,只能一味地死算,则会陷入烦琐的计算——显然有悖于命题者的意图。当然,此题灵活运用等比数列的变化规律求解(设原式  ,两边同乘后,两式相减,可求得x=1-1) 210),对于刚刚进入初中半个学期的学生来说,难度也比较大;而且需要解一元一次方程,有超标的嫌疑。
,两边同乘后,两式相减,可求得x=1-1) 210),对于刚刚进入初中半个学期的学生来说,难度也比较大;而且需要解一元一次方程,有超标的嫌疑。
改进:《庄子·天下》中说:“一尺之棰,日取其半,万世不竭。”意思是:一尺长的木棍,每天截取一半,永远也截不完。我国古人在两千多年前就领悟了数学中的极限思想。今天我们运用这一数学思想研究下列问题。
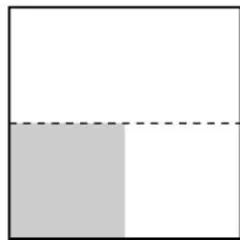
(1)如图1,将边长为1的正方形剪掉一半,则 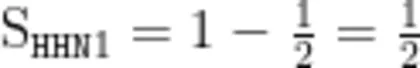 2;如图2,在图1的基础上,将阴影部分再剪掉一半,则
2;如图2,在图1的基础上,将阴影部分再剪掉一半,则 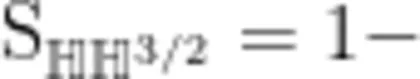
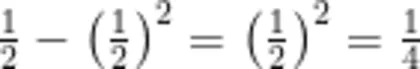 ;以此类推,如图3,
;以此类推,如图3,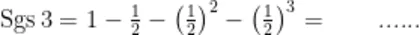
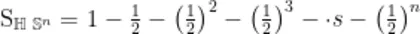
(2)计算 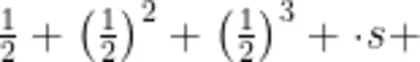
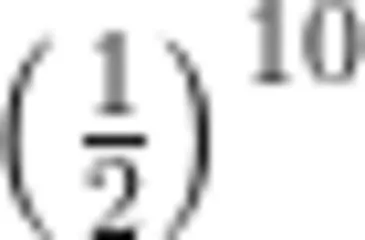 。
。
改进后的试题扩展了原来的简单情境,以中国古代数学文化为背景,紧密联系日常生活,给予启发和引导,让学生建立知识联系,发现方法本质,进而迁移运用解决问题。这个过程十分自然,让学生感觉不像在做数学题,而像在真实的场景中运用所学的数学知识与方法帮助他人解决了一个问题。
五、测量学指标:从难度越位走向适度区分
根据测量学理论,一般是在考后,对试题的信度、效度、难度、区分度等指标进行定量评价,但是,在实际操作中,更需要在考前,对试题的难度、区分度等指标进行定性评价。其中,特别需要关注的是,试题的难度影响着试题的区分度,因此,在具体实践中,尤其要注意从难度越位走向适度区分。
【案例52024年秋学期某市九年级期中数学试卷第25题的命制改进
原题:(1)圆周角的度数等于它所对孤上的圆心角度数的 [
A.两倍 B.一半C.三倍 D.三分之一
(2)如图4,点 D 在以 A B 为直径的 ? O 上, D C ⊥ A O 于点 C ,且 A C=C O ;延长 A B 至E ,连接 D E ,交 ? O 于点 F ,使得 E F=O A ;弦D H 交 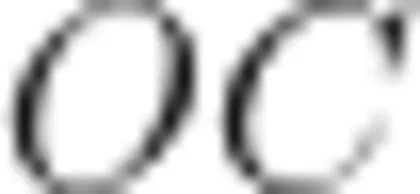 于点 G ,满足
于点 G ,满足 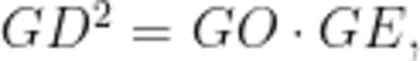 。若
。若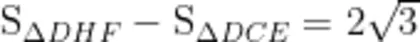 ,则 F H 的长为( )
,则 F H 的长为( )
A.6 B.8 C. 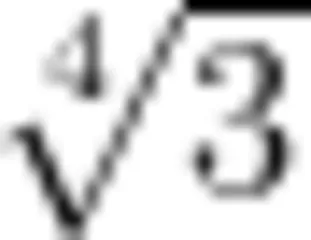 (20号 D. 12
(20号 D. 12
本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:jyzy20250208.pd原版全文