一道高中数学教材习题的跨学科学习元素挖掘

《普通高中数学课程标准（2017年版2020 年修订）》在“课程理念"中指出高中数学课程“强调数学与生活以及其他学科的联系"1]；在"学业质量"水平三（最高水平）中要求学生“能够合理地运用数学语言和思维进行跨学科的表达与交流"2]。实际上，在基础教育阶段，开展跨学科学习，促进“学科融合”，是一种世界潮流[3]，有助于学生综合能力、创新素养的发展[4]。然而，在实际的教学中，很多教师找不到恰当的跨学科学习内容（材料、问题、任务、项目等）。对此，我们认为，教师首先要用好教材，充分挖掘教材内容（尤其是关于数学建模活动与数学探究活动以及数学文化5的内容）中蕴含的跨学科学习元素。以下重点挖掘一道教材习题中蕴含的跨学科学习元素，以供参考。

一、教材习题及其解答

苏教版高中数学必修第一册第8章《函数应用》中的“应用与建模"板块在介绍了根据生物学常识和测量数据建立动物体重与脉搏关系的函数模型的基础上，给出了如下习题：

下页表1给出了八大行星与冥王星离太阳的距离和它们运行的周期，试建立这两组数据之间的关系。

对此，根据前面的介绍，学生可用Excel（或其他软件）作出数据的散点图，再用“添加趋势线"工具（或其他“数据拟合"功能），在“线性、对数、多项式、幂、指数、移动平均”这六种类型中选择 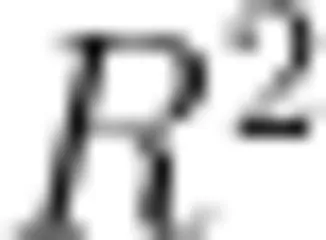值最大的一种，得到指数函数模型 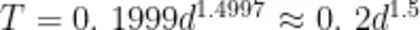（其中 T 表示周期， d 表示距离），如图1所示。

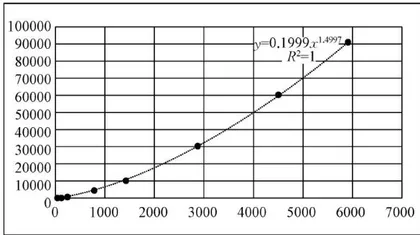
如果学生学习过线性回归方程（本题可以在高中数学复习教学中“再使用”），教师可以提出问题：如何不用Excel（或其他软件），直接求出拟合函数？对此，教师可以引导学生想到根据两个相关变量的两组对应数据求线性回归方程（线性拟合函数）的方法，以及对数“化乘除为加减、化指数为乘除”的功能，从而对已知数据取常用对数（结果如表2所示），然后代人公式计算得到线性回归方程y = 1 . 4 9 9 7 x - 0 . 6 9 9 1 ≈ 1 . 5 x - 0 . 6 9 9 1 （其中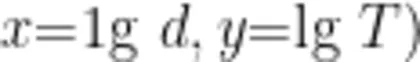 。由此，让学生认识到线性回归方程的巨大应用价值：非线性的关系也可以通过转化进行线性拟合。

二、习题中跨学科学习元素的挖掘

数据拟合是一种重要的统计方法，在自然科学和社会科学的各个分支中都有十分广泛的应用。上述习题中的数据拟合具有物理学（天文学）应用背景，我们可以进一步挖掘其中的跨学科学习元素。

（一）分析拟合函数中系数的单位，挖掘出量纲分析方法

一般地，可以将上述拟合函数记为 T = 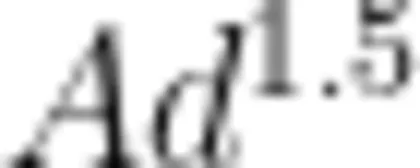。从实际意义的角度看，这里的变量 T 、d 都是有单位的，其国际标准单位分别为s、m ，因此，常数系数 A 也是有单位的，其国际标准单位为 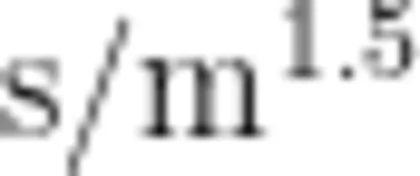。教学中，可以引导学生思考：（27秒） z= （ 9 米）有实际意义吗？如何解决这个问题？从而得到常数系数 A 的单位。

这里便涉及量纲分析方法。在国际单位制下，任意一个物理量 Q 都可以唯一地表示为七个基本物理量（质量、长度、时间）的幂的积，记为 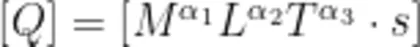，称为 Q 的量纲式（量纲）。只有量纲相同的量（表达式）才能进行加减运算或利用等号（不等号）连接。因此，量纲分析是一种快捷而有效地检验物理（包括几何）公式的方法。例如，如果上述拟合函数中常数系数 A 的国际标准单位不是 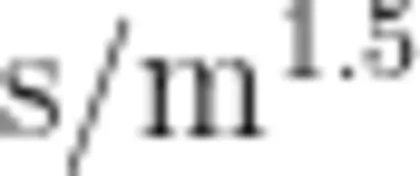，那么该函数式不可能成立。再如，某人解题时得到 F = m ν ，因为左边的量纲是 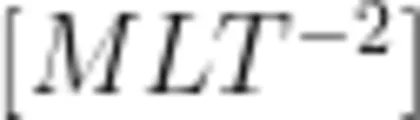，右边的量纲是 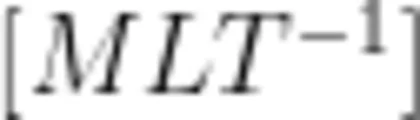，二者显然不同，所以该结果一定错误。

这里要注意：即使量纲相同，也不能保证两个量（表达式）相等，因为数字系数是无量纲的，它们可能还相差一个数字系数。因此，熟悉一些无量纲数（如三角函数、离心率、面积比、体积比、概率），对灵活运用量纲分析方法很有好处。

量纲分析方法在数学、物理跨学科学习中非常有用，应当得到重视。

例如2022年4月湖北省武汉市高中数学调研卷第8题：

某同学在课外阅读时了解到概率统计中的切比雪夫不等式，该不等式可以在随机变量 X 的数学期望 E （ X ） 与方差 D （ X ） 存在但分布位置未知的情况下，对事件“ X - 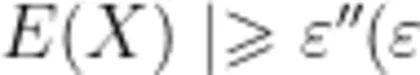为任意正实数）的概率作出上限估计。切比雪夫不等式的形式为 P （ ∣ X - E （ X ） ∣  ε ）f （ D （ X ） ， ε ） ，其中 f （ D （ X ） ， ε ） 是关于 D （ X ） 和 ε 的表达式。由于记忆模糊，该同学只能确定 f （ D （ X ） ， ε ） 的具体形式是下列四个选项中的一个。请你根据学过的知识，确定该形式是 ）

A. 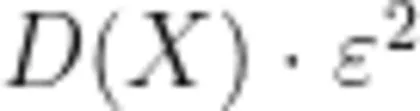（204号 B. 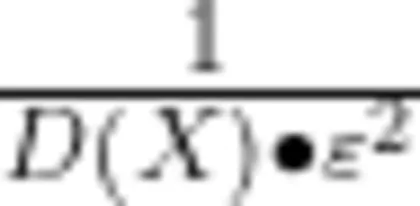C 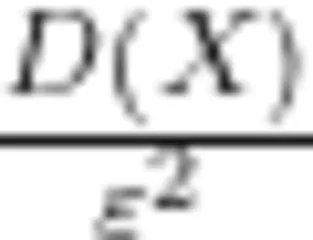D. 2 D（X）

显然，本题不是考查高中生对大学概率统计中切比雪夫不等式的了解，而是要求他们灵活利用所学知识（不一定是数学知识）解决问题。注意到切比雪夫不等式左边是一个概率，因此，可认定其右边也是一个无量纲数。一旦我们对随机变量 X 赋予一定的量纲（如熟悉的长度单位“米"），则 E （ X ） ，ε也具有同样的量纲， D （ X ） 的量纲为 X 量纲的平方。由此，可排除选项 A， B 。下面，进一步考虑 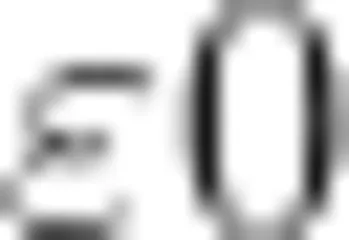的情况。此时， P （ ∣ X-E （ X ） ∣ ≥e）→1，而D（x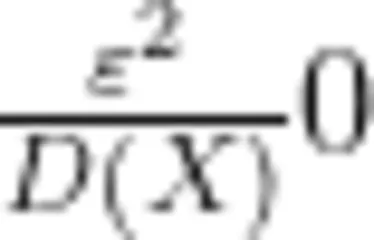） 。由此，可排除选项 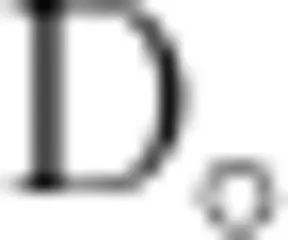因此，正确选项只能是C（实际上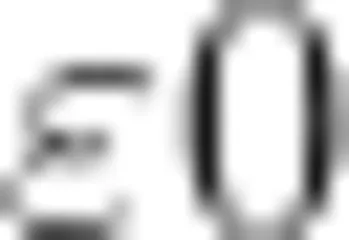， 时，D（X）→+o，，不等式显然成立）。

再如一道复旦大学自主招生数学试题：

本题如果从正面直接求解，则会有不小的计算量。我们可以先从量纲的角度分析：显然，所求和式的量纲应该为长度的一2次方，由此，可以排除选项 C， D 。再考虑 a b 的极限状态：此时，椭圆退化为圆，显然，所求和式大于0，由此，可以排除选项 B 。因此，正确选项只能是A。

（二）分析拟合函数中系数的意义，挖掘出物理学规律进一步研究可以发现，常数系数A=不随变量 T ， d 的变化而变化，它有更明确的物理意义。为此，需要进一步思考数据拟合结论蕴含的物理规律。

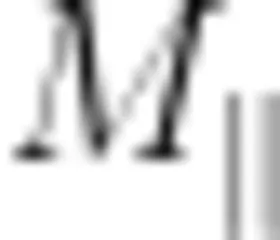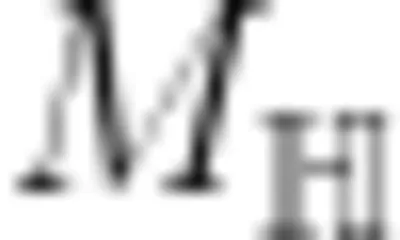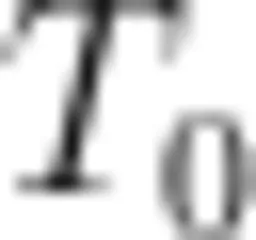既然常数系数 A 仅与中心天体太阳的质量有关，便可试着迁移到中心天体为地球的情境，类比求出地球的同步卫星距离地面有多高。显然，只要将前面得到的关系中的 换成 . 换成 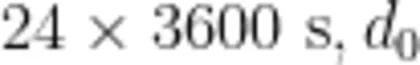换成 6 . 4 × 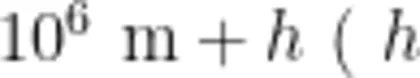为地球的同步卫星到地面的距离），即可算得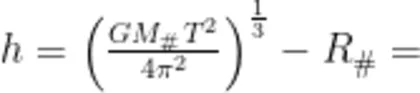

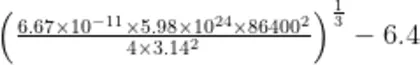
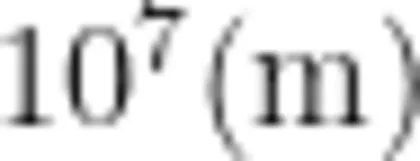。其与我们熟知的理论值 k m 也吻合得很好。

当然，如果进一步拓展思考，还可以发现这个结果正是高中生熟知的开普勒第三定律（这里不再具体阐述了）。

最后需要指出的是，苏教版高中数学教材的每一章都设计了“问题与探究”“应用与建模”“阅读”等数学建模活动与数学探究活动或数学文化方面的板块（栏目），它们是挖掘跨学科学习元素的“富矿”再如《数列》一章的“阅读"板块介绍了斐波那契数列，也是挖掘跨学科学习元素的极好材料。

参考文献：

[1][2][5]中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）[S].北京：人民教育出版社，2020：2，78，9-10.

[3]史宁中.课程标准修订与核心素养[J].教育研究与评论，2022（5）：20.

[4]刘祖希.关于数学跨学科内容与教学的已有研究：兼及2022年全国高考数学试卷跨学科试题分析［J].教育研究与评论（中学教育教学），2022（12）：5.

[6]G.波利亚.怎样解题：数学教学法的新面貌M」.涂泓，冯承天，译.上海：上海科技教育出版社，2002：204－207.

[7]余晓娴.在跨学科融合中提升数学建模核心素养：基于量纲分析的数学建模教学微设计［J].高中数学教与学，2022（4）：9－11+ 1 3