基于随机森林算法的打叶工艺参数优化

摘要 通过建立随机森林回归模型，筛选出在梗叶分离参数中影响片烟中片率的9个重要特征参数。通过模型优化和预测，模型回归评分为0.622，预测值与真实值之间的平均相对误差小于5%。模拟结果的相关性分析表明，在多因素影响、非线性关系且关系复杂的情况下，随机森林回归模型仍然可以较好地预测不同叶梗分离参数下的中片率。该方法可为打叶工艺参数的优化提供技术支持。

关键词 打叶复烤；中片率；参数优化；随机森林

中图分类号 TS 44+3  文献标识码 A

文章编号 0517-6611（2022）20-0162-04

doi：10.3969/j.issn.0517-6611.2022.20.042

Optimization of Threshing and Redrying Process Parameters Based on Random Forest Algorithm

LU Pei-lin，TIAN Qing，LI Rui-dong et al

（Yunnan Tobacco Redrying Co.，Ltd.，Kunming，Yunnan 650000）

Abstract Through establishing random forest regression model，9 important  characteristic parameters that influenced the percentage of medium-sized strips in the stem-leaf separation parameters were screened out.Through model optimization and prediction，the model regression score was 0.622，and the average relative error between the predicted value and actual value was less than 5%.The correlation analysis of the simulation results showed that under the conditions of multi-factor influences，non-linear relationship and complex relationship，random forest regression model could predict the percentage of medium-sized strips under different leaf-stem separation parameters.

Key words Threshing and redrying;Percentage of medium-sized strips;Parameter optimization;Random forest

打叶复烤是卷烟工业企业进行原料初挑、模块配方、均匀性提升的重要环节［1］。近年来，随着各卷烟企业重点品牌对成品片烟核心质量指标均匀性水平要求的不断提高，打叶复烤企业在参数设置和优化管控方面进行了大量研究。杨凯等［2］通过烟碱值的组配模式，探索出基于烟碱变异系数的均质化控制模式。皮亮等［3］结合历史数据，以过程工艺和参数标准化为切入点， 有效控制过程质量稳定性， 从而使最终产品质量指标稳定性显著提升。杨洋等［4］通过多指标权重分析和正交试验对遵义复烤新线工艺参数进行优化。黄小艳等［5］通过Scikit_learn中的决策树算法和正交试验，根据加工历史数据，使用机器学习方式对打叶复烤的水分参数进行了优化。通过以上研究使产品的化学成分指标、叶片结构指标的均匀性有了明显提升，但在过程质量管控和数据价值的利用上仍有待加强。

2001年，Breiman［6］将决策树集成组合成随机森林。随机森林算法是一种非常具有代表性的机器学习Bagging集成算法［7］，它以决策树作为基评估器，多棵树随机组成的森林也叫随机森林，包括随机森林分类器和随机森林回归器（random forest regressor）。成浩科等［8］使用随机森林算法建立了河流总磷的预测模型，分析了河流总磷的影响因素。苏志同等［9］也使用随机森林算法对铝电解煅烧工艺参数进行了研究。由于决策树算法本身存在的局限性，决策树模型预测效果比随机森林模型容易过拟合且受异常值的影响更大。张莉等［10］使用随机森林和逻辑回归分类模型，对各类烟叶样品的外观质量指标和感官质量指标进行关联分析，使精选效率大幅度提升，选出的烟叶工业适用性也明显提高。 为适应卷烟工业企业对片烟中片率的要求，进一步分析中片率与打叶复烤工艺参数之间的相关性，笔者采用随机森林回归器对2021年叶梗分离工艺参数和片烟中片率进行回归建模，以期找到打叶复烤打叶工艺参数优化调控的方向。

1 研究数据与方法

1.1 研究数据

选取2021年泸西复烤厂配方烟叶产地相近、产品质量指标要求相同的出口备货烟叶模块共计43个，从17 646个数据中筛选出涉及叶梗分离段一打、二打、三打、四打、五打和一至十二风分共计33项工艺参数及中片率数据，共9 792个数据。相关数据来自泸西复烤厂2021年中控系统的操作日志。将选取的数据集记为D={xij}（i=1，2，…，n;j=1，2，…，m），其中n和m分别表示样本数和指标数。

1.2 随机森林回归算法

随机森林是一种集成学习算法，集成多个决策树算法对相同现象产生重复的预测结果，利用bootstrap 重抽样方法从原始样本中抽取多个样本，对每个bootstrap 样本构建决策树，然后将所有决策树预测平均值作为最终预测结果。随机森林回归可以看成是由多个弱预测器（决策树）集成的强预测器，抵消了部分随机误差，对异常值和噪声具有很好的容忍度。

随机森林回归算法步骤可归纳如下：

设从独立分布的随机向量（X，Y）中抽取训练集，输入向量为X，输出向量为Y，则预测输出h（X）的均方泛化误差为EX，Y［Y-h（X）］2。

设θ为随机参数向量，则对应的决策树为T（θ）。

（1）数据集的随机选取。利用bootstrap方法从原始数据集D中有放回地随机抽取K个样本子集，记作θi（i=1，2，…，k），并由此生成k棵回归树{T（x，θi）}（i=1，2，…，k），每次boot-strap抽样未抽到的样本组成了k个袋外数据（out-of-bag，OOB），未被抽中的概率为（1-1n）n，其中 n 为原始数据 D的样本量。当样本量 n 较大时，（1-1n）n将收敛于1e，约为0.368，表明原始样本集中约有 36.8%的“袋外数据”可能不在子样本集中，将其作为随机森林的测试样本。

（2）特征的随机选取。在每棵回归树的每个节点处从m个特征中随机抽取mtrain个特征（mtrain<m），作为当前节点的分裂特征集，并以这mtrain个特征中最好的分裂方式对该节点进行分裂。

（3）随机森林的生成。每棵回归树开始自顶向下的递归分枝，直到满足分割终止条件。

（4）OOB估计及模型评价。将生成的k棵回归树组成随机森林回归模型，回归的效果评价采用袋外数据（OOB）预测的残差均方（MSE）和拟合系数（R2）。计算公式如下：

MSE=1nni=1（yi-iOOB）2

R2=1-ni=1（yi-iOOB）2

ni=1（yi-）2

式中，yi为袋外数据中因变量的真实值，iOOB为随机森林对袋外数据的预测值，表示样本平均值。

（5）模型优化。通过多次循环生成随机森林回归模型，求出每次循环的模型拟合系数和均方根误差值，得到最优决策树大小参数、决策树最大深度参数、内部节点再划分所需的最小样本参数、叶子节点最小样本数、最大特征数。

（6）特征重要性评价。特征重要性评价通常使用基尼指数（Gini index）或者袋外数据（OOB）错误率作为评估指标来衡量，采用袋外数据（OOB）错误率作为评估指标。对于随机森林回归中的变量重要性评分（variable importance measure，VIM），使用基于permutation随机置换的残差均方减小量进行衡量。具体过程如下：

a.每一个自助样本建立一个回归树模型，同时使用该模型对相应的袋外数据OOB进行预测，得到k个袋外数据的残差均方，记为MSE1，MSE2，…，MSEk。

b.变量Xi在k个OOB样本中随机置换，形成新的OOB测试样本，然后用已建立的随机森林对新的OOB进行预测，与第一步的计算方法相同，得到随机置换后的OOB残差均方，得到以下矩阵：

MSE11…MSE1k

MSEq1…MSEqk

c.用MSE1，MSE2，…，MSEk与OOB残差均方矩阵对应的第i行向量相减，平均后再除以标准误差得到变量Xi的重要性评分，即

scorei=1SE［kj=11k（MSEj-MSEij）］

2 结果与分析

2.1 随机森林规模参数及其他参数的优化

模型规模参数（n_estimators）代表随机森林中树木的数量，即基评估器的数量。这个参数对随机森林模型精确度的影响是单向的，模型规模参数越大，模型的效果往往越好。同时，任何模型都具有决策边界，当模型规模参数达到一定数值后，随机森林的精确度往往不再上升。为了获取最优的模型效果，使用300次循环，计算不断调试模型规模参数（得到学习曲线），求出每次循环的模型拟合系数和均方根误差，并以可视化形式进行展现，便于求得最优参数值。

经过循环计算得出的最优拟合系数和均方根误差见表1。当模型规模参数为93时，以最优拟合系数作为衡量标准时，随机森林模型精确度最大；当模型规模参数为17时，均方根误差最小。

通过观察学习曲线（图1）发现，当模型规模参数为93时，曲线均处于平稳状态，此时均方根误差为7.21，均方根误差稍有增加。为了保障模型精确且稳定可靠，选择93作为随机森林规模参数（Scikit_learn中均方根误差被认定为一种误差，因此显示为负值，真实的均方根误差为其显示的绝对值）。

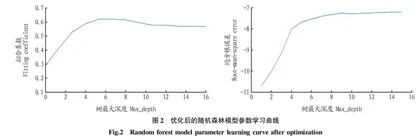
随机森林模型在模型规模参数为93时，采用循环算法绘制出的树最大深度（Max_depth）学习曲线见图2。表2为优化后模型拟合系数与均方根误差的变化。由于拟合系数和均方根误差的最优值不同，根据参数变化百分比选择对损失百分比最小的参数模型，并建立随机森林回归模型。

2.2 随机森林模型模拟结果 随机森林对中片率的模拟结果见图3。图3显示出坐标点距离直线越近，表明预测值与实际值越接近。对预测值和实际值进行相关性分析，相关系数为0.782，预测值与实际值存在较强的非线性相关性。在多因素影响、非线性关系且关系复杂的情况下，随机森林仍然可以较好地预测不同叶梗分离参数下的中片率。

2.3 模型的重要特征因素评价

在兼顾模型精确性和稳定性，实现综合性能最好时，将剩余的70%测试集数据导入模型，选取决策影响度大于5%的因素作为重要特征参数，得出影响模型决策的参数特征重要度排序，见表3。从表3可以看出，针对此次建模所采用的参数指标，二打一联打辊转速、五打打辊转速、三打打辊转速和一打打辊转速是叶梗分离参数中影响最大的4个工艺参数指标，其中二打一联打辊转速和五打打辊转速对中片率的影响最大，分别占比18.01%和18.31%。

2.4 基于重要特征因素和回归关系的试验验证

利用Values语法读取出测试集数据，选取测试集中的9个重要特征因素进行预测，结果如表4所示。然后，再将中片率的预测值与真实值进行对比，结果见图4。