小学数学解决问题策略模块化的实施路径
作者: 彭龙龙
摘 要 “解决问题策略模块化”是一种基于整体的、结构化的教学视野,以解决问题策略学习为统领,以四大知识领域为目标,将具有相同解题策略的问题通过整合、重组和开发来实施的课堂教学。在教学过程中可以连接数学思想、策略与方法,构建解决问题策略模块;加强策略在不同学习领域和年段之间的联系,灵活运用解决问题策略模块;建立结构,实现策略互通,内化解决问题策略模块。
关 键 词 小学教学 解决问题策略 模块化 解决问题能力 策略模块
引用格式 彭龙龙.小学数学解决问题策略模块化的实施路径[J].教学与管理,2022(29):54-56.
“解决问题”就是引导学生运用相关知识,采用数学策略寻求问题解决的过程[1]。它同概念教学、计算教学、图形与几何教学、统计与概率教学一样,是数学教学的重要组成一部分。现行的义务教育人教版教学教材并没有设置独立的解决问题策略单元,而是将解决问题策略分散融入各册各个单元版块中去,这在降低学习难度的同时,也使解决问题策略的渗透过于零散,缺乏系统化。
基于此,笔者在经过了长时间的深入思考和对其他版本教材的深度解读后提出“小学数学解决问题策略模块化”实践研究。解决问题策略模块化其实是一种基于整体的、结构化的教学视野,以解决问题策略学习为统领,以四大知识领域为目标,将具有相同解题策略的问题通过整合、重组和开发来实施的课堂教学。这是一种以解决问题为背景的学习模式,它最大的价值在于让策略不再是独立存在的,而是相互关联、融通的策略模块,最大化地实现学生解决问题方法体系的整体架构。同时,深层挖掘“解决问题的策略”所蕴含的数学思想方法,并在策略模块的动态生成过程中,以教师有结构的教促进学生有关联的学,最终指向学生解决问题能力的有效提升[2]。
一、深度勾联,建构解决问题策略模块
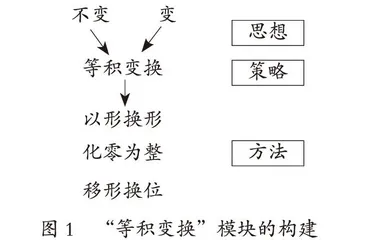
解决问题的数学思想、解决问题的策略、解决问题的方法是学生数学思维水平的三个层次。数学思想是现实世界的空间形式和数量关系在人的意识中,经过思维活动而产生的结果。策略是学生为解决问题而展开数学思维时的尝试、选择和优化的过程。策略是方法的灵魂,是对方法本质的认识,是运用方法的指导思想。策略是思想的雏形,是形成数学思想的有力支撑。小学生在解决问题过程中达成的是方法,渗透的是策略,孕育的是思想[3]。因此,对各种解决问题策略、思想、方法的关联性研究与探索将为小学数学解决问题策略模块化的建构奠定坚实的基础。如笔者研究团队的一节解决问题策略模块化研讨课“等积变换”。从数学的角度看,世界上的事物是千变万化的,而变化中又蕴含着不变的因素。其中,“变中有不变”是我们解决问题的重要突破口,也是重要的数学思想之一。而等积变换作为蕴含“变与不变”这一数学思想的重要载体,它的价值十分明显。正是基于这样的思考,我们在课堂实践之前就勾勒出了以思想、策略、方法三个维度搭建的顶层设计蓝图(如图1)。
上课伊始教师出示两道典型例题“平行四边形停车场设计”和“测量西红柿的体积”,随后追问:“这两道题有什么共同特征?什么变了,什么不变?”从而快速唤醒学生头脑中关于“变与不变”的数学思想,随后揭示图形与几何领域中研究“变与不变”这一类问题的方法,紧接着带领学生回忆小学阶段“等积变换”的深度应用,让学生在回忆中看到更多关于图形的形状、位置、角度变了,但面积或体积不变的问题(见表1)。
等积变换作为一种策略本身具有一定的宏观性,即使学生认识到这类问题的大量存在,也缺少适合的解决方法。为此,我们在教学过程中适时引入化零为整、以形换形、借形补形、移形换位等具有操作性的方法。这样的设计顺承有序、结构清晰,在策略模块的建构中将数学思想、策略与方法三者深度勾联,形成一个结构化的课堂架构。
二、优化提升,运用解决问题策略模块
学生对策略进行横向(领域)与纵向(年级)迁移,其实就是从问题解决的角度让学生明白不同问题之间具有内在的联系,可以用所生成的策略模块解决问题。学生在运用的过程中,会呈现出不同的解决思路与方法,但这些方法的产生是零散的、自发的。如果只满足于方法与策略的多样,学生的思维并没有得到有效发展,为此要对学生的策略方法进行优化提升。如笔者研究团队的一节研讨课“解决问题策略——尝试法”。尝试法是学生在解决问题过程中,通过仔细观察,不断试误、调整,逐渐减少无关的错误内容,最终找到正确答案,解决问题。
而正是这样一节课,教师在初次磨课后对学生进行访谈,听到更多是“太麻烦了,没有别的方法可用”的声音。究其原因,学生不认同尝试是一种方法,甚至瞧不起这种“笨”办法,无法真正体验到尝试策略的独特价值。为此,教师认为需要对尝试策略进行优化提升,充分显现其作为解题策略的“好”,以寻求与学生认知需求的共鸣,激发学生的策略使用意识。因此在利用典型题唤醒学生头脑中的“尝试”策略后,我们引入了图形与几何领域中的一道经典例题:爷爷用长24米的篱笆一面靠墙围了一块长方形的菜地,这块菜地的面积最大是多少平方米(长和宽均为整数米)?面对此题,学生采用了不同的方法。大部分学生选择了一一列举的方法,这与他们头脑中对尝试的最初印象是一致的,不就是一个一个去试吗。而一部分学生受之前的结论“周长相等,正方形面积最大” 的负迁移,认为这题的最大面积是“边长为8米的正方形的面积,即8×8=64(平方米)” 而这个隐匿在学生头脑中的“错误”,就是尝试策略的切入口。教师顺势引导学生观察:以8×8=64为中心,向右调整面积变小,不符合题意;向左调整面积变大,当长=12,宽=6,面积为72平方米时,是最大吗?无法判断,继续往左试,面积又变成了70平方米,变小了(如图2)。此时,最大面积找到了。这样的教学不仅是在与列举策略的对比中直指尝试策略的内核“试”与“调”,更是带领学生走进了思辨的场域,从低水平的思维走向高阶层的思维。同时也打破了学生对“尝试”的原有认知(一个一个去试),进一步完善了学生的认知结构。
三、建立结构,内化解决问题策略模块
教育的目的是实现自我教育, 而解决问题策略模块化的目的是从最初的深度建构、灵活运用,走向自觉内化[4],在策略模块间建立联结,实现策略互通。如笔者研究团队的一节研讨课“解决问题策略的复习”。既然定位于复习课,就要实现策略模块的梳理与再生,于是教师借鉴“鸡兔同笼”问题设计了一道开放性问题:拼装5辆三轮车和自行车,共用了12个车轮。三轮车和自行车各装了几辆?选择适合的方法解答。在学生分别用画图、列举、列表、推算策略完成解答后,教师追问:“这些策略之间有没有共同的联系?”话语一出,立即引起了学生的巨大反应,在学生讨论之后,师生共同归纳出它们的共同特性——“试”,而这个“试”不是胡乱的试,而是一种有方向、有方法、有目标的试,是一种在尝试中不断逼近目标的试。其背后是一种重要的数学思想——假设。假设是指先对题目中的已知条件或问题作出某种假设,然后按照题目中的已知条件推算比较,根据推算过程中出现的矛盾,不断尝试调整,最后找到正确答案[5]。如本例中的列表法与列举法就是在“试”的过程中经过多次的假设、比较和调整,最终寻找到答案;而其中的推算法不论是“假设全部是三轮车或全部是自行车,其实质也是运用假设思想。因此,当学生带着“试”的眼光重新回到各个策略的解题过程中时,策略模块就不再是独立存在的,而是相互勾联的。这样的教学不仅有助于学生加深对各个策略模块的理解,更重要的是促进学生形成更加稳定的结构化认知,进而推动策略模块的内化,做到融会贯通。
综上所述,解决问题策略模块化最大的价值是能横向突破知识领域,纵向贯通各个年级,最大化地实现学生知识体系的整体建构,让问题解决在策略的指引下变得结构化、有效化,借助解题策略之翼,提升解决问题之力。
参考文献
[1] 曹培英.跨越断层,走出误区:“教学课程标准”核心词的实践解读之七——推理能力(上)[J].小学数学教师,2014(Z1):87-94.
[2] 林传忠.整体把握教材,培养学习能力[J].福建教育,2018(23):46-48.
[3] 王恒.厘清“策略”与“方法”,落实解决问题的策略[J].小学教学参考,2019(14):63-64.
[4] 王华平.苏教版小学数学教材中“解决问题的策略”模块的教育合理性分析[J].小学科学:教师版,2017(09):121.
[5] 翟明.浅谈基于目标的模块化教学设计——“解决问题的策略——列举”的教学与反思[J].小学教学参考,2018(35):23-24.
[责任编辑:陈国庆]