领悟数学中的对称美

创新整合点

1.理实一体，教学中融入信息技术

利用动态几何软件展示轴对称和中心对称图形的特征，让学生有更直观的认识。Graph绘图软件的应用，使信息技术融入到课堂教学过程中，学生在掌握数学知识之余可以掌握软件的使用方法。课堂练习采用随机抽题小游戏的方式，在生动有趣的氛围中考查了学生的知识掌握情况。

2.四维可视，创新综合评价新方法

本节课以多元智能理论为依据，实施全员、全过程和全方位评价，并使用档案袋评价法，做到一生一档，实现数据全过程采集，同时，基于层次分析法创建成绩核算模型，构建多元多维评价体系。精准关注学生进步成长值和优秀幅度值，落实因材施教，真正实现“共评价、促成长”。

教材分析

本节课的内容选自中职教育课程改革国家规划新教材第三章“函数”第二节“函数的性质”中的第二小节《函数的奇偶性》。从整体来看，本节课体现了数形结合的思想，通过对本节内容的探究，可以为函数的实际应用做准备。

依据《中等职业学校数学课程标准》和酒店管理专业人才培养方案，按照习近平总书记“八个相统一”的要求，应落实“三教改革”，以学生为中心，以人的全面发展为导向，上承中小学已知已能，下启大学段将学将悟，以实际问题和系列活动为载体，将数学理论课与校园活动课、社会实践课联动，围绕学生专业学习和人生发展中遇到的实际问题，立体化建构教学内容，创造性地进行减、加、拓、融，搭建起数学理论与人生经验的桥梁。

学情分析

本课的授课对象为职业高中酒店管理专业一年级的学生。笔者聚焦学生特点、专业特点，从学生来源、学业基础、认知能力、学习特点、专业特性、职业面向、发展诉求七个维度对学生进行综合研判分析，发现学生已学习了函数的定义但对知识掌握不足，思维活跃但学习兴趣不高，乐于动手操作但无法将知识进行联系。因此，要充分发挥学生善于观察、乐于实践的优点，关注学生个体差异，破解学生综合运用数学理论知识解决实际问题能力不足的问题，依托系列活动，以行促知、以知促行、再行再知、知行合一，全面提升素养。

教学目标

知识与技能目标：理解函数奇偶性的概念；理解具有奇偶性的函数的图像特征，会判断函数奇偶性；会通过绘制的图像验证函数的奇偶性。

过程与方法目标：利用函数图像研究函数性质，培养观察能力；通过函数奇偶性的判断，培养数据处理能力。

情感态度与价值观目标：经历函数性质的探究过程，感受数学的简洁美，养成良好的思维习惯。

教学环境与准备

教学环境：多媒体教室、电子白板、手机等。

教学准备：教学课件、Graph绘图软件、学习通、智学网等。

教学过程

1.课前准备

教师根据学生基础和优势的差异，将学生分为六个大组（学生自主推选各自小组的组长），学生按照任务拍摄对称图形发至群里，并进行交流讨论。

设计意图：让学生在课前完成教师发布的学习任务，发现生活中的数学的美，激发对本节课内容的兴趣。

2.课中导学

（1）观察导入

教师展示图片，让学生欣赏“对称美”：①分享学习交流群中学生课前拍摄的部分照片，让学生发现生活中的对称美；②展示显微镜下雪花形成的动态图，让学生感悟对称美；③通过动态图直观地展示轴对称和中心对称图形的特征。（学生边欣赏照片，边回顾对称图形的特征）

设计意图：利用美观的图片吸引学生的兴趣，进而引出本节课的新知识。

（2）探索新知

教师引导分析对称性：将一条曲线放入直角坐标系中进行研究，然后将此函数图像沿着y轴对折，两侧的图像完全重合，得出：此函数图像关于y轴对称，对称轴为y轴。将另一条曲线放入直角坐标系中进行研究，然后将此函数图像绕原点旋转180度，旋转前后的图像完全重合，得出：函数图像关于原点中心对称，对称中心为原点。

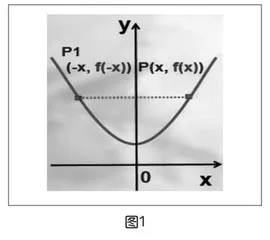
学生跟着教师的思路观察图像（如图1、图2），掌握函数图像关于y轴和关于原点对称的特征。

①引导学生分析。

当函数图像关于y轴对称时，对任意的x∈D，都有-x∈D（定义域关于原点对称），且任意点P（x，f（x））关于y轴的对称点P1（-x，f（-x））仍在图像上，纵坐标相等，即f（-x）=f（x）。

得出偶函数需满足的条件：定义域关于原点对称；f（-x）=f（x）。

②给出问题，让学生讨论，然后引导分析。

当函数图像关于原点中心对称时，对任意的x∈D，都有-x∈D（定义域关于原点对称），且任意点P（x，f（x））关于原点的对称点

P2（-x，f（-x））仍在图像上，纵坐标互为相反数，即f（-x）= -f（x）。

得出奇函数需满足的条件：定义域关于原点对称；f（-x）=-f（x）。

③非奇非偶函数：不具有奇偶性的函数。

在教师的引导下，根据函数图像的特征，得出偶函数的概念及需满足的条件；分组讨论，自主探究得出奇函数的概念及需满足的条件；熟练记忆并区分两种函数的特征。

设计意图：通过直观的图像引导学生自主探究得出结论，在活跃课堂氛围的同时，也能培养学生的思考能力，从而学习本节课的重点知识。

（3）经典例题

①讲解例1：。

解：∵定义域为（-∞，+∞），是关于原点对称

又f（-x）=（-x）3=-x3=-f（x）

∴函数为奇函数

②引导归纳“判断函数奇偶性的步骤”（如下页图3）。

③根据判断步骤，讲解例2：。

解：∵定义域为[0，+∞）

不是关于原点对称

∴函数为非奇非偶函数

学生根据偶函数和奇函数的概念，判断函数的奇偶性；在教师的引导下，归纳出判断奇偶性的步骤；利用判断步骤判断奇偶性。

设计意图：通过例题的讲解，归纳出具体步骤，并让学生将所学知识应用到具体题目中。

（4）图像验证

教师提前录制两个函数图像的制图过程，向学生展示软件使用方法；让学生通过观察函数图像的对称性来验证其奇偶性。

学生学会利用手机软件绘制函数的图像；观察图像的对称性验证函数的奇偶性。

设计意图：将数学与信息化技术相结合，激发学生的好奇心和求知欲。

（5）抽题大PK

①选择三个组分别派一名代表上台抽题，并在黑板上完成以下题目：

f（x）=2x2+1；f（x）=x-1；f（x）=2x3-x

②其他同学在纸上完成三道题，并用手机软件绘图验证。

③组长分别点评台上同学所做的题目。

组长选派代表上台抽题并完成，完成后对应进行点评；做题后利用手机软件绘图验证其奇偶性。

设计意图：利用抽题PK的方式，激发学生的做题热情；让学生自主点评，可以在发现他人问题的同时检验自己是否会做该题目。

（6）提炼精华

①学生观看微课，归纳重点；跟着教师的思路一起回顾本节课学习的重点。

设计意图：利用微课让学生对本节课的知识有系统的认识，养成归纳的好习惯。

②教师布置线上的分层作业（如图4），学生根据自身情况自主选择完成本节练习；教师根据学生作业的完成情况生成相关数据分析，在此基础上制订下节课的学习计划。

设计意图：利用分层作业的形式让学生更有效地检验学习效果；教师根据学生的作业完成情况的数据分析，制订下节课的教学计划。

教学反思

本课坚持显性教育和隐性教育相统一、理论性和实践性相统一，以建构主义、多元智能理论为指导，以丰富的资源平台为载体，依托立体教学模式，通过教学主体的调动、资源要素的调配、体系结构的调整、评价机制的调试，多措并举，理论联系实际，带动实践教学体系化、实效化、生动化、有趣化，逐步探索理论性与实践性的有机统一。针对学生信息搜索速度快、表达展示能力强的特点，设计信息整合等活动，让学生在情境任务展示中达成理论认知，在发挥优势的同时锻炼信息分析能力，增强思辨能力，在行动中增强应对本领。