影子教育能提高学业成绩吗？

［摘要］“双减”政策的实施成效受到了家长认知与决策的影响。本研究基于35项实证研究，涉及76个效应量，运用元分析教育循证方法，对家长最为关切的影子教育成效进行了探讨。元分析结果表明，影子教育对学业成绩的提升效应有限（r=0.075）；补习时长和国别差异并非影响影子教育成效的关键因素，但学科、学段、补习教师类型、测评方式对影子教育成效具有显著调节作用。具体而言，课后补习数学的效果更好；年级越高，影子教育对学业成绩的积极效应越有限；参与校内其他任课老师或校内自己任课老师开展的课外补习更为有效；若采用主观自评的学业测评方式，学生对补习效果的正向作用感知明显更大。建议理性认识影子教育，管治与疏导并置；多方协作推动优质教育资源的均衡化；继续深化教育评价改革机制，从源头上助力“双减”政策落地。

［关键词］双减政策；影子教育；学业成绩；元分析;课外补习

［中图分类号］G521［文献标识码］A［文章编号］1005-5843（2023）01-0010-08

［DOI］10.13980/j.cnki.xdjykx.2023.01.002

一、问题提出

“海淀妈妈”“虎爸”“鸡娃”“母职经纪人”是近年来社会针对家庭教育讨论的热门话题。2021年1月，《南方周末》刊发了一则《海淀妈妈“上岸”记：“顶尖再往顶尖去是很难的”》，记录了海淀妈妈如何带领儿子过关斩将拿到重点中学入场券［1］。《小舍得》《陪你一起长大》等电视剧的播出，更是将“中国式”家长以“爱”之名“鸡娃”到底的形象展现得一览无余。“剧场效应”下的课外补习俨然成为了另外一种“教育军备竞赛”。

为缓解家长群体的教育焦虑，冷却影子教育的“剧场效应”，2021年7月，中共中央办公厅、国务院办公厅出台了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》（以下简称“双减”政策）［2］。然而，家长们的焦虑似乎并未因此消减，部分家庭甚至对校外治理并不买账，试图通过招募“高端家政”“众筹拼小班”“旅行式补课”等方式继续“抢跑”。追根溯源，这一现象背后凸显的是微观家庭对课外教育投资收益的热切期待，教培行业对课外补习效果的鼓吹更是起到了推波助澜的作用。但课外补习真的能兑现承诺，促进学生学业进步吗？如果能，它的效力如何？哪个学段、哪种课程、哪类教师补习又能最大程度地帮助学生获得成功呢？现有研究并未很好地回答这些问题。本研究拟用元分析（Metaanalysis）这一高阶教育循证方法试图回答上述问题，以期为缓解家长教育焦虑，进一步助力“双减”政策落地提供实证证据。

二、文献综述

影子教育（shadow education）又称课外补习，是效仿正规教育体系，以提高学生学业成绩为目的的一种补充性教育［3］。国内外学者针对影子教育的成效开展了大量研究，但相关结论并未达成共识，目前主要有3种不同的声音：补习有用论、无效说甚至负面效应、非线性关系。

第一，补习有用论。该观点认为课外补习能够提高学业成绩。例如nal团队基于国家学生评估项目（PISA）2006报告的数据，发现课外补习1小时，数学得分可以上涨12—15分［4］。又如Park团队基于韩国教育纵向研究（Korean Education Longitudinal Study，简称KELS）数据，在控制其他变量的情况下发现不同的辅导变量（如辅导经验、辅导时间和辅导金额）对中学数学成绩的提高均有显著的正向影响［5］。再如一项基于中国教育追踪调查数据的研究同样发现，课外辅导均能提升语文、数学成绩，且课外补习对女学生、学困生、父母受教育程度更高的学生的影响效应更大［6］。

第二，补习无效说或负面效应。部分研究指出课外补习无法提高学业成绩（Smyth，2008）［7］，它更多的是一种情感和心理上的安慰剂，且这种补习无效在男性、父母职业为非精英的弱势亚群体中更为突出［8］。还有研究甚至发现课外补习会对学习成绩产生负面效应。如李佳丽的研究发现语文补习不仅不能提高学生的成绩，还会产生成绩倒退［9］。更大规模的纵向研究结果还发现在线补习、一对一家教形式均对数学成绩产生负向影响，且在控制其他变量的情况下，这一结论依然成立［10］。

第三，少部分研究发现两者关系并非简单的线性相关，而是存在一定的边界条件，包括补习时长、课程类别、师资类型、地区差异。如Liu J分析了台湾“教育委员会”收集的13 798名七年级学生的课外数学补习数据，他发现课外补习有助于提高学生的分析能力、数学成绩，但随着辅导时间的增加，这种正向效应会减少、消失最后转向负面影响［11］。刘冬冬团队基于CEPS（2013—2014）的数据发现，课外补习能够显著提高数学和英语成绩，但补习语文却无效［12］。还有研究指出，选择本校任课老师的补习不会对成绩产生负面影响，但参加非专职人员的补习却会使学生成绩倒退［13］。一项跨国研究指出，数学补习收益在不同的国家/地区间存在较大差异［14］。

综上所述，三种声音各执一词，且分别得到了实证研究的支持，这在一定程度上反映了影子教育与学业成绩间关系的复杂性与多样性。囿于单项（少量）研究结论的推广性有限，本研究拟运用元分析方法来综合上述三种不同的声音，从而获得更具普适性的结论。元分析又称萃取分析，是对同一主题的多项实证研究结论进行再分析的量化研究方法［15］。由于其具备严格而规范的实施程序，元分析也被视为教育循证改革过程中寻求“最佳证据”的一种有效手段［16］。

研究者通过检索国内外相关研究发现，“目前仅有一篇文献对该议题进行了元分析”［17］，但仍存在如下不足：一方面，未能囊括最新的实证研究结果，难以体现最新的研究进展；另一方面，该研究仅检验了成绩测量方式和年级对两者关系的影响，其他重要的诸如学科类型等关键变量的探讨未曾涉猎。基于此，本研究囊括了国内外最新研究成果，并基于已有研究的提示，进一步探讨了学科类型、补习时长、教师类型对学业成绩的调节作用。具体问题如下：影子教育能够提高学生的学业成绩吗？效力如何？影子教育成效是否受国籍、学科、学段、补习教师类型、补习时长的影响？

三、研究设计

（一）文献搜索

本研究首先在中国知网、万方数据库、维普数据库、Web of Science核心数据集、EBSCO全文数据库、SCOPUS数据库、JSTOR过刊库、ERIC数据库、PQDT学位论文库、Google Scholar、百度学术等进行大范围检索，中文检索关键词包括 “影子教育”“课外补习”“课外辅导”“校外辅导”“校外培训”，英文关键词包括“extracurricular tutorial”“private tutoring”“shadow education”“private supplementary tutoring”“cram school”等，以及相应的“shadow education and academic performance”等组合词。其次，通过浏览文献综述和相关重要文章的参考文献进一步追踪潜在的文章。考虑到该领域高质量的文章出现在2000年以后，因此，本研究将时间检索范围限定在2000年1月1日—2021年11日25日。

（二）文献纳入标准

依据研究的需要，最终进入元分析的样本应同时符合如下标准：（1）研究主题必须是影子教育对学业成绩的影响；（2）研究对象是在校中小学生，不包括大学生或社会人士；（3）研究类型必须是实证研究；（4）文献提供了可计算效应量的数据，如样本量、平均值、标准差、相关系数（r）、t值、P值、F值、卡方值等；（5）若同一文章在不同的期刊或以不同的形式出现，只取其中一种。

（三）效应值计算与编码

元分析可以呈现多种效应值（如OR值、Cohens d值、r值等），从理论上讲，每种效应值都可以表征影响效果，且不同的效应值之间可以相互转换［18］。鉴于原始数据的特点，本研究选择标准化相关系数（r）作为统计效应值。计算过程分为两个阶段，首先需要将样本相关系数进行Fishers Z转换，并用转换值进行元分析，然后把综合效应值再转换为相关系数。具体的公式如下所示：

Fisher’Z=0.5*Log［（1+Corr）/（1-Corr）］

Corr=［Exp（2*Z）-1］/［Exp（2*Z）+1）］

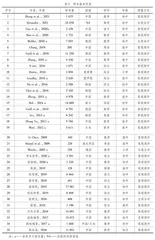
本研究将文献作者、出版年份、学习者学段、学科、国别、教师类型、测量方式等作为编码对象（见表1）。两位研究员对35个样本进行独立编码，Cohen kappa一致性系数为0.89，满足0.7的统计学要求，说明特征值编码结果有效。

（四）数据分析框架与工具

本研究采用CMA3.0（Comprehensive metaanalysis 3.0）专业版软件进行数据分析，基于35篇有效文献的数据条件，以学业成绩为因变量、影子教育为自变量，以学段、国籍、学科、补习教师类型、补习时长、测评方式为调节变量。需要说明的是，由于在编码的过程中，上述调节变量均以类别变量形式进行编码，因此本文将依次通过发表偏倚检验、异质性检验、次群体分析（subgroup analysis）方法探讨影子教育与学业成绩的关系。

四、研究结果

（一）发表偏倚检验

发表偏倚（publicationbias）是指在同类研究中，具有统计学意义的研究（阳性结果）比无统计学意义的研究（阴性结果）更容易被接受或发表。存在发表偏倚意味着该领域的研究并不完善，元分析计算出的效应值也会因此出现虚假升高现象［19］。基于此，本研究选用漏斗图（Funnel Plot）和失安全系数（FailsafeNumber，Nfs）两个经典的方法对研究样本的发表偏倚情况进行综合评估。从图1可以看出，大部分研究都分布在漏斗图上方，且相对集中在平均效应值附近，这表明元分析出现出版偏差的可能性很小。失安全系数计算结果显示（Z=20.994，P=0.000， Nfs=8 645）需要重新纳入8 645篇未发表的文献才能推翻本研究结论，因此综合判断本研究存在出版偏倚的可能性很小。（二）异质性检验

当元分析存在异质性时，通常采用固定效应模型（Fixedeffects model）和随机效应模型（Random effects model）来校正合并效应值，使得结果更为接近无偏估计。学界达成的共识是：当I2≥75%时适宜采用随机效应模型，当0≤I2≤75%时选择固定效应模型更为合适［20］。数据结果显示：Q值为455 237，且达到显著水平（P<0.001），说明各研究之间存在异质性。I2远大于75%的阈值，因此本研究使用随机效应模型对结果进行校正。

（三）影子教育对学业成绩的综合影响

本研究通过计算76项研究的效应值及使用相关系数（r）作为结果变量，得出影子教育对学业成绩的合并效应值为0.075。根据相关标准，小于0.2为极弱相关，0.2—0.4为较弱相关，0.4—0.6之间为中度相关，0.6—0.8之间为较强相关，0.8以上为极强相关［21］。因此，本研究认为课外补习对学业成绩的提高具有极弱的正向促进作用。

（四）调节变量的影响效应

第一，影子教育在不同学科中的影响。学科对影子教育的成效具有调节效应（Q=44.125，P=0.000），且各学科补习均能不同程度地提升学业成绩（见表2）。需要说明的是，本研究搜集到的部分学科（法语、科学、拉丁语）适用于元分析的实证研究仅一项，其研究结论的推广性有限，因此不予以分析。比较其余剩下的学科发现，效应值从大到小依次是数学（r=0.079）、英语（r=0.065）、物理（r=0.049）、语文（r=0.024），不过，上述学科补习效力均属于极弱正相关的范畴。

第二，影子教育在不同学段的影响。组间异质性结果表明，影子教育在不同学段的效应存在差异；年级越高，影子教育的效力越小。数据显示，3个年级阶段的补习均能不同程度地提高学生的学业成绩。比较三者的效应量发现，效应值从大到小依次是小学（r=0.297）、初中（r=0.064）、高中（r=0.053），这一结果似乎意味着随着年级的增加，补习效果会相应降低。值得一提的是，影子教育在3个年级段的效应均较小。