双新双减背景下“鸡兔同笼”问题的教学探索

基于双新双减背景，“鸡兔同笼”这一经典问题作为数学广角的内容，应如何讲？讲到何种程度？笔者认为教师需要对众多方法进行甄别和全面的考量，分清楚哪些思想方法才是最重要的，鱼与渔哪个更重要。本文通过分析枚举法、假设法、方程法、画图法、砍脚法、吹哨法的优劣与不足，倡导：重要且能迁移来解决其他问题的的思维方法要重点讲，对全体学生讲；适用面不广但巧妙的方法，不应重点讲，可作为课外拓展内容对学有余力的学生讲。同时教师要引导学生分析鸡兔同笼问题的本质，建立“鸡兔同笼”问题模型，实现知识的迁移。

一、“鸡兔同笼”问题的出处

数学名著《孙子算经》中记载了一道趣题——今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？这道题翻译过来的意思是：笼子里有若干只鸡和兔。从上面数，有35个头，从下面数，有94只脚。鸡和兔各有几只？为了更容易找到解决鸡兔同笼问题的方法和规律，不妨把数字改小一点。这种化繁为简，从简单入手的方法也是数学学习的一个重要方法，更是解决问题的一种常用策略。把数字改小后的题目：笼子里有若干只鸡和兔。从上面数，有8个头，从下面数，有26只脚。鸡和兔各有几只？

二、“鸡兔同笼”问题的解法分析

“鸡兔同笼”问题非常经典和有趣，解法也非常之丰富，通法巧法都有。归纳起来，至少有枚举法、假设法、方程法、画图法、砍脚法、吹哨法6种方法。

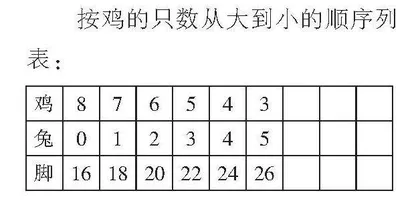
方法一：列表法（枚举法）

按鸡的只数从大到小的顺序列表：

■

此方法是将可能的情况全部列举出来，再从中找到正确的答案。此方法的优点是易理解，不易出错。缺点是当数字很大时，列举的情况会很多。虽然如此，但这种方法还是要教给学生。枚举法确实是一种能找到答案的方法。当学生没办法用其它较便捷的方法解出此题时，用枚举法找到答案，我们同样要给予肯定。这种方法，容易理解，全员都会。枚举法在解决其它问题时，往往也适用。

方法二：假设法

课本也是用了假设的方法。如果是纯算式解答，学生会看不懂或自己做着做着都搞不清自己求出来的是鸡的只数还是兔的只数。但如果配上文字，那就容易看懂了，也清楚求出来的是谁的只数了。假设全是鸡，那么脚一共有2×8=16（只），比实际少了26-16=10（只）脚。为什么会这样呢？因为我们将兔当鸡来算了。每只兔少算了2只脚。所以兔数量：10÷（4-2）=5（只），鸡的数量：8-5=3（只）。假设法也可以假设全是兔，方法类似上面。之所以要教会学生假设法，主要是因为假设法也是一种很重要、很常用的数学方法。此方法除了能解决鸡兔同笼问题，它还能用于解决其它问题。比如可以用于解决很多推理题。

方法三：方程法

解：设鸡有x只，那么兔有8-x只。依题意列得方程2x+（8-x）×4=26，整理得32-2x=26，x=3 兔：8-3=5（只）。只要学生会方程，就能够掌握此方法。此方法比较容易理解，容易掌握。求出来的是鸡的只数还是兔的只数，只要根据设来看一目了然。此方法对于“鸡兔同笼”问题百分之百适用。此外，方程法还能用于解决很多其它问题。

方法四：画图法

方法是先假设全是鸡，全都画出来，再根据相差的脚数，为“鸡”补上脚，变成“兔”，直到与题目一致，便得出正确的答案。此方法易理解，较为直观，不用画得过于复杂，简单示意就行。但此方法对于数字很大时，画起来比较耗时，也很难将此方法用于解决其它问题。

方法五：砍脚法

《孙子算经》中记载的“砍足法”新颖且奇妙，令古今中外的数学家赞叹不已。该方法是：让每一只鸡和兔都“砍去”一半的脚，则每只鸡只有一只脚，每只兔则成为“双脚兔”。这样，鸡的脚数与头数一致，兔的脚数是头数的2倍。两者脚的总数比头数多出来的数量即为兔的头数。此方法很奇妙地将复杂问题简单化。将繁化简是个好的思路，但每一种题各不同，从繁到简很显然会非常不同从而导致此方法比较难推广。

方法六：吹哨法

方法是假设每吹一次哨，鸡和兔都抬起一只脚。两次吹哨后，鸡就没有脚着地，每只兔有2只脚着地，此时地面剩下的脚数即是兔子数量的2倍。从而可求出兔的数量。此方法很妙，也很有趣。但此方法对很多题目应用不上。

三、“鸡兔同笼”问题的教学“组合拳”

那是不是6种方法都对学生讲呢？显然不是。虽然6种方法各有优点，但6种方法都讲的话时间上不允许。估计多数学生也难以消化6种方法。那么应该怎样来讲呢？对于“鸡兔同笼”问题的众多解法，教师一定要站得高，看得远，分清楚哪些思想方法才是最重要的，“鱼”与“渔”哪个更重要。

（一）有些方法要重点讲，对全体学生讲

枚举法、假设法、方程法都是非常重要的思维方法，就像三把锋利的宝剑，能把很多的数学问题斩下；又像三把万能钥匙，能把许许多多的数学问题解锁。这三种方法是通法，学生掌握了这三种方法，不但能轻松解决掉“鸡兔同笼”问题，还能迁移应用来解决许许多多的其它问题。这三种方法要讲，要重点讲，对全体学生讲。

（二）有些方法不应重点讲，可对学有余力的学生讲

画图法、砍脚法、吹哨法，这三种方法不是通法，适用范围存在很大的局限性，比较难迁移到其它题目上面来。因此，在课时比较紧的情况下，画图法、砍脚法、吹哨法不适合对全体学生讲。但这三种方法还是比较巧妙和有趣，还是有它们的存在价值。可以把这三种方法当成课外拓展的内容传授给学有余力的学生。

（三）引导学生分析问题的本质，上升到问题模型

“鸡兔同笼”问题其实是一类问题，也就是说，很多两个未知量混在一起，通过两个数量关系来表达的问题都可以转化为“鸡兔同笼”问题。例如车轮问题、租船问题等问题都可以转化为“鸡兔同笼”问题。又如和尚吃面包、答题扣分、勾兑溶液、货船载重和容积等问题也都可以转化为“鸡兔同笼”问题。

以上6个问题分析如下：

题目1：两轮车和三轮车共13辆，车轮一共28个，求两轮车和三轮车各有多少辆？分析：两轮车看成鸡，三轮车看成兔。这时每只鸡2只脚，每只兔3只脚。鸡和兔的数量之和是13，鸡脚和兔脚数量之和是28。

题目2：44人坐船去游玩，一共乘坐9艘船，小船每艘坐4人，大船每艘坐6人，求小船和大船各有多少艘？分析：小船看成鸡，大船看成兔。这时每只鸡4只脚，每只兔6只脚。鸡和兔的数量之和是9，鸡脚和兔脚数量之和是44。

题目3：一百个和尚吃一百个面包，其中大和尚每人吃三个面包，小和尚每三人共吃一个面包，求大和尚和小和尚各有多少人？分析：小和尚看成鸡，大和尚看成兔。这时每只鸡三分之一只脚，每只兔三只脚。鸡和兔的数量之和是100，鸡脚和兔脚数量之和是100。

题目4：答对一题得10分，答错一题扣6分，小明一共答了10道题，但只得到68分，求小明答对多少题？分析：答错看成鸡，答对看成兔。这时每只鸡6只脚，每只兔10只脚。鸡和兔的数量之和是10，鸡脚和兔脚数量之和是68。

题目5：现有浓度为20%和浓度为50%的酒精若干，现要配制浓度为27.5%的酒精2000毫升，求两种酒精各需多少毫升？分析：浓度为20%的酒精看成鸡，浓度为50%的酒精看成兔。这时每只鸡0.2只脚，每只兔0.5只脚。鸡和兔的数量之和是2000，鸡脚和兔脚数量之和是2000×27.5%。

题目6：一艘货船最大载重700吨，最大载货容积900立方米，现有甲乙两种货物需要航运，甲货物每吨占空间1.2立方米，乙货物每吨占空间1.5立方米，求甲乙货物各多少吨才能最大限度利用货船的最大载重和最大容积？分析：甲货物看成鸡，乙货物看成兔。这时每只鸡1.2只脚，每只兔1.5只脚。鸡和兔的数量之和是700，鸡脚和兔脚数量之和是900。

以上这些题目，都涉及两个未知量，把其中一个未知量看成鸡，另一个未知量看成兔。这时候鸡的脚不一定是2只了，可以是广义上的数（分数，小数，负数等）；同样，兔的脚不一定是4只了，可以是广义上的数（分数，小数，负数等）。如此看来，这些题目确实属于“鸡兔同笼”型问题。

这些题目虽然披着各种各样的“外衣”，但它们都有一个共同的“内核”——都是涉及两个未知量。这两个未知量以“头”的形式有一个数量关系，同时，这两个未知量以“脚”的形式有一个数量关系。鸡兔同笼问题的本质是数学中的二元一次方程组问题。鸡兔同笼问题，它涉及到的是如何通过已知条件建立方程组并求解其中的未知数。二元一次方程组的求解是初中的内容，很多小学生不会，但二元一次方程组能转化成一元一次方程来求解。不管是用二元一次方程组来求解还是用一元一次方程来求解，此类题目的本质都没有变。鸡兔同笼问题的本质搞清楚了，相应的模型也就出来了。

双新双减背景下，“鸡兔同笼”问题的教学不要仅盯着方法的量，更需要关注方法的质，还要将题目上升到模型，实现授人以渔。要引导学生分析鸡兔同笼问题的本质，建立“鸡兔同笼”问题模型，实现知识的迁移。

责任编辑  龙建刚