关注实践核心素养，促进学生经验生长

在小学数学“图形认知”的教学环节中，动手实践是关键一环。然而，当前的教学过程中存在一些问题，如过度注重动手操作而忽略了思维训练，过分强调结果的总结而忽视了方法的提炼，以及偏重结论的陈述而轻视了原理的深入探究。为了改变这些现状，本文提出教师在教学中应启发学生思考、培育核心素养、掌握知识本质，从而更好地帮助学生理解数学知识，提升核心素养，促进经验生长。

一、立足知识的生长点，培养数学抽象与逻辑推理素养

1.把握课堂核心，建立知识联系

“三角形内角和”是三角形知识学习的核心概念，对于后续知识的学习也起着至关重要的作用。在本节课中，教材提供了量、拼、折三种验证方法，但在实际教学中发现，学生在独立运用撕拼和折拼法时遇到了困难。这主要是因为他们担心图形的完整性会受到破坏，同时对规范的折叠方法掌握不够熟练。因此，教师于操作环节需发挥引导效能，助力学生构建 180°与平角的关联，借由将三角形内角转化为平角的方式直观验证结论。此过程培养了学生从具体操作到抽象出三角形内角和概念的数学抽象素养，以及通过多种验证方法进行归纳推理的逻辑推理素养。

2.引导深度探索，强化推理能力

基于以上思考，我在教学《三角行的内角和》实践操作活动中进行了如下教学尝试：

量一量。引导学生先量三角形三个内角的度数再相加。学生发现测量结果有时有误差，但接近180°。这让学生认识到测量方法的局限性，从而思考更准确的验证方法，培养了学生严谨的逻辑推理态度。

撕一撕。引导学生将三角形内角与平角联系起来，通过撕拼内角为平角来验证。学生在操作中理解了三角形内角和与平角的关系，进一步强化了逻辑推理能力和空间观念。

折一折。指导学生通过找到三角形两边中点等操作，将三个内角折成平角。学生在此过程中体会到图形的转化，深化了对三角形内角和的理解，同时提升了空间想象能力和逻辑推理能力。

二、着力教学变革点，提升直观想象与数学运算素养

1.启发学生思考，结合直观与操作

在“图形认知”的教学领域，动手操作在培养学生空间观念和几何直观方面具有重要意义。通过量一量活动，学生初步了解三角形内角和的度数情况。在撕一撕和折一折活动中，学生直观地看到三角形内角可以转化为平角，这提升了学生的直观想象素养，同时在测量和计算内角和的过程中，也涉及数学运算素养的培养。

2.规范验证方法，培养严谨思维

依循常规教学思路，尽管学生在教师引导下对验证过程予以优化，然而操作误差仍无法杜绝。教师应引导学生明晰此点，培育其严谨的科学态度。教师运用“几何画板”进行动态演示，改变三角形形状与大小，让学生观察内角变化关系。学生通过观察体会到图形变化中的不变性，增强了结论的普遍性，同时也规范了验证方法，进一步提升了直观想象和逻辑推理素养。

三、关注学生发展点，培育数学建模与数据分析素养

1.直观方法验证，积累推理经验

师：是不是任意一个三角形的内角和都是180°呢？让我们跟着动图一起来验证更多的三角形。我随意移动三角形的顶点B，你们有什么发现？

生1：我发现形状变了，内角和没变，还是180°。

师：如果把图中的顶点B一直向下拉，请你仔细观察三个内角是怎样变化的？

生：现在三个顶点都在一条线上，就不是三角形了。

教师借助移动顶点 B ，促使学生观察不同形状三角形内角和的恒定特性，进而引导学生从特殊情形迈向一般推理。

2.动态演示分析，增强数据意识

学生观察几何画板中三角形顶点移动时内角的变化，体会到图形变化中的数据关系，如内角和始终为180°，这增强了学生的数据分析意识。这种动态教学方法有效培养了学生的空间想象能力和推理意识，符合课程标准对于发展学生数学核心素养的要求，同时也在一定程度上培育了学生的数据分析素养。

四、挖掘练习延伸点，巩固核心素养

1.创设认知冲突，聚焦核心概念

活动一：三角形的拼合。教师安排学生思考两个三角形拼成一个大三角形时内角和的度数问题，由此引发学生的认知冲突。学生经实际操作与思考后，清晰认识到在拼合过程中精准确定三角形内角的重要性，这不仅强化了学生对三角形内角概念的理解，同时也培养了学生的逻辑推理素养。

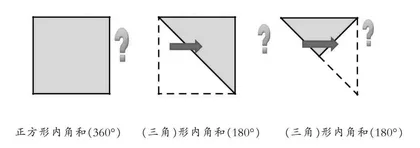
活动二：三角形的分割。教师通过正方形纸的折一折操作，让学生思考不同阶段图形内角和的变化。学生在操作中加深了对三角形内角和的理解，同时也提升了空间想象能力和逻辑推理素养，进一步巩固了核心素养。

2.拓展引申分析，内化研究方法

教师以验证直角三角形两个锐角之和为90°为例，引导学生将本节课所学的推理过程和验证方法进行迁移与内化。这不仅是对学生所学知识的全面检验，更是对其探究能力与研究精神的深度培养，巩固了学生的数学建模、逻辑推理等核心素养。通过这样的拓展引申，学生在实践中进一步领悟数学探索的精髓，积累了宝贵的推理经验，巩固了综合素养，为学生的全面发展打下坚实基础。

教育，不仅仅是课堂上的知识传授，更是一种思维的启迪与能力的培养。一节成功的数学课，应当让学生在短暂的课堂时光中收获满满，更应在课堂之外，依然保持着对知识的渴望与对未知的探索。总之，在“图形的认识”的教学中，教师应合理地组织教学过程，在教学中做到把握课堂核心、启发学生思考、培养数学素养、掌握知识本质。数学教学的意义不仅在于帮助学生提升数学素养，发展数学思维，更在于让学生在操作过程中感悟数学的本质，获得“带得走”的能力。

责任编辑韦英哲