依托棋牌游戏评价学生科学推理能力

研究表明，与电子游戏相比，棋牌游戏在教育意义方面更胜一筹。经常玩棋牌游戏的孩子在数字辨别、计数、线路排列和数字大小比较等方面表现更为出色，经常玩电子游戏的孩子则未观察到类似的积极效果。[1]教育性棋牌游戏可以提供一个实际的应用场景，让学生将理论知识应用到实际情境中。通过游戏中的任务和挑战，学生能够将学到的概念应用到解决问题的过程中，从而加深对知识的理解。结合“食物链”相关内容，我们尝试开发《捕食公园》棋牌游戏，依托游戏评价学生的科学推理能力，并衡量其科学性和有效性。

一、《捕食公园》棋牌游戏介绍

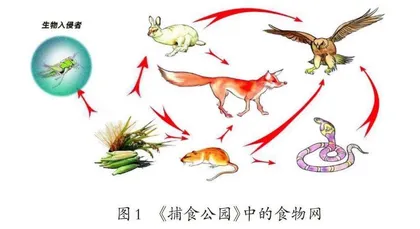
在《捕食公园》游戏中，玩家将扮演生态园长的角色，起始时拥有相同的生态群体，包括两张玉米卡牌以及各一张老鼠、兔子、蛇、狐狸和鹰卡牌。玩家的主要目标是提升生态圈的财富价值。为了达到这一目标，每轮游戏中，玩家需要挑选一张生物卡牌，并将其送入捕食公园进行捕食活动。与此同时，被选出的生物也面临着被其他生物捕食的风险。每轮捕食的结果，将根据食物网来判定（如图1）。最终，累积财富值最高的玩家将赢得游戏的胜利。

每张卡牌的中央位置都印有生物的图片，为玩家提供直观的视觉效果。在卡牌的左上角，标注有一个数字，这个数字代表着该生物所代表的财富值，是玩家在游戏中积累财富的重要依据。卡牌的最下方详细列出了每种生物的捕食结果，为玩家提供了关于生物间食物链关系的明确指示。特别说明的是，玉米卡牌的图片正下方还额外标注了玉米卡牌的功能，为玩家提供了关于玉米这一特殊生物在游戏中的独特作用的详细说明。

1.基本规则

本款游戏为三人对战模式，共设六轮角逐。游戏伊始，每位玩家均持有一张动物卡牌及两张玉米卡牌。游戏尘埃落定之时，总财富值最高者将被授予胜利者的荣耀。

每轮游戏中，玩家需精心挑选一张卡牌，并以背面示人的方式打出。随后，所有玩家同时翻开各自的卡牌，根据食物网的规则进行捕食对决。若捕食者捕食成功，不仅能将被捕食者的卡牌收入囊中，还能获得其对应牌面的财富值；若捕食者捕食失败，则意味着饥饿而亡，需将自身的卡牌上交至牌库中。对于生产者而言，若其未被捕食，则能发挥其独特功能——通过光合作用再增添一粒玉米。这意味着，生产者不仅能保留自身卡牌，还能从牌库中额外抽取一张生产者牌，以壮大自己。

2.补充规则

当一个被捕食者同时被两个捕食者盯上时，捕食者之间将展开一场激烈的竞争。在游戏中，这种竞争通过玩家间进行的石头、剪刀、布游戏来体现。胜出的捕食者将成功捕食被捕食者，不仅能将被捕食者的卡牌纳入自己的手中，还能额外获得被捕食者对应牌的财富值。失败的捕食者则能够保全自身，即保留自己的卡牌。

当一个捕食者同时面对两个被捕食者时，被捕食者之间将展开一场生存之战。在游戏中，这种竞争同样通过玩家间进行的石头、剪刀、布游戏来体现。胜出的被捕食者能够幸存下来或者得到生长的机会，即保留自己的卡牌，如果是生产者牌，还能发挥其独特的光合作用功能。失败的被捕食者则将被捕食，需将自己的卡牌交给对应的玩家。

当游戏中出现两种捕食关系，如鹰捕食兔子，而兔子又捕食玉米时，高级捕食将优先进行。也就是说，鹰会优先捕食兔子，而玉米则能够自然生长。这样的规则确保了食物链中的高级捕食者能够优先获得食物。

3.游戏进程

第1轮——正常捕食。

第2轮——生物入侵：蝗虫吃玉米。在本游戏中表现为生产者进入捕食公园立即死亡，即将卡牌上交到牌库中。

第3轮——正常捕食。

第4轮——物种灭亡。在本游戏中表现为人类毁灭性杀鼠，鼠进入捕食公园立即死亡，即将卡牌上交到牌库中。

第5轮——正常捕食。

第6轮——生物富集：有害物质通过食物链积累。在本游戏中表现为食物链顶端物种死亡，鹰进入捕食公园后立刻死亡，即将卡牌上交到牌库中。

二、学生表现的评价方法

1.评价过程

首先，我们为学生详细介绍这款游戏的玩法，并引导他们亲自体验三局。随后，我们将详细解释出牌记录（如图2）的填写规范，确保学生明白如何正确记录。接着，进行正式的测评环节，学生在玩游戏的同时，需要填写出牌记录。教师将根据表1所示的评分系统，对学生的出牌记录进行公正、客观的评分。评分结束后，为了提升学生的反思能力，我们还可以安排一节棋牌游戏复牌课，为他们提供交流心得、分享收获的机会。

2.评分系统

根据《捕食公园》棋牌游戏所考查的学生科学素养的内容，我们将评分项分为了5个方面的内容（见表1），满分为5分。

得分排名通过查看记录单上的组内排名得出。排名第一的学生可以计1分，否则计0分。

推理能体现出学生选择不同出牌类型的原因。通过查看记录单上的原因是否表达出了玩家的假设推理思维来判断计分。

算分能体现出学生是否理解了游戏规则以及出牌记录的填写要求。通过查看结果、财富值变化与最终的总财富值之间的计算是否正确来判断计分。算分实际上体现的是学生了解规则的水平。了解规则是一切游戏进行的前提条件，此环节也是对信息获取能力的训练。从学生得分率中可以看出，有超过一半的学生对游戏规则以及出牌记录的填写要求理解不到位。这实际上可以反映出这部分学生在平常的上课中，很难将教师所讲的内容理解到位。因此，我们可以通过这种测试让学生意识到自己的问题，提高他们的专注度与理解能力。

“对第2轮的理解”能体现出学生对第2轮特殊设置理解的正确与否。在第2轮生物入侵中，老鼠或兔子卡牌是劣势牌，因为玉米进入捕食公园后立即死亡，所以老鼠或兔子不能吃玉米，这将导致玩家损失2或3个财富值。在这种情况下，玉米的价值损失较小。然而，狐狸、蛇和鹰都有捕食的可能。因此，在这一轮中，打出老鼠或兔子卡牌的玩家将在这个项目中获得0分。这一项实际上反映的是学生发现规则的能力。发现规则是一个抽象、提炼的过程，在这一轮里的明规则是“出玉米立即死亡”，但并非意味着不能出玉米。因此，这一轮隐含的暗规则之一是“可以出玉米”。同时，这一轮特殊设置的暗规则是“老鼠和兔子会饿死”，若学生没有正确分析出这个暗规则，那么在这一评分项中，他们就得不到财富值。因此，教师可以在评价后，进一步开展棋牌游戏复牌课，让学生总结游戏中的暗规则，以提高他们对规则的理解水平。

“对第4轮的理解”能体现出学生对第4轮特殊设置理解的正确与否。在第4轮物种灭亡中， 老鼠或蛇卡牌是劣势牌，因为老鼠进入捕食公园后立即死亡，所以蛇不能捕食老鼠，这将导致玩家损失4个财富值。但是，除了老鼠和蛇之外的其他卡牌都有加分的可能。因此，在这一轮玩家打出老鼠或蛇卡牌，将在这个评分项目获得0分。

三、《捕食公园》棋牌游戏实施及出牌记录分析

1.被试选择

本研究的实验对象为南京市X小学六（1）、六（2）两个班的学生。学生在学习了苏教版教材第二单元第6课《有趣的食物链》之后，基本掌握了食物链的知识，可以进行本次的游戏评测。

2.预实验

（1）出牌记录

我们在六（3）班开展了《捕食公园》棋牌游戏教学，要求学生填写了《捕食公园》出牌记录，并对他们的出牌记录进行了评分。据此收集到的数据，我们使用了Winsteps对出牌记录的5个条目进行了Rasch分析。从表2可以看出，题目的信度较高，为0.92，分离度也不错，为3.39。

Rasch模型假设高水平的学生比低水平的学生有更大的概率答对某个问题。各项目拟合情况分析可以评价各个项目是否符合Rasch模型。据此可以区分出表现异常的项目。表3显示了项目信息。

通常，内部拟合指数（Infit MNSQ，简称IMNSQ）和外部拟合指数（Outfit MNSQ，简称OMNSQ）都可以用来检验Rasch模型的拟合性，IMNSQ和OMNSQ的理想值均为1，代表所测数据与Rasch模型预期完全拟合，ZSTD是两者的标准化形式，其中，IMNSQ对题目难度和学生能力水平数据比较敏感，OMNSQ对异常数据比较敏感。因此，本研究选择IMNSQ对评测方案进行分析。不同研究中，IMNSQ和OMNSQ设定不一样，一般地，当IMNSQ在0.5～1.5之间时比较适合。

测验的统计结果显示了所有项目均符合Rasch模型标准要求，其中，项目难度值范围在-1.99～2.06，难度均值为0.00，难度标准差在0.35～0.45之间，该测验的项目难度跨度较大，说明各个项目难度适中，而且具有一定的区分度。IMNSQ范围在0.82～1.14之间，OMNSQ范围是0.85～1.03之间，内部拟合度结果说明数据与Rasch模型拟合很好，所有的内部拟合度均在要求的范围内，说明测验项目本身无明显问题，而外部拟合度说明了很多项目也在范围内，本次测验项目得分受到外界环境因素的影响较小，不会引起随机误差，测量结果精准。点测量相关系数在0.5左右，实际值与期望值相差不大，说明各项目与其各自量表之间的相关度适中，不存在项目内容重复以及与记录单所测特质无关的情况，基本拟合了Rasch模型的要求。

应用项目反应理论中的单参数Rasch模型需要满足两个基本假设：①测量的内容是单维的；②项目之间是局部独立的。单维性要求测试的试题考查的是某种单一的心理特质或结构，即被试学生能否答对题目只与其某一种能力有关，忽略其他因素的影响。局部独立性则要求学生在作答某一项目时不受其他项目影响，也就是一个项目的正确与否不能影响其他项目的作答。Rasch模型的单维性是依据残差分析的基本原理进行计算的，结果通过标准残差对比图表示（如图3）。

图3展示了测验的维度，横轴代表项目难度，纵轴代表与其他成分相关的系数。当相关系数在-0.4～0.4之间时，认为项目处于一个维度，在图中用红色虚线框表示了范围。超出该范围的项目表示该项目可能测查了其他成分，即可能存在多个额外维度影响学生的回答，但是并不是所有维度都会对其产生显著的影响。相关系数超过0.7被认为是高度依赖于局部的。所有项目相关系数都在0.7以下，因此，项目的反应都符合Rasch模型的局部独立性假设，显示从该记录单中获得的数据适合用Rasch模型评价学生的棋牌游戏能力。

（2）小学生科学推理能力调查

测评问卷采用的是宋雪纯在合作问题解决教学对小学生科学推理能力影响的实践研究中使用的科学推理能力调查，[2]该调查试题主要选自TIMSS与澳大利亚国家科学教育质量监测（NAP-SL），且通过检验后具有较高的信效度。

六（3）班学生填写该调查问卷后，根据收集到的数据，我们使用SPSS对问卷所有题项进行信效度检验，得出的信度系数（Cronbach’s Alpha）为0.791（大于0.7），说明本问卷具有良好的信度。

使用SPSS对小学生科学推理能力调查结构效度进行分析，本问卷取样适切性量数（KMO）值为0.656（大于0.5），显著性（P）值为0.000（小于0.05），说明此小学生科学推理能力调查结构效度较好。

3.正式实验

在预实验验证《捕食公园》出牌记录和小学生科学推理能力调查具有一定效度之后，我们在实验班级里开展了正式实验，收集了43名学生的《捕食公园》出牌记录和科学推理能力调查，并以此作为依据分析《捕食公园》出牌记录和小学生科学推理能力调查之间的相关性，以验证《捕食公园》出牌记录在评价小学生科学推理能力方面具有一定的科学性。

本研究根据在实验过程中收集到的数据，使用SPSS对《捕食公园》出牌记录和小学生科学推理能力调查之间进行了相关性分析（见表4），可知《捕食公园》出牌记录和小学生科学推理能力调查之间存在正相关关系（r=0.352，p<0.05）。

四、结论与思考

通过Rasch分析《捕食公园》出牌记录的信度较好，且验证学生出牌记录和科学推理能力调查之间具有正相关性，我们可以得出结论：《捕食公园》出牌记录能够合理有效地作为一种过程性评价方式评价学生的科学推理能力。因此，本文为小学科学教师提供了一个棋牌游戏评价案例。

出牌记录是将学生的游戏思维显性化的一种方式，通过这种显性化的方式，教师可以探查学生的科学推理能力。游戏评价给教师与游戏开发师提供了可能的合作机会，若对游戏评价精确度的要求不高，或只希望通过棋牌游戏来提高学生的科学推理能力，教师也可以与学生一起创造或改编棋牌游戏。

虽然棋牌游戏本身不是科学活动，但它有助于学生科学思维的发展。然而，要真正发展科学思维，更直接的方式可能是通过参与实际的科学实验、探究问题、阅读科学文献等活动。本文只是推荐游戏教学的偶尔使用或作为选修课学习，以及阐明其在科学推理能力评价上的意义。

（作者：柏毅，东南大学儿童发展与学习科学教育部重点实验室教授；袁瑜，东南大学儿童发展与教育研究所、儿童发展与学习科学教育部重点实验室硕士生。）

参考文献

[1]Li X. The impact of board games and video games on children's cognitive development[J]. Journal of Educational Psychology， 2015， 107（3）.

[2]宋雪纯.合作问题解决教学对小学生科学推理能力影响的实践研究[D].杭州：浙江师范大学，2021.