基于深度学习的小学数学“做思共生”课堂实践研究

【摘 要】学生的数学学习发轫于其身体与自然世界的直接相遇与建构，“做思共生”体现了用身做、用心思，体验感悟，实现做思融合，促进学生数学理解。在教学中，引导学生经历动手操作过程，触发思考，做思共融；引导学生动手做，动脑思，重现动手操作模型，领悟内化，做思共生。通过做思共生的课堂教学，促进学生的数学学习深度发生。

【关键词】学生数学 做思共生 深度学习

“做思共生”，“做”是指基于动手的探究式学习活动，侧重于数学操作技能，如数学观察、数学实验（基本操作技能、综合运用技能）、数学制作等活动；“思”即动脑，侧重于数学心智技能，包括学生参与探究活动时的问题意识（发现和提出问题）以及动手前对问题的假设、方案的制订，动手中对现象的思考，动手后对活动的总结与反思。

“做思共生”数学教学关注“建构—探究”型教学文化的打造，认为知识是开放的体系，是动态发展的过程，具有境域性，学生要获得知识，就要获得与知识相关的经验。学生为了获得这些经验，就要走向实践、体验与操作，走向活动、综合与生活，这样，教学过程就会变得越来越丰富和完整。在教师的引领下，学生围绕有挑战性的学习任务，积极主动地、批判性地建构新知，并能够迁移运用所学知识解决实际问题，发展高阶思维能力，获得积极情感体验的学习。

观察学生数学学习的现状，学生的数学学习探究还停留在浅层次的动手活动上，动手操作看似热闹，却缺乏理性思考；过于关注学习结果，淡化过程体验；浅层活动太过频繁，缺少深层分析。教师可以通过“做思共生”的数学课堂教学实践，探索一条做与思相融、共生的有效路径，促进学生的数学理解，使学生的数学学习深度发生。本文结合“解决问题的策略—转化”教学案例来谈谈在课堂教学中践行“做思共生”，促进学生的数学学习深度发生。

一、经历动手操作过程，触发思考，做思共融

（一）课前游戏，初步思考转化现象

《义务教育数学课程标准（2022年版）》指出：数学来源于生活，生活是数学学习的源泉。当学生面对教材上枯燥和晦涩难懂的理论、概念和公式时，教师要引导学生从生活中寻找和发现它们的印记，让他们经历探索发现的过程，引发思考，获得知识；给学生提供实践机会，让学生能够充分地运用数学知识，更加深刻地理解数学的应用价值。

转化的策略在生活中的例子很多，教师可以选择学生比较熟悉的生活情境让学生感受“转化”，从学生的最近发展区来引入学习，让学习活动自然发生。教师在课前安排了一个“数铅笔”的游戏活动。

师：同学们，这里有10支铅笔（一小捆），谁能数出7支？

生1：我一支一支数出来7支。（学生边演示边说）

师：这里还有50支铅笔（一大捆），谁能数出47支？

生2：我也是一支一支数出来的。（学生动手操作，一支一支数出了47支。中途数乱两次，又集中注意力从头再数，最终成功。）

生3：我觉得可以换个角度思考，从50支中数出3支，剩下的就是47支。（学生上台操作，一遍轻松完成）

师：比较一下他们的方法，你们有什么想说的吗？

生4：虽然两种方法都能数出47支，但第二种方法换个角度数，不仅数起来快一些，而且还不容易出错。

师：换个角度思考，能让问题变得简单。在我们的生活和学习中，遇到困难时不妨换个角度思考。

在数铅笔的游戏中，让学生动手操作，学生感受到数50支铅笔数量变大，数出47支铅笔的难度增加，不仅数得慢，而且还容易数错。由此引发学生思考：数量少的铅笔一支一支数是可以的，但是数量较多的铅笔，则可以换一个角度数出剩下的几支。从50支铅笔中数出3支，剩下的就是47支。这样数方法简单，为后面教学“转化”策略积累了活动经验，作了铺垫。

（二）课中操作，深入理解转化策略

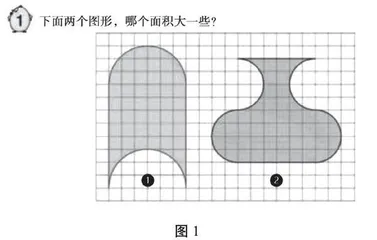
学生动手操作不是为了动手而操作，而是为了解决问题。在学生动手做之前，需要有任务驱动、目标引领，这样的操作才有针对性；动手操作后，还需要动脑思考，体验知识形成的过程，感悟抽象的数学知识。在转化策略的教学中，教师先出示例题的两个不规则图形，鼓励学生猜想它们的面积大小。

师：仔细观察这两个不规则图形，它们的面积相等吗？

（出示例题图1，学生猜想后，举手回答）

生1：我觉得第一个图形面积大，因为它上下距离长。

生2：我觉得第二个像花瓶一样的图形面积大，因为花瓶的肚子大。

生3：我觉得两个图形面积相等，但还需要验证。

师：你们能想办法验证自己的想法吗？

生1：可以使用方格纸，用数格子的方法来计算不规则图形的面积。

生2：我想可以用剪一剪、拼一拼的方法，换个角度思考。

师：请拿出学习材料包（不规则图形、透明方格纸、剪刀、直尺、画笔……），自己试一试，完成后在小组里交流你的做法。

（学生动手操作，小组交流）

生1：我是用数方格的方法计算面积的（展示自己的计算过程），第一个图形占38个满格和20个半格（不满1格算半格），38+20÷2＝48（格）；第二个图形占36个满格和24个半格，36+24÷2＝48（格）。现在看来，这两个不规则图形的面积是一样大的。

生2：我是通过剪和拼的方法，将不规则图形转化成长方形的（展示剪拼的过程）。第一个图形可以通过剪一剪，把上面的半圆向下平移8格，正好拼成长方形；第二个图形可以通过剪一剪，把下面两个半圆分别旋转180°，也拼成长方形。计算出这两个长方形面积，现在就能准确判断这两个图形的面积相等。

生3：我觉得数格子比较图形的面积有些麻烦；第二种方法，把一个不规则图形通过剪一剪、拼一拼转化成了我们学过的长方形，再计算出长方形的面积就可以精确地比较出面积的大小，这种方法比较简单。

学生通过观察图形的样子猜测两个图形面积的大小，然后借助学具操作探究并验证自己的结论，经历操作过程，促进学生深入思考。学生体会了不同验证方法，经历了不断优化方法的过程后，发现通过将不规则图形转化成规则图形，这样比较方便。这一过程丰富了学生的活动经验，促进其深入理解转化的策略。

二、重现动手操作模型，领悟内化，做思共生

（一）借助多媒体，领悟转化策略

动手做，动脑思，体验感悟知识探究的过程需要完整性，在做的基础上思，做思共融。学生经历了动手做的过程，并引发初步思考，多媒体再现操作模型，进一步思考、体验、内化知识形成的过程。

师：刚才，同学们通过动手操作验证了猜想，发现两个不规则图形的面积一样大。现在我们再次用电脑还原同学们的操作过程。

（课件演示略）

师：刚才两名同学的方法，你们更喜欢哪一种？为什么？

生：我喜欢剪拼的方法，把两个不规则图形转化成长方形，很容易看出它们的面积大小，剪拼方法计算出的结果也更准确。

师：为什么例题中的两幅图不能一眼看出面积的大小，现在能看出来呢？

生：把不规则图形转化成规则图形，就能看出它们面积的大小。这样就把复杂问题变得更简单了。

教师通过多媒体展示，让学生再次体会转化的过程。通过比较，让学生在操作后理性思考，感受到转化策略使不规则图形转化成了规则图形，就能一眼看出两个图形面积大小，把复杂问题变得简单，从而更深入地领悟内化转化策略，促进学生深度学习。

（二）沟联案例，融通转化策略

转化策略在以前的学习中涉及很多，如平行四边形、三角形、梯形、圆形的面积推导过程，就是转化策略的应用；计算异分母分数加、减法时，把异分母分数转化成同分母分数；计算小数乘法时，把小数乘法转化成整数乘法；等等。

师：其实在以前的数学学习中，就有很多时候运用了转化的策略解决问题。回顾一下，哪些数学知识用到了转化的策略？先自己思考，再把你想到的在小组里交流一下。

（学生汇报梳理的内容，整理出平行四边形、三角形、梯形、圆形等图形面积推导过程，以及计算异分母分数加、减法，小数乘法等内容，课件演示再现推导操作过程。）

师：在同学们梳理的这些例子中，都运用到了转化的策略。这个策略对解决问题有什么用呢？

生：通过转化的策略可以把新知转化成旧知，把复杂的知识变得简单。

通过沟联转化策略在以前学习中的运用，学生感受到以前的学习中已经用到转化策略，把新知转化成旧知，把复杂转化成简单，促进学生对数学知识的深度理解。

三、明确“做思共生”局限，理性运用，做思有度

“做思共生”确实让课堂因动手做、动脑思，体验感悟，促进了学生对数学的理解，让数学学习深度发生，但也存在着局限性。

（一）要“做”在需要处，不能盲从

动手做，不是解决所有数学教学问题的唯一办法，要根据教学内容和学情来确定是否真正需要让学生动手操作，不能为了操作而操作。一般是学生学习过程中，遇到了比较抽象的、难以理解的困难时，需要动手操作帮助学生理解、体验、感悟，促进深度学习。

（二）要“思”在过程中，做思共生

动手做的目的是促进学生的深度思考。学生在操作前要有操作的目标、探究的方向；动手操作完成后，积累了直观经验，形成活动体验，在“做”的过程中，要及时引发学生质疑、反思，形成正确的结论，最终经历动手操作体验、动脑思考感悟的过程，实现“做思共生”。

总之，“做思共生”旨在手脑并用，同向共进，以做促思，以思导做，不仅着眼于手脑互通、做思兼得，更落脚于“做”与“思”的彼此交融，彼此支撑。在“做”中发现，在“做”中体验，在“做”中感悟，在“做”中思考，在“做”中内化，从而促进学生数学学习深度发生，提高学生的思维品质。

【参考文献】

[1]顾长明.“做思共生”教科学的价值取向与实践策略[J].科教导刊，2021（6）.

[2]董林伟，石树伟.做数学：学科育人方式的实践创新[J].数学通报，2021（4）.

注：本文系江苏省中小学教学研究第十五期重点课题“指向数学理解的小学‘做思共生’课堂建构研究”（课题编号：2023JY15-ZA127）。