指向思维发展的跨学科教学设计与实施研究

【摘 要】数学与生活紧密相连，围绕学生在生活中感兴趣的问题来设计探究性学习。现实中的问题有时是复杂的，需要融合具体学科中的多个主题以及不同学科的知识，整体性地加以解决。在教学中，引导学生主动猜想，提升推理性思维；实验验证，体现可视化思维；小组合作，提升发散性思维；在操作中体验数学，呈现思维直观。促进学生的思维在“做数学”中发展：通过变式训练，改变思维方式；通过联系生活，提升思维能力；通过学科融合，提升思维品质，在融会贯通中促进思维进阶。

【关键词】思维发展 跨学科 数学 探究性学习

苏教版数学六年级下册第六单元的教学重点是正比例和反比例关系，本节课是在“动手做”的基础上，以反比例意义来衡量身边相关联的量，加强对反比例关系的体验。学生在一系列的亲身体验中发现新知、理解新知、掌握新知，在“做数学”中学习数学，发展思维能力。学生在探究性问题的引领下，基于自身知识经验、思维方式展开探索。探究性学习更倾向于知识点的探索和学生能力的培养，更能体现出学生的整个探究过程，使学生在这一过程中进一步获取、巩固、拓展知识。

一、操作体验，呈现思维直观

（一）主动猜想，提升推理性思维

师：今天这节课我们从数学的角度一起来探索“有趣的平衡”。说到平衡，你觉着平衡与什么有关？

生：物体的重量，还有物体到支点的长度。

师：也就是与物体的质量、到支点的距离有关。我们就从这两个角度出发，通过两个数学实验来探究平衡状态下平衡尺平衡的规律。

师：你准备怎么进行实验操作来探究平衡尺在什么情况下能保持平衡？

生1：我想在平衡尺两边相同的位置放上相同的钩码，看看是不是平衡。

生2：我还想在平衡尺两边不同的位置放上不同的钩码，让平衡尺也能平衡。

提炼：钩码质量相同，距离相等。钩码质量不同，距离不相等。

师：同学们能根据问题，想到操作的思路，非常爱思考！能不能大胆地提出你们的猜想？

生1：我的猜想—钩码质量相同，距离相等，平衡尺平衡。

生2：我猜想“左边钩码数×距离=右边钩码数×距离”。

师：我们就根据同学们的两个猜想，来开展数学实验，先来验证第一个猜想。

【设计意图】学生对问题进行思考，提出具体操作方案，一种是特殊情况的操作，一种是一般情况的操作，进而依据这两种操作思路，提出自己的猜想。教师借助问题激发学生求知欲，有计划地开展数学实验，完善知识结构，促进学生推理能力的发展，培养学生的思维能力。

（二）实验验证，体现可视化思维

活动一：探索特殊条件下平衡尺保持平衡的规律

（1）做出猜想：钩码质量相同，距离相等，杠杆平衡。

（2）实验验证：同桌合作，按照猜想挂放钩码，使得平衡尺保持平衡。

（3）得出结论：跟同桌说一说自己的想法。

收集、呈现学生的实验数据。

生3：我们发现钩码质量相同，距离相等，杠杆平衡。

师：通过同学们的实验操作，验证了第一个猜想，所以我们的猜想是正确的，从而得出“钩码质量相同，距离相等，杠杆平衡”这一结论。

活动二：探索一般条件下平衡尺保持平衡的规律

（1）作出猜想：左边的钩码数量×左边刻度数=右边的钩码数量×右边刻度数。

（2）实验验证：在平衡尺左边刻度10cm处放6个钩码，右边如何挂放钩码，使得平衡尺平衡？同桌合作，并把实验数据记录在表格中。

（3）得出结论：小组内交流自己的想法。

【设计意图】在本次活动中以平衡尺为介，通过调节钩码数量和钩码位置探究平衡现象，学生通过操作感知特殊情况下的杠杆平衡，即对称平衡，为下一步不对称平衡的操作打下基础，并获得小组合作的成就感。第二次实验是本节课的重点，也是一个开放性的实验，学生自主开展实验探究。因平衡尺的距离受孔限制，只能在5cm、10cm、15cm、20cm处加以尝试，对于其他距离的可能性无法直观检验。但部分爱思考勤钻研的学生大胆推理其他的可能性，在现有的结论中突破个例现象，从特殊到一般，思维更宽广、更有深度。

（三）小组合作，提升发散性思维

生1：我们小组通过实验操作得出，在左边5cm处要挂12个钩码，则要在右边10cm处挂6个钩码，15cm处挂4个钩码，20cm处挂3个钩码。

生2：我们发现无论左边还是右边，用钩码数×刻度数都是60，所以是左边钩码数量×左边刻度数=右边钩码数量×左边刻度数。

生3：它们乘积一定，说明钩码数和刻度数是成反比例的。

生4：我们小组还发现，刻度数变大，所需钩码数量就会变小；刻度数变小，所需钩码数量就会变大。

师：同学们来评价一下这一小组的交流分享。

生5：我觉着他们会合作，汇报的思路清晰，能结合操作用数学语言完整表达小组的发现，我要给他们点赞。

师：这一小组从纵向观察，知道了左边钩码数量×左边刻度数=右边钩码数量×右边刻度数。横向比较钩码数量和刻度数的变化情况发现刻度数和钩码数量成反比例关系，刻度数变大，钩码数量就会变小，则省力；反之，刻度数变小，钩码数量就会变大，则费力。这一小组汇报非常精彩，同伴的点评也很到位。其他小组还有补充吗？

生6：我们小组还发现了刻度数上10是5的2倍，那么钩码数上6是12的，其他也是。

师：你聚焦到了具体数的变化情况，刻度数（ ）是（ ）的几倍，那么钩码数（ ）是（ ）的几分之一。

师（出示图）：对比200g大钩码+2个20g小钩码和12个小钩码，有什么相同之处？（图略）

生：都是表示240g，质量相同。

师：钩码数量在本质上指的是钩码质量。所以我们也可以说：乘积一定，刻度数越大，钩码质量越小；刻度数越小，钩码质量越大。刻度数和钩码质量成反比例关系。

思考：活动二的发现也同样适用于活动一吗？

小结回顾：今天通过“有趣的平衡”实验，你学习到了什么？跟同学说一说。

【设计意图】本节课的两个数学实验都是通过合作的方式开展，在实验操作中，有分工、有合作、有交流。从众多变化数据中发现不变量，即乘积一定，同时横纵向对比，发现距离与质量在积不变条件下成反比例关系。同伴间的合作与相互启发使问题不断深入，组和组之间的智慧碰撞开阔了视野，也让学生享受到思维碰撞的乐趣。步步深入，层层递进，通过实验操作，学生们的体会是深刻的，思考是全面的，喜悦是发自内心的。运用希沃白板，支持学生资源生成，提高生成的质量，体现教与学的同生共长，实现深度学习。

二、融会贯通，促进思维进阶

（一）变式训练，改变思维方式

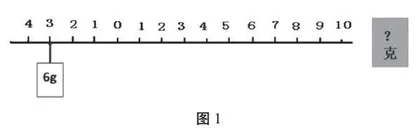
我来画：根据平衡尺左侧放钩码的质量和位置，想一想，在右侧的什么位置放多重的物体，才能保证平衡尺平衡？有几种方案？见图1。

生：1cm处挂18g，2cm处挂9g，3cm处挂6g，6cm处挂3g，9cm处挂2g。

师：同学们很棒，能有序地列举出这几种方案。这几种方案有什么共同点？

生：刻度数×钩码质量=18g。

拓展1：如果是挂在0～1的中间处呢？

生：只要想（ 0.5 ）×（ ）=18，这两个量成反比例关系，乘积都是18。

拓展2：仔细观察，两边刻度数与物体质量之间的关系，你发现了什么？

生1：右边刻度数是左边刻度数的几倍，右边物体质量就是左边物体质量的几分之一。

生2：我不是对应右边刻度数和右边钩码质量去看的，我还能发现—右边刻度数是左边刻度数的几倍，左边物体质量就是右边物体质量的几倍，如9∶3=6∶2。

生3：我还可以用比例的基本性质来理解，这里左边的3cm、6g就是内项，9 cm、2 g就是外项，也能写出比例9∶3=6∶2。

师：同学们从不同的角度去分析理解，抓住了比例的基本性质、正比例与反比例之间的联系，深入分析了它们之间的关系。

快速判断：图2中OA=4cm，OB=8cm，则铁块的质量是石块质量的几倍？

【设计意图】这一活动有三个层次，第一层次是基础训练，学生能有序列举出整数情况下，平衡尺保持平衡的情况。第二层次是打破思维方式，如果刻度数不是整厘米数呢，引发了学生的思考，改变思维方式，发现刻度数、物体质量可以是小数或者分数，只要这两个量乘积是18就可以了。第三层次用数学语言表达对两边刻度数、物体质量之间关系的理解。学生在这一环节大胆表达，思路清晰，有条理性，激发了表达兴趣。学生从不同的角度去理解，源于对知识间关系的理解和掌握，通过训练，促进学生思考能力的提升。

（二）联系生活，提升思维能力

“缺斤少两”一般指卖出的东西分量不对。请你从数学的角度来分析，商贩如何操作可以把物体的重量变大卖给顾客，从而多赚钱的，并评价这一行为。

生1：我觉着是通过减轻秤砣的质量，为了使杆秤平衡，刻度线要变大，重量就比实际重了。

生2：我知道生活中还有一种情况，有的商贩会在秤盘下面放块吸铁石，这样物体总质量就变重了。对这些黑心商贩，我想奉劝他们，只有诚信经营，才能有回头客。

生3：我听我奶奶说，有的商贩会在杆秤刻度数上做手脚。用今天学习的数学知识来解释，就是比如刻度数是5kg，但是他会稍微缩小点刻度数，显示出来就比5kg多了。

师：同学们能活学活用，把我们今天学习的知识运用到生活中去分析背后的数学原理，值得表扬。

【设计意图】数学来源于生活又应用于生活。在深度理解杠杆原理的基础上，尝试结合杆秤，分析无良商家是如何做到“缺斤少两”的呢？学生对距离与质量两要素进行交流，在语言表达的同时充分利用现代化技术，同步动态呈现秤砣变轻或杆上刻度点变密后，会使物体的实际重量变大这一现象。这类动态呈现表现得较为直观，契合数形结合的思想，紧扣积不变这一本质。最后还激烈研讨如果改变支点位置也同样可以，思维充分打开，对杠杆原理中的每个要素尝试作分析。运用希沃白板，支持学生资源生成，促进交流讨论的深入，提高生成的质量，体现教与学的同生共长，实现深度学习。

（三）学科融合，提升思维品质

站在阿基米德的立场上，要想撬动地球，需要解决哪些问题？

组织学生课后成立学习小组，开展混融性学习研究。

杠杆是简单机械中最基本的一种，杠杆知识是学习其他简单机械知识的基础。

现实中的问题往往是复杂的，需要融合具体学科中的多个主题以及不同学科的知识，整体性地加以解决。让学生在融会贯通中发展思维是“联数学”这类作业设计的理论依据。本节课有多处体现了学科融合，课始复习科学课上学的杠杆知识“认识杠杆的结构特点”，通过科学实验找到杠杆省力或费力的秘密，了解杠杆在生活中的应用，唤醒学生的记忆，为从数学的角度开展实验研究做好铺垫。后面的探究中，也会把数学发现和科学上的知识结合起来表达。数学上用相同的步骤来探究平衡尺在什么情况下能够保持平衡，用数学的知识进行分析，培养学生抽象概括能力，积累实验经验，丰富活动体验。既有学生数学学习中原有反比例知识的基础支持点，还有五年级科学省力杠杆、费力杠杆的激发点，更有初中物理阻力点、动力点、阻力臂、动力臂的延伸点，三门学科的融合，环环相扣，层层拓展，促进了学生关键能力的自由生长。

学生课后可以成立学习小组，借助书本、网络等查询相关资料，这个研究性问题体现了混融的理念，学生需要了解天文学、物理学等方面的知识来支持自己的想法。看似开放的问题，实则指向原理中的基本结构思考。同时看似完全符合杠杆原理，实则无法实现。促发学生运用多元的探究方式去尝试理解其中的奥秘，打破原有的认知，明白理论与实践并非对等，进一步突显科学、数学这一类理性学科追求的是思维的严谨性，提升思维的品质。

【参考文献】

刘善娜.单元整体视角下小学数学探究性作业的设计[J]. 教学月刊（小学版）数学，2021（10）.