在整体建构中促进模型意识的形成

《植树问题》是人教版数学五年级上册数学广角的内容。从内容编排来看，三个例题层次分明，以“解决问题”的模式引导学生通过画线段图发现规律，提取出三种不同类型的植树模型，再利用发现的规律解决生活中的简单实际问题。教学中，笔者对三个例题进行整体建构，引导学生从一个情境出发，借助数学活动发现规律，构建模型，进而举一反三，应用模型，将植树问题数学化，促进模型意识的形成，发展数学核心素养。

一、情境问题化，聚焦关键要素

教学伊始，笔者用课件展示学生熟悉的校园环境图片，并呈现情境：“作为学校的一员，我们要为校园的美化做贡献——在通往图书馆的这条小路的一侧植树。学校将这个任务交给五年级的三个班来完成，这三个班各需要种多少棵树？”随后，笔者提问：“要解决这个数学问题，需要知道哪些数学信息？”学生很快发现了问题情境中欠缺的数学信息——总长。笔者顺势追问：怎样植树，才能让校园更美观呢？是随意地种植，还是有规律地种植？根据生活经验，学生不难发现日常生活中植树的方式一般是每两棵树之间保持相同的距离。笔者由此引出“间隔”的概念。

笔者通过创设情境，引导学生挖掘解决植树问题所需要的条件，使学生在建立问题表象的过程中将情境问题化，为进一步探究植树模型埋下伏笔。

二、问题模型化，经历建模过程

1.化繁为简，整体感知

本单元三道例题的核心是棵数与间隔数之间的关系，教师要抓住“点”与“段”一一对应的关系，借助“平均分”的桥梁，引导学生自主依据经验用数学语言表达现实情境，整体感知三种不同的植树类型，形成对单元知识的结构化认知。例题解析环节，笔者首先通过图文结合的方式给出植树要求。

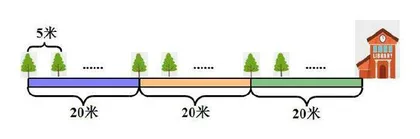
如下图，把需要植树的小路长度平均分配给三个班，每个班植树的路长是20米。一班把本班负责的路长从头植到尾；二班接着一班植树，植完本班负责的路长；三班接着二班植树，一直到图书馆。

笔者让学生理清题中的数学信息，先用学具摆一摆，再在线段图上画一画，并将自己得出的数据记录在表格中，最后用算式表示探究过程。

2.多元表征，聚焦问题

（1）摆一摆

根据植树要求，笔者引导学生用学具操作，直接得到三个班分别种了5棵、4棵和3棵的结论。为更好地引发学生的认知冲突，引导学生深度探究，笔者引导：同样都是20米，为什么棵数不一样？学生再次借助实物，通过一段一段地分开摆，整体感知三个班植树过程的区别。学生一边操作一边梳理，发现：一班从头到尾每隔5米种一棵，刚好种了5棵，完成了20米路的植树任务；二班虽然也是在20米的路上植树，但是起点位置不用种，所以只需要种4棵；三班既不用在起点位置植树，也不用在终点位置植树，所以只种了3棵。

以上教学，笔者引导学生通过摆一摆，发现每个班植树的棵数不一样，进而产生三种植树问题之间可能存在某种关联的疑惑，激发了进一步探究问题的欲望。

（2）算一算

本课的主要目标是让学生理解并掌握植树问题的数学模型。在探究路径上，笔者已经让学生通过摆实物、画线段图的方式初步得出了结果，但还需要让学生将思维的结果进一步抽象出来。笔者先通过问题“谁能用算式表示出一班学生植树的过程”，引导学生从第一种情况入手，从用图形表征过渡到用算式表征。经过探究，学生得出了两种计算方法。第一种是“20-5-5-5-5=0（米），4+1=5（棵）”。学生这样理解：起始位置先种1棵，种第2棵时减少5米，种第3棵时又减少5米，一直种到第5棵，刚好种植完20米，减了4个5，再加上起始位置的1棵，所以一共种了5棵。第二种是“20÷5=4（棵），4+1=5（棵）”。学生出现单位为“棵”的做法时，正是突破教学难点的契机。笔者没有立刻纠正学生的错误，而是引导学生分析20和5分别表示什么现实含义？为什么用除法？商4表示的又是什么呢？学生很快得出：20表示总长，5表示间隔长，按5米一段平均分，所以用除法。学生还根据除法的意义，提出商4的含义为“20米的小路，每5米分一段，被分成了4段”。学生的思路逐渐清晰，笔者进一步引导：算式“20÷5=4（棵）”中的单位应该是什么呢？学生立即将单位更正为“段”，笔者顺势引出“间隔数”的定义。

这个环节，笔者引导学生利用除法的意义建立平均分与间隔数之间的关联，打通了棵数与间隔数之间的“隔断墙”。

3.对比归纳，初构模型

随着模型的建构过程逐渐明晰，笔者抛出核心问题：要求的是种几棵树，我们却先计算分几段，那么间隔数、棵数与间隔数有什么关系呢？笔者利用线段图引导：把小路平均分成一段一段后，树种在哪儿？在图上用什么表示？笔者以此巧妙地将学生的注意力从平均分的“段”引到“点”上。随后，笔者提问：“点”和“段”有什么不一样？树种在了“点”上，平均分的却是“段”，它们之间有什么关系呢？在笔者的引导下，学生先画一个点，再画一个线段，在重复画的过程中发现点的数量总比段的数量多“1”。笔者引导学生将点与树对应，将段与间隔对应，得出了结论：小路被分成了一小段一小段的间隔，在这些小段之间的点上种树，点比段多1，所以树比间隔多1，多的即为最后一棵树。学生明确：在计算棵数时，将所求得的段数转化为与之对应的棵数，再加上多出来的树，即为所求的棵数；数量关系表示为“路长÷间隔长=间隔数，棵数=间隔数+1”。学生还将满足这个数量关系的植树情况概括为“两端都栽”。

三、模型数学化，理解模型本质

建模的本质是将数学问题“类化”，并在找到规律的基础上，类推到其他问题中。这是模型的深化过程。“植树问题”的根本在于“点”与“段”的关系，所以教师要将三个问题“类化”，让学生在三种“模型”的对比与辨析中，发现它们其实都是利用除法的意义先求20米中包含几段5米，再用“点”与“段”一一对应的数学模型表征，最后明确棵数与间隔数之间的关系，建构问题模型，使“模型”数学化。基于此，笔者引导学生自主探究剩下两个班的植树情境是否满足这种一一对应的关系，并用线段图或算式表示结论。

如下图所示，学生呈现线段图表征和符号表征两种方法，反映出学生已经具备了一定的模型意识。

接着，笔者引导学生对比分析两种植树方式在计算时的异同点。学生不难得出相同点是先求出路被分成多少段，不同点是二班的起点位置不用种植，所以树与段刚好一一对应，而三班的起点与终点位置都不用种植，所以多出来一段，没有树与之对应。笔者引导学生总结：这两种情况下，棵数与间隔数之间的数量关系可以这样表示：只栽一端时，棵数=间隔数；两端都不栽时，棵数=间隔数-1。最后，学生通过对比三种情况，总结出如下规律：无论是哪种植树情况，都是先用除法计算段数，再通过分析点与段之间的关系，找到棵数与间隔数之间的数量关系，最后得出结论。

责任编辑  张敏