信息技术助力直观想象素养提升

直观想象是高中数学课程六大核心素养之一，是学生发现和提出问题、分析和解决问题的重要手段，也是学生探索和形成论证思路、进行数学推理、构建抽象结构的思维基础。本文以“椭圆及其标准方程”的教学为例，探析现代信息技术助力高中数学直观想象素养培养的策略。

一、数学问题情境化，启迪数学思考

直观想象是借助几何直观和空间想象，感知事物的形态与变化，建立数与形的联系，并利用几何图形描述数学问题、理解和解决数学问题的素养。借助信息技术，教师不仅可以图文并茂地呈现数学问题，还能结合现实情境将空间形式或数量关系等抽象的数学知识直观地、动态化地呈现出来，把复杂的数学问题变得简明、形象， 帮助学生突破视觉和思维的限制，更好地感知数学模型的构建过程。

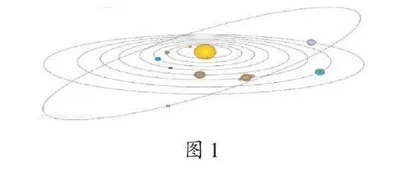
学生在日常生活中经常见到的椭圆都是静态的图形，所以他们难以将椭圆与动点的轨迹结合起来，而这正是建立椭圆概念和标准方程的关键点。教学中，笔者在情境引入环节充分借助信息技术手段，将数学问题情境化，用视频动态呈现神舟十四号载人航天飞船进入太空后运行的轨迹、各种行星在宇宙中绕着太阳运行的轨迹等（如图1），让学生在具体的情境中抽象出椭圆的几何形状，清晰地感受椭圆是动点的轨迹。

在此基础上，笔者进一步启发学生思考：神舟十四号载人航天飞船的运行轨迹是怎样形成的呢？学生在笔者启发下从数学的角度思考，了解到飞船的运行轨迹是在科学家设计的多个程序和方程的条件下形成的，初步体会到运行轨迹与方程之间的联系。

二、动态演示，发现数学本质

直观想象的核心是几何直观和空间想象，几何直观可以将相对复杂、抽象的问题“图形化”，利用图形描述问题，进而借助图形分析、解决问题。教师充分利用信息技术手段将数学问题中运动的量或轨迹还原，凸显数学问题的本质，不仅可以帮助学生理解抽象的概念，还可以充分发挥学生的想象力，让他们将“数”的变化与“形”的形成建立紧密联系。

在建立椭圆的概念时，笔者借助几何画板软件动态演示椭圆的形成过程（如图2），将“数”与“形”结合起来，引导学生观察动点M位置的变化，发现动点M到两个定点（[F1]和[F2]）的距离有哪些变化，又有哪些不变。

具体数学过程如下。

师：如上图所示，[MF1]=9.67厘米，[MF2]=3.95厘米，[MF1]+[MF2]=13.62厘米，[F1F2=]7.38厘米。在点M移动的过程中，观察[MF1]、[MF2]如何变化，它们的和有什么特点？

生1：[MF1]、[MF2]的距离一直在变化，但[MF1][+MF2]是一个定值。

师：此时，[MF1+MF2]与[F1F2]之间有怎样的关系？

生2：[MF1+MF2>F1F2]

师：[MF1+MF2]的值是动态变化的，它与[F1F2]之间可以有怎样的关系？点的轨迹怎样变化？

生3：[MF1+MF2>F1F2]，点的轨迹是椭圆。

师：如果[MF1+MF2=F1F2]，点的轨迹是什么图形？

生4：[MF1+MF2=F1F2]时，点的轨迹为一条线段。

师：[MF1+MF2<F1F2]时，点的轨迹是什么图形？

生5：[MF1+MF2<F1F2]时，不存在点的轨迹。

学生在操作演示的过程中强化了对椭圆的几何特征的认识，明确了定点即焦点、两定点间距离为焦距、椭圆上一点到两定点间距离之和为定长，并将椭圆上一点到两定点间的距离之和与焦距进行比较，探究出定长与焦距之间的大小关系对点的轨迹的影响。这样的演示操作，直观、清晰地揭示了椭圆的本质属性，帮助学生理解了椭圆的概念，感悟到概念的内涵——椭圆是平面内与两个定点的距离的和等于常数的点的轨迹。

三、直观呈现，外显数学思维

“课程标准”强调，要培养直观想象能力，就要建立“数”与“形”的联系，形成数形结合的思想。其中很重要的一个方面是以“形”直观呈现问题中的信息，让学生借助“形”的直观理解抽象的“数”，依托“形”的直观产生对数量关系及事物其他本质属性的感知，养成结合图形思考问题的习惯。

构建椭圆的标准方程时，建立坐标系是基础。怎样建立坐标系更简单呢？如图3所示，笔者运用信息技术动态演示椭圆左右对折、上下对折的过程，以及过点[F1]和点[F2]的直线的形成过程，引导学生发现过两个焦点的直线[F1F2]是椭圆的对称轴，线段[F1F2]的垂直平分线正好是椭圆的另一条对称轴，以这两条对称轴所在的直线分别作x轴和y轴，建立平面直角坐标系O-xy，用有序数对[（x，y）]表示曲线上任意一点[M]的坐标，分析点（记为[p]）在曲线上的条件，写出适合条件[p]的点[M]的集合为[p=MMF1+MF2=2a]，建立曲线方程形成的依据。

随后，学生借助静态图形，根据两点间的距离公式，用坐标表示条件[MF1=x+c2+y2]，[MF2=x－c2+y2]，用代数表示点集，列出方程[x+c2+y2+x－c2+y2=0]。处理此类问题时，通常会涉及代数与几何两个不同的领域，如果离开直观化的情境，学生很难理解其中各个部分的意义。借助信息技术展示图形，描述、分析问题，学生就比较容易理解方程中每部分与图形间的对应关系。以上教学，笔者将难以理解的代数表达式通过图形直观展现出来，引导学生发掘其中的隐藏条件，外显了学生的数学思维过程，使学生理解了方程的实际意义。

责任编辑  张敏