以『图』促学：小学数学游戏化学习策略

［摘要］ 在数学教学中，游戏化学习是儿童学习的重要方式之一。数学游戏化学习通过将数学问题融入游戏情境，能够有效激发学生的学习兴趣，促进高阶思维的发展，助力学生更好地掌握知识、积累经验以及生成学习方法，进而提升学生的“三会”核心素养。结合当下教学实际情况，教师可精心设计学习活动，巧妙融入游戏元素，并充分发挥“图”在教学中的作用，以实现其教学价值。具体而言，可采用游戏激趣，“画”图巧析；游戏生疑，“拼”图妙解；游戏促思，“变”图出新等策略与技巧，推动学生在游戏化学习中实现更好地学习与发展。

［关键词］ “图”析思维；数学游戏；游戏化学习

对于儿童而言，游戏本身具有重要的本体价值，在数学教学中，游戏化学习方式的重要性不言而喻。“游戏化学习”是基于游戏思想，将游戏元素与教育有机结合，融合游戏化思维与学习过程，借助具有趣味性、挑战性和激励性的游戏活动来提高学生的学习效果。数学游戏化学习将数学问题置于游戏场景之中，促使学生产生浓厚的学习兴趣，推动高阶思维的发展，使其能够更加有效地掌握数学知识、积累活动经验，并生成相应的思想方法，最终实现“三会”核心素养的提升。正如陈鹤琴先生所认为的，教学游戏化应以“做”为中心，即“做中教，做中学，做中求进步”。基于当下的教学实际，教师可适时地将游戏元素融入教学过程，通过游戏化设计与教学游戏化来实现其教学价值，具体可运用以下技巧：游戏激趣，“画”图巧析；游戏生疑，“拼”图妙解；游戏促思，“变”图出新，以此促进学生在游戏中实现学习与发展。

一、游戏激趣，“画”图巧析

爱玩是儿童的天性，诸如玩积木、小棒、画片等游戏深受儿童喜爱，这些游戏能够吸引儿童的注意力，激发其探究动机。教师应善于从“童玩”中挖掘数学元素，创设“玩”的教学情境，捕捉活动中的“趣点”，引导学生运用数学眼光观察生活，使其在体验游戏过程中探索世界，充分发挥游戏化学习设计的价值。同时，教师需重视直观图示的运用，将游戏中的数学问题直观化、形象化，以维持学生的学习动机。

以苏教版数学四年级下册“解决问题的策略——画图”为例，学生往往对画图的价值感悟不深，不理解在解决某些问题时为何要画图。教师可借助数形结合的方法启发学生思考，在游戏教学中，通过画图展示抽象关系显得尤为重要，这能够让学生进行深度观察，使思维更加清晰通透。

例如“玩卡片”游戏，教师设计如下活动：小明和小华共有若干张游戏卡片，小明先拿出和小华同样多的卡片给小华，小华再拿出和小明同样多的卡片给小明，此时两人的卡片数均为24张，求原来两人各有多少张卡片。

该游戏的趣味性与探索性体现在卡片数量的变化上。教师引导学生观察游戏中的“变”与“不变”，即卡片的总张数不变，而两人的卡片张数在两次游戏后发生了改变。这一问题引发了学生的思考，随后教师可带领学生通过画图来解题。

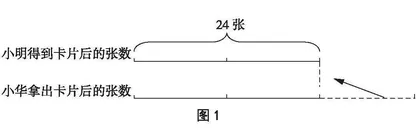
首先，从两人的卡片都是24张这一结果出发，画出第二次变化的图示（如图1）。

结合图1所示，学生能够理解其中的数量关系：小明拿出卡片给小华后，小华的张数是小明的3倍（这是理解问题的关键所在），而画片总张数是小华张数的（3+1）倍。由此，可算出小明第一次变化后的张数为：24×2÷（3+1）=12（张）；小华第二次变化后的张数为：12×3=36（张）。

其次，画出第一次变化的图示（如图2），小明拿出和小华同样多的卡片给小华，由此可得出小华原有的张数是36张的一半，进而算出小华原有的张数为：36÷2=18（张）；小明原有的张数为：12+18=30（张）。

此例表明，“玩卡片”游戏充满乐趣，学生可不断改变游戏玩法，在规则变化中丰富体验，激发并维持学习动机。教师将童玩游戏与游戏化学习相融合，让学生在“玩”中产生兴趣，引发数学思考，借助画线段图帮助学生理解数量关系，激励学生阐释游戏中的关系特征。这种源于童玩生活的游戏，有助于培养学生的数学眼光，而画线段图则可将抽象关系直观化，加深学生的理解，对学生的发展具有重要价值。

二、游戏生疑，“拼”图妙解

学生自幼儿园起便接触了大量的拼图游戏，在小学阶段如何进一步发挥拼图游戏的作用值得深入思考。古人云：学贵有疑，小疑则小进，大疑则大进。在游戏活动中，学生容易产生问题，教师应善于抓住时机，放大游戏亮点。游戏化学习设计并非单纯为了游戏，而是要在游戏中产生有价值的问题，并以问题为驱动，激励学生进行深度探究和深入思考，使游戏与学习探索紧密融合。

以苏教版数学五年级下册“解决问题的策略——转化”为例，将复杂问题转化为简单问题、将新知转化为旧知的方法多种多样。教师需运用教学智慧和点拨艺术，引导学生学会巧妙转化。其中，借助图形游戏实施转化，能够开阔学生的视野，激发其灵感。

在教学转化策略后，教师可设计如下拼图游戏：如图3所示，小华用两个直角三角形和一个长方形拼大三角形，已知一个直角三角形的一条直角边是12厘米，另一个直角三角形的一条直角边是10厘米，求长方形的面积。

学生看到该拼图游戏后会提出诸多问题，例如：

（1）长方形的长和宽都不知道，怎样才能求出长方形的面积？

（2）长与12厘米有何联系？宽与10厘米又有何

联系？

（3）若用拼成的大三角形的面积减去两个小直角三角形的面积，还缺少哪些条件？

…………

学生一时不知如何下手。部分学生这样列式：12×10÷2=60（平方厘米），这是凭感觉解题，思路不够清晰，方法明显有误；也有学生列式：12×10=120（平方厘米），但无法表达出数量之间的关系。

学生绞尽脑汁，或尝试找出长方形的长、宽，或想用大三角形的面积减去两个小三角形的面积和来求解，但均未能成功。此时教师可在学生困惑时给予启发点拨，抛出问题：能否设法将阴影部分的面积进行转化？能否从三角形、梯形的面积计算方法推理过程中获得启发？例如，是否可以用两个完全一样的三角形拼成平行四边形？

这一问题犹如一石激起千层浪！教师接着组织学生进行小组游戏，用两组完全一样的直角三角形拼图。有学生拼出如图4所示的图形，教师进而引导学生观察思考，发现图形①和②这两个完全一样的直角三角形面积相等，拼成的长方形可分成两个完全一样的大三角形；根据等式性质，阴影部分面积等于长方形③的面积，从而得知所求的长方形面积为长12厘米、宽10厘米的长方形面积。

在拼图游戏中，将已有知识经验与问题相勾连，通过构造新图形实施转化，学生的思维在问题驱动下变得更加深刻、灵活且富有创造性，借助几何直观展开深度学习，从而发展数学核心素养。实践表明，小学生的几何学习建立在“拼图”游戏基础之上，周长、面积、体积等计算方法的教学离不开图形的“拼”。

三、游戏促思，“变”图出新

随着儿童年龄的增长，智力类游戏对其更具吸引力和价值。智力类游戏与逻辑思维、儿童的创造性密切相关。数学学习中的智力活动丰富多样，富有游戏色彩且能促进学生发展的活动应由教师和学生共同发掘。教师可在数学学习中融入游戏元素，增加问题的挑战性和体验的游戏性，在提升学生思维素养的过程中发展其智力，而智力发展的核心标志是创新素质的提升，游戏学习能够提高学生的创造水平。

以“解决问题的策略——转化”教学为例，转化在学习中无处不在，尤其在组合图形面积问题中作用显著。然而，学生在求解组合图形面积时往往思路受限，教师可据此设计挑战性游戏，从中激发学生的智趣和创造精神。

例如，有这样一道数学题：如图5所示，一个正方形和一个扇形，连接AE、AF，BC=16厘米，CE=12厘米，求阴影部分面积。

教学调查显示，90%以上的教师和学生通常会按照常规方法解决该问题，如：

思路一：梯形ABCF的面积+扇形的面积-三角形ABE的面积。

思路二：正方形ABCD的面积+扇形的面积-三角形ABE的面积-三角形ADF的面积。

…………

那么，这道题的挑战性究竟何在？教师可发掘其中的游戏元素，巧妙设计闯关游戏，以问题驱动学生向更高层次的思维水平发展。

教师组织开展闯关游戏，让学生只选择一个数据来求解，比一比谁算得又对又快！儿童大多喜爱比赛和竞争，这样的设计充分体现了游戏的趣味性、探究性和创造性等特点。如何选择一个数据就能求出阴影部分的面积？学生在这一挑战性问题的驱动下展开头脑风暴和思维比拼。此时，学生联想到图形的转化，思考能否将复杂图形转化为简单图形。正当学生思维受阻时，教师适时引导，询问可以转化为怎样的图形。同学们在小组内尝试画一画、比一比，有学生灵机一动，豁然开朗，画出新图示，如图6所示。

教师在充分肯定学生的同时继续追问转化原因，学生在教师的点拨下主动建构转化思路，并通过观察发现：梯形ABCF与三角形ABE高相等（等于大正方形的边长），梯形ABCF上底CF与下底AB的和、三角形ABE的底BE都等于大正方形边长与扇形半径的和，所以梯形ABCF与三角形ABE面积相等，同时减去梯形ABCG的面积，可以得到三角形AFG与三角形CEG面积相等；利用等量代换思想，可将阴影部分面积转化为扇形面积，只需一个数据（即12厘米）即可求解。

本题作为一道游戏闯关题，其挑战性在于“只选择一个数据”，这增强了游戏的趣味性和意义，通过将不规则图形转化为规则图形，“变”中有法，“变”中有理，“变”中有利，对学生的思维和表达能力提出了更高要求。融入游戏元素后，学生的思维活跃度显著提升，在数学情境中实施游戏化设计，能够在很大程度上促进学生素养的创新发展。

有学者认为，游戏是枯燥学习活动的“提神剂”、紧张学习活动的“松弛剂”、多种学习活动的“催化剂”。游戏作为“三剂”良药，重构了儿童的学习生活。小学数学游戏化学习符合学生的年龄特点和认知规律，源于生活、基于学情、立于素养的数学游戏设计，能够促进学生生趣、有疑、深思、寻理，引发学习动机、发展思维、驱动创新、激扬精神，让学生“学会观察、学会思考、学会表达”的核心素养真正落地生根、蓬勃发展。

［本文系江苏省中小学教学研究第十五期立项课题“指向‘三会’素养的小学数学游戏化学习设计研究”（项目编号：2023JY15-L190）研究成果］

［参考文献］

［1］蔡连玉.教师的人文之旅行[M].杭州：浙江大学出版社，2017.

［2］陈鹤琴.“活教育”理论与实施[M].陈秀云，柯小卫编选.南京：南京师范大学出版社，2021.

［3］涂艳国.游戏活动与儿童教育[M].吴航主编.北京：人民教育出版社，2012.