在“分分合合”中感悟数概念的一致性

［摘要］ 从本质上讲，整数、小数、分数是一致的，都是由计数单位进行表征的。现行教材对整数、小数、分数的认识都是各自展开的，特别是小数并没有从计数单位入手。如果教师局限于利用教材开展教学，让学生感受到数概念的一致性就存在一定的困难。因此，教师需要从教材中找到合适的链接点实施教学。本文以苏教版五年级上册“小数的读写和组成”教学为例，引导学生在“分”与“合”中链接整数计数单位，在“分”与“合”中形成小数计数单位，在“分”与“合”中体验数概念的一致性。

［关键词］ 小学数学；计数单位；整数；小数；一致性

《义务教育数学课程标准（2022年版）》指出，在“数与代数”领域，要让学生初步体会数是对数量的抽象，感悟数的概念的一致性，形成数感和符号意识。从本质上讲，整数、小数、分数是一致的，但是教材一般不会点明这一点，也就造成学生难以把握数概念的一致性。那么，如何利用现有教材，让学生感受到数概念的一致性？教师需要从现有教材中找到合适的切入点实施教学。苏教版五年级上册“小数的意义和性质”单元是学生第二次认识小数，其中第一课时是“小数的意义”，第二课时是“小数的读写和组成”。笔者认为，第二课时是引导学生感悟数概念一致性的切入点。这是因为，在四年级学生已经认识了多位数及相关的计数单位，积累了一定的认数经验，而在刚刚学过的第一课时又认识了不同的小数。所以，引导学生从计数单位的产生出发，感悟整数、小数的一致性显得水到渠成。下面，将结合“小数的读写和组成”的教学片段，探讨在苏教版小学数学教材下让学生感悟数概念一致性的实践策略。

一、在“分”与“合”中链接整数计数单位

认识数的关键是理解数的建构方法，所有数都是由计数单位组成的。整数和小数都是由十进制的计数单位组成的。学生通过一到四年级的学习，已经完整经历了整数的学习过程，知道了整数的计数单位，理解了整数的产生过程。在小数计数单位教学前，先让学生回顾整数计数单位的形成方法，非常有必要。

【教学片段1】

师：回忆一下，我们学过了哪些计数单位？

生：我们学过的计数单位有个、十、百、千、万等。

师：“1”是我们认识的第一个数，进而就出现了第一个计数单位“个（一）”，那接下来其他的计数单位是怎样产生的呢？

生1：我记得是一个个数出来的，10个“一”组成了一个“十”，就产生了计数单位“十”。

师：非常好！我们从1开始，一个一个数，数到了10个“一”，就得到了一个新的计数单位“十”，接着呢？

生2：从10开始，十个十个数，10个“十”就组成了一个“百”。

生3：从100开始，一百一百地数，10个“百”就组成了一个“千”。

……

师：我们从“个”开始，10个“一”就合成了“十”，10个“十”就合成了“百”，10个“百”就合成了“千”，10个“千”就合成了“万”，个、十、百、千、万……就是我们学过的整数部分的计数单位。那么，如果我们从“千”这个计数单位开始，从左往右反过来看呢？“千”右边的几个计数单位又是怎么得来的呢？

生1：我觉得可以看作把一个“千”平均分成10份，每一份就是“百”，就得到了“百”这个计数单位。

师：这位同学真聪明，他把“千”平均分成10份，得到了“百”，其他的呢？

生2：把一个“百”平均分成10份，每一份就是“十”，就得到了“十”这个计数单位。

生3：把一个“十”平均分成10份，每一份就是“一”，就得到了“个”这个计数单位。

师：同学们思路非常清晰，从左往右看，把“千”平均分成10份得到了“百”，把“百”平均分成10份得到了“十”，把“十”平均分成10份得到了“个”。也就是说，从右往左看，每10个低级的计数单位合成一个高级的计数单位；从左往右看，把高级的计数单位平均分成10份就得到了一个低级的计数单位。

学生通过前面的学习，知道了10个“一”合成一个“十”，10个“十”合成一个“百”，10个“百”合成一个“千”，10个“千”合成一个“万”……这节课从学生最熟悉的经验入手，让学生调用自己的经验与记忆帮助理解。不过，学生在前面的学习中并没有接触到“分”，教师在学生从右往左回顾了整数计数单位的产生过程后，接着引导学生逆向思考“如果我们从千这个计数单位开始，从左往右看呢”，学生很容易就想到了“分”，把高级的计数单位平均分成10份就得到了一个低级的计数单位，“分”的经验对学生认识小数非常重要，没有“分”的思想，学生就无法从整数中的“个”突破到小数中的1/10，有了“分”的经验后，整数的概念就很容易过渡到小数的概念了。

二、在“分”与“合”中形成小数计数单位

小数与整数一样，都是基于十进位值制进行表征的，小数计数单位是整数计数单位的自然延伸与拓展，认识小数的关键就是如何从整数计数单位出发，产生小数计数单位。

【教学片段2】

师：我们刚刚认识了很多小数，你能举一个例子吗？

生：0.3、0.28、0.365。

师：小数会不会像整数一样也有计数单位呢？

生：有。

师：我们一起来研究小数的计数单位。

教师同时投影本环节的活动建议。（1）回顾：整数学习中，积累了哪些有关计数单位的经验？（2）思考：小数的计数单位会有哪些，想一想，画一画。（3）分享：小组内交流自己的想法。

师：刚才大家一起研究了小数的计数单位，哪个小组来分享一下。

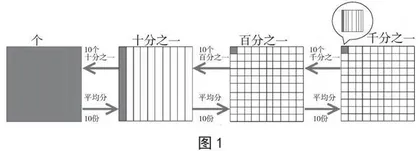
生1：把一个正方形看作“单位一”，平均分成10份，其中的一份就是1/10，1/10就是小数的计数单位。

生2：把1/10再平均分成10份，其中的一份就是1/100。

……

师：有图有真相，分数的计数单位就是这样产生的，把“单位一”平均分成10份就得到1/10，把1/10平均分成10份就得到1/100，把1/100平均分成10份就得到1/1 000……

师：那如果从1/1 000开始，从右往左看这些计数单位呢？

生：从1/1 000开始数，10个1/1 000就合成一个1/100，10个1/100就合成一个1/10，10个1/10就合成“单位一”。

师：看来认识整数时的经验在小数中同样适用，从右往左看，每10个低级的计数单位就合成一个高级的计数单位；从左往右看，把高级的计数单位平均分成10份就得到了一个低级的计数单位。

学生在“分”与“合”中回顾了整数计数单位的产生过程后，教师直接提问“小数会不会像整数一样也有计数单位呢”，让学生自然而然把小数计数单位与整数计数单位联结在一起。接着，教师提供了一个正方形作为学习媒介，并告诉学生“把这个正方形看作‘单位一’”，让学生借助正方形自主探索小数计数单位，学生很快想到了把正方形平均分成10份，继而很快得到了第一个小数计数单位1/10。可以说，1/10是从整数计数单位到小数单位的关键，发挥了承上启下的作用，有了1/10的经验，接下来的新的小数计数单位就简单了。学生顺其自然地想到了继续往下分就可以产生1/10、1/1 000这样的计数单位。当新的计数单位产生后，教师接着追问“如果从1/1 000开始，从右往左看这些计数单位呢”，学生很容易想到了10个1/1 000就合成一个1/100，10个1/100就合成一个1/10，10个1/10就合成“单位一”。如此，学生在“分”与“合”的过程中自主建构了小数计数单位（见图1）。

三、在“分”与“合”中体验数概念的一致性

计数单位是整数和小数一致的基础，通过前面的教学，学生已经深刻地感受到从个位出发，向左每10个低级计数单位可以合成一个高级计数单位；向右每个高级计数单位可以拆分成10个低级计数单位。那么，如何让学生进一步感受到数概念的一致性呢？

【教学片段3】

师：刚才，我们一起创造出了小数的计数单位，小数计数单位与整数计数单位有怎样的联系呢？想一想。

生1：小数的计数单位与整数的计数单位差不多，都是“满十进一”。

生2：都是右边的计数单位小，左边的计数单位大。

师：现在把整数计数单位和小数计数单位合在一起，先从右往左看，再从左往右看，你们发现了什么？

生：我发现从右往左看，10个1/1 000合成了1/100，10个1/100合成了1/10，10个1/10合成了“一”，10个“一”合成了“十”，10个“十”合成了“百”，10个“百”合成了“千”……

生：从左往右看，“万”均分10份成了“千”，将“千”均分10份成了“百”，将“百”均分10份成了“十”，将“十”均分10份成了“一”，将“一”均分10份成了1/10，1/10均分10份成了1/100，1/100均分10份成了1/1 000……

师：看来整数和小数属于一家人，都是由若干个计数单位组成的，而且都满足“满十进一”。

学生由于在认识整数计数单位时，已经积累了一些“分”与“合”的经验，在学习小数计数单位时就可以举一反三，应用“分”与“合”的方法。为了让学生真正体验到数概念的一致性，在学生创造出小数计数单位后，教师提问“小数计数单位与整数计数单位有怎样的联系呢”，目的在于把整数计数单位与小数计数单位的形成过程放在一起观察，学生很容易感受到无论是整数计数单位还是小数计数单位，都是按照“满十进一”和“退一作十”的规则。这样，就可以把小数和整数联结在一起，构成一个完整的系统。也就是说，通过“分”与“合”，以个位上的“一”为中心，向两侧不断延伸，从而创造出若干个计数单位，“个”的左边就是整数计数单位，“个”的右边就是小数计数单位（见图2）。

综上所述，数的概念基于对计数单位的一致性理解。在“分分合合”中感悟数概念的一致性，对于展现数学知识的本质联系，体现数学教学内容的整体性和结构化有着深远的意义。

［参考文献］

［1］巩子坤，史宁中，张丹.义务教育数学课程标准修订的新视角：数的概念与运算的一致性[J].课程·教材·教法，2022，42（06）：45-51+56.

［2］巩子坤，陈影杰，张丹.论数的概念与运算的一致性之六：如何体验运算算理、算法的一致性[J].小学数学教师，2023（05）：73-76.

柏广芹   江苏省盱眙县马坝中心小学。