基于核心素养培养背景下的三角函数的教学研究

摘 要：三角函数是最复杂的基本初等函数，通过学习和研究三角函数的基本内容和概念性质可以为解决周期性变化规律的问题打下基础。在教学中，教师要主导学习的目标和方向，积极引导学生理解概念，深刻体会周期性在函数性质中的渗透，熟练掌握三角变换以及三角函数的性质，加强数学核心素养的培养。

关键词：三角函数；核心素养；三角变换；图像性质；数形结合；周期性

中图分类号：G633.6   文献标识码：A   文章编号：1673-8918（2024）04-0085-04

三角函数是基本初等函数，它是描述周期现象的重要数学模型，在教学和其他领域中都具有重要的作用。从高中三角函数的教学内容来看，渗透了逻辑推理、直观想象、数学计算等核心素养，学习三角函数对发展学生的全面素养具有非常重要的意义。

学习目标和素养能力的培养，特别强调以下几点：第一，把角放在坐标系中研究，使对角的研究有一个统一的载体，通过对各种角的表示法的训练，提高学生分析、解决问题的能力。教学应始终贯穿着旋转、对称变换及数形结合的思想方法，要重视数学思想方法的渗透。第二，三角函数的图像与性质教学应该从以下几个方面入手：①教周期函数的一般研究思路和方法。三角函数是刻画周期现象的函数模型，应教会学生研究周期现象的一般方法：在一个周期内研究性质，该函数在其他周期内重复基本周期区间的性质；以周期性为抓手，真正理解三角函数的单调性、对称轴、对称中心的性质。②教“真难点”，通过三角函数的图像变换，理解掌握正弦型、余弦型、正切型的函数的图像性质。通过图像变换的学习，培养从特殊到一般，从具体到抽象的思维方法，从而达到从感性认识到理性认识的飞跃。③教数形结合，应重视单位圆的教学，单位圆不仅仅说明了三角函数定义和绘制图像，还可以借助单位圆的直观特点，来很好地帮助学生理解正弦函数、余弦函数的周期、最值、诱导公式、单调性、奇偶性等性质，又能更好地反映问题本质。

下文对三角函数知识追本溯源，引导学生领悟技巧和方法。首先，终边角、区间角的表示，知识都是起源β=α+k·360°，k∈Z这个公式的知识形成（表示形式不唯一）。熟练掌握把任意角化为α+k·360°，k∈Z且0°≤α<360°的形式。通过角的合并，记住以下规律：①终边在一条射线上时，其角的集合为：｛α｜α=θ+k·360°，k∈Z｝；②终边在一条直线上时，其角的集合为：｛α｜α=θ+k·180°，k∈Z｝；③终边在两条相互垂直的直线上时，其角的集合为：｛α｜α=θ+k·90°，k∈Z｝。上述公式中的θ表示终边落在该直线（射线）上的任意角。记住这些终边角的位置，并学会用旋转的方法来表示终边角和区间角。比如k·180°+135°，k∈Z就可以看作是k·180°，k∈Z终边角（x轴）沿逆时针旋转135°得到的。

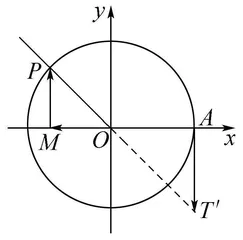
三角函数定义，搞清楚自变量是角的弧度数；三角函数值只和角的终边位置（从原点出发的一条射线）唯一相关，当角的终边所在象限有多种情况时，必须分象限来讨论。如图，在坐标系中引入了单位圆，我们就可以用正弦线、余弦线、正切线来表示一个角的正弦值、余弦值、正切值。

余弦线、正弦线和正切线。这里体现了数形结合思想，以“形”显“数”，方向和坐标轴正方向同向为正，方向和坐标轴负方向同向为负。三角函数线的引入，让三角函数值变得直观起来，有了三角函数线，我们就可以动态地观察三角函数值的变化和变化规律，利用三角函数线来解三角方程和三角不等式非常便利。

解：画出三角函数线如图。

公式的常用变式如下：

1. tanα±tanβ=tan（α±β）（1tanαtanβ）；sin2α

分析：由于β=（α+β）-α（用给值角来表示求值角），根据已知利用两角差的正切函数公式即可计算求解。

（2）（1+tan19°）·（1+tan26°）=    。

分析：先把所求展开，再根据两角和的正切的变形即可求解。

解：因为（1+tan19°）·（1+tan26°）

=1+tan19°+tan26°+tan19°tan26°

=1+tan（19°+26°）（1-tan19°tan26°）+tan19°tan26°

=1+1-tan19°tan26°+tan19°tan26°

=2；

故答案为：2。

A，ω，φ，三个特征参量，每种图像变换前后的解析式只改变一个特征参量，相位变换前后的解析式只改变φ，周期变换的前后解析式只改变ω，振幅变换的前后解析式只改变A，通常的变换顺序为：相位（平移）变换→周期变换→振幅变换。

1. 求解三角函数的值域（最值）常见四种类型：

（1）形如y=asinx+bcosx+c的三角函数化为y=Asin（ωx+φ）+c的形式，再求值域（最值）；

（2）形如y=asin2x+bsinx+c的三角函数，可先设sinx=t，化为关于t的二次函数求值域（最值）；

（3）形如y=asinxcosx+b（sinx±cosx）+c的三角函数，可先设t=sinx±cosx，化为关于t的二次函数求值域（最值）；

（4）形如y=asin2x+bcos2x+csinxcosx+d的三角函数，“降幂化一”化为y=Asin（ωx+φ）+c的形式，再求值域（最值）。

5. 由图像写函数的表达式的问题。

y=Asin（ωx+φ）+h类型，一般先求h，再求A，再由T求ω，最后求φ。

（2）A=M-h；

（3）再由T求ω；

（4）最后用求φ方法求φ。

解析：因左右平移变换是对自变量x本身“左加右减”。故应先把两函数化为下列形式：

α，即：

为了更好地落实核心素养的培养目标，教师要积极地引导学生进行深度学习；所谓深度学习，就是指在教师引领下，学生围绕具有挑战性的学习主题，全身心积极参与，体验成功、获得发展的学习过程。深度学习已经成为新时代高中数学教学得以更好发展的必然途径，也是学生学习能力提升和核心素养培养的坚实保障。教师在三角函数这一部分的教学中，围绕教学重点难点，可以组织探究式教学活动，引导学生在活动中实现自主探究与思考，由表及里，从而有一个深入、充分、多元和丰富的学习体验，达到锻炼自身数学思维的目的，让核心素养的培养得到有效落实。

参考文献：

［1］林丽娟.深度学习与核心素养的融合——高中数学活动课教学的新思路分析［J］.高考，2023（28）：9-11.