精研细磨预学单，锻造数学学习关键工具

【摘 要】本文探讨小学数学教学中预学单的应用。通过对教学效果的深入研究，提出了四个设计预学单时需要遵循的原则。依托四个原则，根据不同模块的知识教学，给出了四种预学单的案例类型。

【关键词】预学单 设计原则 类型

预学单具有把握学生学情，让思维可视化等优点，起到让学生提前介入学习内容，搭建起链接课堂桥梁的作用。教师根据不同的知识模块设计数学预学单，有针对性地选用设计类型，以期提高学生的学习效果。

一、提炼原则，树立设计的标杆

（一）遵循以生为本的主体性原则

预学单要由“知识本位”逐步向“学生本位”迈进。教师应注重服从学生的学习需要设计预学单，并遵循以生为本的原则将学生置于学习的核心位置。教师可根据学生的兴趣、能力和学习风格设计预学单的内容，激发他们的学习动力和积极性。另外，还可以通过量身打造的预学任务，引导学生通过探索、合作，共同构建数学知识，有助于培养学生的团队合作和沟通能力。

（二）遵循以研启智的思辨性原则

预学单作为一种教学工具，可以弥补课堂时间短导致学生思考不够深入的缺陷。通过预学单可在课前引导学生充分思考，这有助于他们在思辨中启发认知。因此，预学单要贴近生活，突出数学的应用价值，从基础的数学概念到逻辑推理及创造性问题。其中的方法指导要注重引导学生提出问题、解决问题，鼓励学生充分交流观点，经历、体验习得知识的全过程。而具体设计要多设置启发式问题，吸引学生主动探索，寻求方法背后的逻辑和原理。

（三）遵循以线概面的简洁性原则

小学生的学习时间和读取信息能力有限，预学单的内容过于繁杂，容易使学生产生条理不清、重点难抓的感觉，而简洁的设计方便学生围绕主线展开预学。因此，预学单的设计要从“面面俱到”转向“有所侧重”，注重培养学生的关键能力。以线概面就是要做到突出重点、抓大放小，其中应有合理的内容组织和结构，清晰的任务划分和逻辑顺序。知识存在递进关系时，设置问题应指向基础知识为宜，为后续更具挑战性问题的理解和解决作铺垫。

（四）遵循以疑导教的反馈性原则

预学单的设计应遵循“掌握疑问、注重反馈”的原则，体现在能够评估学生的理解水平，包括了解哪些概念被理解，哪个知识点存在理解误区，以及学生的学习策略；还可以揭示学生的学习差异，了解他们的需求，从而有针对性地展开教学。

二、裁体类型，引领实践的导航

（一）模仿理解型

模仿理解型的预学单，指的是一些较为简单、有据可依的知识，学生可以通过自学得到形式上的习得。比如列竖式计算、脱式计算、小数或分数的四则运算等，基本可以设计这种类型的学习单。这些知识的学习往往可以按步骤进行，即模仿—理解—习得。通过模仿，学生掌握表征，而后进入理解阶段，迁移背后的原理和规律。最终，在理解的基础上，学生相对清晰地获取知识。以人教版四上“三位数乘两位数”的预学单为例，设计如下预学单。

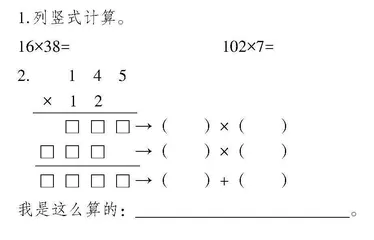
1.列竖式计算。

16×38= 102×7=

2.         1 4 5

× 1 2

□  □  □ →（ ）×（ ）

□  □  □       →（ ）×（ ）

□  □  □  □ →（ ）+（ ）

我是这么算的： 。

以“两位数乘两位数”“三位数乘一位数”的旧知为基础，教师在预习单中让学生模仿格式，再理解算理、算法。习题2就是模仿，说说怎么算就是引导学生深入理解。在新课的教学中，教师可以在预学单基础上，让学生结合情境，说说竖式中每一步具体表示什么意思。这样的预学单促使教学进阶有度、步步深入，与学生的学习过程、认知发展规律是相适应的。

（二）操作探究型

操作探究预学单可引导学生通过实践操作认识数学概念，培养其发现问题、解决问题的能力。大部分知识仅靠学生的读写想象是无法真正理解。《义务教育数学课程标准（2022 年版）》从动手实践和自主探究两个方面强调培养学生良好的学习习惯。以人教版六上“圆的认识”为例，设计以下预学单。

探究一：1.请你借助身边的物品画一个圆，并剪下来。2.我思考，这个物品内含圆这个形状，这样设计的好处： 。

探究二：1.对折一次剪下的圆，画一条黑线。2.再对折一次，画一条红线。展开我发现，这两条线长度有这样的关系： 。

探究三：再从其他方向对折两次，分别再画出一条黑线和一条红线，1.把黑线和黑线对比，我发现： 。2.红线和红线对比，我发现：   ；3.四条线有 个交点。

这份预学单以一系列操作为主，预学单中没有明确给出直径、半径、圆心的相关概念和关系，通过精心设计的操作任务，激发学生对圆的好奇心和探究欲望，引导学生探究圆的特性。课堂教学以预学单的实践操作为基础，教给学生关于圆的相关概念和关系，从而引导学生从浅尝辄止的记忆走向深层次的学习。

（三）梳理串联型

梳理串联型预学单对于一些复杂概念或图形的推理至关重要，它构建了认知框架，为学生学习新知提供了方法。通过梳理串联，学生能更有条理地掌握数学知识，为解决复杂的数学问题打下基础。以人教版五上“梯形的面积”为例，设计如下预学单。

回顾一：平行四边形的面积= 。如何转化成已知图形进行公式推导，请你画一画，写一写。

回顾二：三角形的面积= 。如何转化成已知图形进行公式推导，请你画一画，写一写。

梯形的面积与三角形面积的联系尤为紧密。本课不仅要记住公式，更要在已学图形的基础上进行方法迁移，推导出梯形的面积计算公式，进一步培养学生的推理意识和创新意识。因此，教师通过预学单，让学生梳理平行四边形和三角形的面积推导方法，做到有法可依。这种基于梳理串联的学习，为根植数学思想方法提供了稳固的基础。

（四）调查体验型

数学源于生活。教师要提供调查和体验的机会，引发学生对数学的兴趣和好奇心。这类预学单适用于统计与概率、综合与实践模块，引导学生在课前调查体验、收集数据、自主探索。调查体验的过程可以激发学生的主动学习意识，加强对数学应用和意义的理解，也有利于教师了解学生思维和理解水平。以人教版五下“折线统计图”为例，设计如下预学单。

调查一：请你和小伙伴搜集华为手机全球出货量信息。

[年份 2015 2016 2017 2018 2019 全球出货量 ]

调查二：请你和小伙伴搜集苹果手机全球出货量信息。

[年份 2015 2016 2017 2018 2019 全球出货量 ]

（1）2020年9月，美国为何断供华为芯片？

调查三：继续搜集华为手机全球出货量信息。

[年份 2020 2021 2022 2023 全球出货量 ]

（2）断供后，华为手机业务受到的影响怎么样？

借现实问题，以明确的目标为驱动设计预学活动，倡导学生运用信息技术调查、体验。搜集和整理数据是统计的基础活动，虽然占据时间多，但属于有意义的实践活动。在预学单的基础上，教师在课堂上生成折线统计图，引导学生综合前期所得开展深入分析。在此过程中，学生深刻体会到统计只是知识，分析才是智慧，统计意义随之彰显。

（作者单位：福建省厦门市同安区新星小学

责任编辑：宋晓颖）