蓄势生长 回望延展

［摘 要］过程性教学具有独特的优势，其更多地关注教学过程的构建，让学生经历知识的发生、发展过程，经历定理、法则的探索过程，从而实现知识的整体建构和自然生长，以及对学生数学思维的培养。文章从操作层面阐述初中数学过程性教学模式的探析与思考。

［关键词］过程性教学；初中数学；探析；思考

［中图分类号］    G633.6        ［文献标识码］    A        ［文章编号］    1674-6058（2024）23-0011-04

一、初中数学教学现状

《义务教育数学课程标准（2011年版）》指出：教学活动是师生积极参与、交往互动、共同发展的过程。数学课堂应该是激发学生兴趣［1］，调动学生学习积极性，引发思考的活力课堂。但目前的初中数学教学中仍存在以下不足：

（一）重刷题轻思想

在初中数学教学中，部分教师注重引导学生刷题，虽然刷题在一定程度上有助于巩固知识，但完全靠刷题是很难培养学生的数学思维和创新能力的。因为刷题是机械、重复的，学生缺乏对知识的探索与思考，很难真正掌握题目中的数学本质和数学思想方法。

（二）重局部轻整体

在初中数学教学过程中，部分教师着重某个知识点或某个方法的应用，并未顾及学生的长远发展，很少关注数学知识的研究过程、研究方法。在这样的教学中，学生可能理解了单一知识点，但在综合运用知识解决问题的时候却困难重重。

（三）重讲授轻探究

在初中数学教学中，部分教师注重知识讲授，并未注重学生的自主探究。学生没有经历知识的发生、发展过程，没有经历定理的形成过程，对知识的理解不透彻。这样的教学，不利于学生自主探究能力的提升，不利于数学思想方法的形成。

二、初中数学过程性教学探析

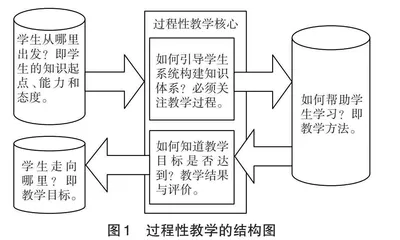
过程性教学以知识的发生、发展和认知形成的内在联系为线索，使学生积极参与、自主学习、主动探索知识，发展其探索能力［2］。过程性教学具有独特的优势，它从学生的知识起点出发，更多地关注教学过程的构建（如图1），实现学生的学与教师的教和谐统一。

师生间的信息传递体现在课堂、教学和学习上。教师应结合过程性教学信息传递特性，合理、科学地设计教学过程，让其更具有针对性和高效性，让学生在多样化的教学过程中学到知识。

教师视角下，过程性教学强调教学的主导性；学生视角下，过程性教学强调学习的主动性，并不是传统学习过程中的被动吸收知识；知识层面上，过程性教学强调学习是一种探索性过程，注重知识的生长和整体建构，从而实现教师、学生、知识三者的相互促进（如图2）。

过程性教学中，教师要关注教学过程，具体流程如图3所示。

下面以“一元二次方程解法（1）”为例 ，探讨初中数学过程性教学的实施策略。

（一）蓄势：课前预习，诊断学习起点

课前预习是过程性教学的一个重要环节，它关注学生的知识起点、学习能力和学习态度，是引领学生高效学习的重要组成部分，也是把脉学情的重要方式。课前预习可重点从以下三个方面入手：

1.利用学习清单，培养学习习惯

【学习清单】阅读课本P29—30。

（1）思考并尝试完成课本P29的合作学习活动。

（2）整式的因式分解方法有哪些？请写下来（记不全的同学可以查阅七年级课本）。

（3）自学课本例题（有疑问的，请查阅相关资料，仍无法理解的，请做好标注）。

设计意图：在学习清单中标出弹性要求，一方面鼓励不同层次的学生在自己力所能及的范围内积极思考，主动查阅相关资料，养成良好的学习习惯；另一方面，引导学生为后续的课堂前测及有针对性地听课做好准备。

2.分层课前检测，诊断自学效果

【课堂前测】

用因式分解法解下列方程。

基础题：（1） [x2+x=0]；（2） [x2=3x]；（3） [x2-25=0]；（4） [x2+9=-6x]。

提高题：（1） [（x-2）（2x-3）=6]；（2） [9x2=（x-1）2]；（3） [（x-2）2=2x（x-2）]；（4） [x2-22x=-2]。

拓展题：[（x2-1）2-5（x2-1）+4=0]。

设计意图：学生读懂了课本，并不一定意味着掌握了相关知识，检测是最直接明了的方法。通过课堂前测，了解学生的自学情况，掌握真实学情，为精准教学的实施奠定基础。课堂前测的设计始终围绕“弹性学习”展开，分三个不同层次，选题时紧扣教材，结合教学重点、难点、易错点，有效整合教学内容。三个层次用意分别为：基础题适合后进生，其难度与课本例1相当；提高题适合中等生，后进生在得到有效指导后也可以完成；拓展题适合学有余力的学生，中等生在获得帮助后可以完成。

3.收集前测作业，定位教学预设

收集前测作业，全面了解学生的自学情况，根据本节课的重难点收集典型错误并分析原因，精准把握学情，做好教学准备。

（二）生长：课中练习，促进目标达成

课堂中教师依据前测情况，引导学生对典型错题进行探究学习。按照题组的难易程度，分段递进组织教学，使得每个层次的学习目标更明确，任务完成情况更清晰。特别是在课始马上进行基础题组的教学，更容易吸引注意力容易分散的后进生。

在组织形式上，通过“大家来找茬”活动激发学生兴趣，以独立思考、小组合作、班级汇报等多种形式引导学生归因纠错，促进学生正确建构新知识。

通过基础题组和提高题组促进教学目标达成。

1.基础题组学习

（1）多重对质，解构原概念

①对质PK1：学生之于新知

错题1： [x2=3x] 两边同除以[x，得x=3]。

生1：我认为方程两边不能同除以[x]，如果[x]等于0，则没意义。

生2：我也认为方程两边不能同除以[x]，否则方程少了一个解。

②对质PK2：学生之于教师

师：那么正确解法是什么呢？（一个学生展示正确解法，略）

师：由此我们能得出什么结论呢？

③对质PK3：学生之于学生

生3：对于[x2=3x]型一元二次方程，应移项再提取公因式求解，不能同除以[x]。

生4：[x2=3x]，移项并整理得[x（x-3）=0]，所以[x=0]或[x-3=0]，将一元二次方程转化为两个一元一次方程。

（2）思维助手，构建新思想

①引入旧知，唤醒元认知

错题2：[x2+9=-6x]，移项得[x2-6x+9=0]，   [∴（x-3）2=0]，[∴x=3]。

生5：第一步移项符号错了，而且方程少了一个解。

师：那么正确解法是什么呢？（一个学生展示正确解法，略）

②游戏互动，激发求知欲

师（追问）：按目前所学的方法，由[（x+3）2=0得x=-3]，你依据什么知道方程少了一个解呢？

生5：我们看到课本第30页最后一行的标注。

师：这组同学阅读课本时非常细心，确实，数学阅读与其他学科的阅读不同，数学知识概括性强，每一句话都有特殊意义，对数学阅读我们一定要多细心、多思考。请同学们仔细阅读课本第30页最后一行的标注，并将它画起来，后面我们将会继续探究为什么要这样表述。

师：实际上[（x+3）2=0]表示[（x+3）（x+3）=0]，所以[x1=-3]，[x2=-3]，为方便表述写成[x1=x2=-3]。

师：如何将一元二次方程转化为一元一次方程？

生（齐）：因式分解。

③承前启后，提升新思想

师：通过上述例题，你能归纳因式分解法解一元二次方程的一般步骤吗？（生答略）

题组总结：对于[x2=3x]型一元二次方程，应移项再提取公因式求解，不能同除以[x]。对于 [x2+9=-6x]，应注意移项变号得[（x+3）2=0]，将两个相等的实数根写成[x1=x2=-3]，不能漏根。一元二次方程的求解步骤：先将方程右边化为0，再将左边的代数式因式分解，转化为一元一次方程，再求解。

设计意图：针对后30%学生，通过小组合作学习及一对一或多对一的结对帮扶，确保其扎实掌握知识。小组汇报中，让后30%学生充分发言交流。通过该组题的学习交流，基本达成用因式分解法解一元二次方程的课程要求。通过阅读课本、查阅资料、自主练习、同伴互助等多种途径，学生逐步实现了从模仿到会做、会讲的转化，提升了课堂学习的获得感。

2.提高题组学习

（1）正确时“挑刺”，追问促深思

错题3：∵[（x-2）（2x-3）=6]，∴[x-2=0]或[2x-3=0]，∴ [x1=2]，[x2=32]。

师：本题的错误原因是什么？

生6：不能得到[x-2=0]和[2x-3=0]，因为方程的右边是6而不是0。

师：观察力非常敏锐。在我们前面得出的[AB=0]，[A=0]或[B=0]的结论中，方程的右边必须是0。这题该如何改正呢？请出示你们组的正确解法。（解法展示略）

师：由此我们可以得到的解题经验是什么呢？

生7：只有[AB=0]，才可以得到[A=0]或[B=0]。如果方程的右边不是0，可以进行化简整理。

（2）错误时“潜伏”，追问诱反思

错题4：[9x2=（x-1）2]。

∵原方程可化为[9x2=x2+1]，∴[8x2=1]，∴[x2=18]，∴[x1=24]，[x2=-24]。

师：本题错在哪儿呢？

生8：等号右边运用完全平方公式时，漏了[-2x]。

师：非常好。对于公式、定理、基本事实等，我们要注意在理解的基础上正确记忆、运用。那么本题的正确解法是什么呢？哪个同学来展示一下你们组的解法？

生9：原方程可化为[9x2=x2-2x+1]，移项得[9x2-x2+2x-1=0]，即[8x2+2x-1=0]，则有[（2x+1）（4x-1）=0]，[2x+1=0]或[4x-1=0]，∴[x1=-12]，[x2=14]。

师：这是用了什么方法进行因式分解？

生9：十字相乘法。

生10：我认为还有第二种解法，即移项得[9x2-（x-1）2=0]，∴[3x+（x-1）3x-（x-1）=0]，∴[（4x-1）（2x+1）=0]；∴[x1=14]，[x2=-12]。

师：课本例题中有类似解法吗？这种解法用了什么公式进行因式分解呢？

生10：课本的例2（2）用了平方差公式进行因式分解。

师：涉及的数学思想方法是什么呢？

生10：整体思想。

生11：我们组还有不同的解法。（学生展示如下）

∵原方程可化为[3x=x-1]或[3x=-（x-1）]，

∴[2x=-1]或[4x=1]，

∴[x1=-12]，[x2=14]。

师：这种方法看上去很简单，它的依据是什么呢？

生11：平方根的意义。

师：真是太了不起了！我们知道如果[x2=a]，则[x=±a]。这种方法运用了平方根的意义、整体思想，是基于教材又高于教材，对知识进行巧妙融会贯通。下节课我们进一步研究这种解法。