提升学生直观想象素养有效策略探析

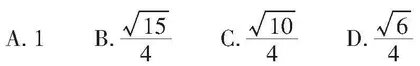
［摘 要］ 直观想象在数学学习中扮演桥梁角色，它能连接现实与抽象世界、数与形，能帮助学生简化复杂问题并有效解决问题。鉴于新课标对数学教学要求的提高，提升学生直观想象素养成为教师的重要任务。文章基于教学实践，提炼了几点提升学生直观想象素养的策略。

［关键词］直观想象素养；策略；数形结合

［中图分类号］    G633.6                ［文献标识码］    A                ［文章编号］    1674-6058（2024）32-0018-03

《普通高中数学课程标准（2017年版2020年修订）》（本文简称《数学课标》）指出，直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养。主要包括：借助空间形式认识事物的位置关系、形态变化与运动规律；利用图形描述、分析数学问题；建立形与数的联系，构建数学问题的直观模型，探索解决问题的思路。

直观想象在数学学习中起到连接现实与抽象世界的桥梁作用。学生善用直观想象，能轻松地将代数式具象为图形，深化理解；亦能将图形转化为代数式，简化难题，这一能力对于解决数学问题至关重要。随着教学观念的转变，数学教师愈发重视提升学生的直观想象素养。为提升学生的直观想象素养，笔者基于长期的教学实践，总结提炼了一些有效策略。

一、创设问题情境，启发几何直观思维

创设问题情境是建构主义教学理论的核心内涵之一。好的问题情境能激发学生学习的主动性，启发学生的思维。在高中数学教学中，教师可创设问题情境，引导学生深入分析问题并联想几何直观知识，构建个人解题思路和策略。这一过程促进了知识的融合，启发了学生的几何直观思维，提升了学生的知识迁移能力、类比能力和分析能力。

［例1］过点[（0，-2）]与圆[x2+y2-4x-1=0]相切的两条直线的夹角为[α]，则[sinα=]（ ）。

教师先引导学生在直观图形（如图1）中定位两条切线的夹角位置，为此需在直角坐标系中明确圆心、半径及相关点的位置，以便精确识别切线。接着，设置以下问题，引导学生深入思考。

问题1：找到角[α]后，我们应在何种结构中求解其三角函数？

问题2：当直线与圆相切时，具有何种性质？（圆心与切点的连线垂直于切线）

问题3：连接[BC]，[AC]后，虽知[BC⊥PB]，[AC⊥PA]（如图2），但角[α]不在一个明显的三角形内，所以需构造一个与直角关系相关且包含角[α]的三角形，以便构建等式。连接哪条线能达到此目的？

通过思考，学生认识到应连接[PC]。这样，在[Rt△PAC]中，不仅有垂直关系，还使得角[α]被等分（如图3），便于利用半角公式求解。

教师通过设计环环相扣的问题，引导学生结合图形进行问题的描述与分析，从而直观地把握数学问题的核心关系；利用直角三角形中的三角函数，建立等式中各变量之间的联系，并结合半角公式求解。由此可见，创设问题情境，并引导学生借助几何知识直观描述与分析问题，能有效提升学生的直观想象素养。

二、融合几何直观与变式教学，培养直观想象素养

复旦大学顾泠沅教授对变式教学进行了定义，强调其通过变换数学对象的非本质特征以及调整数学问题的呈现方式，从多个角度和方面来探讨问题，同时确保数学问题的本质特征始终不变。在高中数学教学中，教师在讲完某个知识点或者某道母题后，可改变问题的条件或者难度，设计变式练习。这样既能帮助学生巩固知识，又能引导学生从不同角度思考，从而培养学生的逻辑推理能力和直观想象素养。

以下是一个有关高三综合复习题的教学案例，该案例充分融合了几何直观和变式教学。

［例2］已知函数[g（x）=-xln（x+1）]，求[g（x）]的单调区间和极值。

减”的原则，可知[g（x）]在[（-1 ， 0）]上单调递增，在（0，+∞）上单调递减。[g（x）]的极大值为[g（0）=0]。

引导学生总结判断函数单调性的步骤：1.复杂函数的单调性需借助导函数判断，原则为“导函数看正负，原函数看增减”。2.若是导函数大于（或小于）零可解型，则可直接求解函数的增减区间。3.若是导函数含参数型，则应进行分类讨论，可先讨论导函数符号恒定的参数范围。4.若导函数为复杂函数，可通过二阶导数分析原函数的单调性或者逐一分析一阶导数组成部分的单调性，再结合特殊点的导函数值，确定导函数的符号。

以下是针对步骤4设计的难度提升的变式练习，能进一步提升学生的直观想象素养和综合应用能力。

［变式］已知函数[f（x）=-x+lnx]，若[f（x）≤xex-2x-m]恒成立，求实数[m]的取值范围。

“变式”中运用的解题思维与例2相同，但在求解导函数的零点时结合特殊值却没有那么容易得到导函数的零点，而是需要借助一个抽象零点[x0]，去找原函数的增减区间，再结合特定的计算技巧求解。

完成变式教学后，教师应引导学生总结规律：对于复杂函数，无论是求极值、最值，还是寻找零点、确定参数范围，关键都是深入分析并确定函数的单调性。

三、运用数形结合，搭建数与形的桥梁，提升学生的直观想象素养

数形结合融合了直观与抽象、感知与想象，教师应引导学生在直角坐标系中结合图形，体验采用代数方法解决几何问题的便捷，同时在几何直观中融入代数运算，领略几何中的数学之美，以此改变学生对数学的刻板印象。在此过程中，数量关系通过图形性质得以直观化、形象化甚至简化，从而更便于解决问题。因此，教师在教学中运用数形结合搭建数与形的桥梁，对提升学生的直观想象素养至关重要。以下以2022年高考数学北京卷第10题为例进行教学实践说明。

A. [-5，3] B. [-3，5] C.[-6，4] D. [-4，6]

向量的数量积有两种主要计算方法：一是几何法，通过直观地在几何图形中确定向量及两向量夹角的余弦值来计算；二是代数法，在坐标系中通过向量的坐标来计算。

这两种方法都是将题目中的抽象描述具体化，利用向量数量积的知识，在几何直观中寻找解题的突破口，循序渐进地分析问题并最终解决问题。这一过程，学生的直观想象素养得到了提升，逻辑推理能力得到了增强，数学综合能力也获得了全面提高。

面对数学教育的新挑战，我们应积极响应《数学课标》的号召，将提升学生的直观想象素养作为教学的核心任务之一，并不断探索和实践有效的教学策略与方法。

［   参   考   文   献   ］

[1]  中华人民共和国教育部.普通高中数学课程标准：2017年版2020年修订[M].北京：人民教育出版社，2020.

[2]  史宁中，王尚志.普通高中数学课程标准（2017年版）解读[M].北京：高等教育出版社，2018.

[3]  蒋海燕.中学数学核心素养培养方略[M].济南：山东人民出版社，2017.