添加辅助线　一题多解法

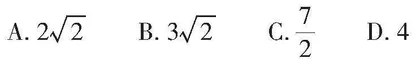
［摘 要］作辅助线是解决几何问题的关键手段，文章以一道有关三角形的题目为例，具体阐述如何通过巧妙添加辅助线，实现一题多解，进而拓宽学生的解题思路，提升他们的思维品质。

［关键词］辅助线；一题多解；初中数学

［中图分类号］    G633.6                ［文献标识码］    A                ［文章编号］    1674-6058（2024）32-0024-03

作辅助线是解决几何问题的关键手段。本文以一道有关三角形的题目为例，具体阐述如何通过巧妙添加辅助线，探索相关问题的多种解法，以拓宽学生的解题思维，提升学生的思维品质。

一、原题呈现

如图1，在[△ABC]中，[∠ACB=135°]，[CD⊥AB]，垂足为[D]，若[AD=6]，[BD=20]，则[CD]的长为（ ）。

这是一道以三角形为背景的几何题。题目图形由两个直角三角形拼合成一个钝角三角形，已知这两个直角三角形的各一边长及钝角的度数，要求出钝角三角形最长边上的高。解题的关键在于巧妙添加辅助线，构造出特殊的三角形，并利用特殊三角形的边角关系求解。

二、解法探究

解法1：如图2，作[△ABC]的外接圆，圆心为[O]，过点[O]作[OE⊥AB]于点[E]，过点[O]作[OF]∥[AB]，交[CD]的延长线于点[F]，连接[OA]，[OC]，[OB]。由垂径定理得[AE=BE]。因为[AD=6]，[BD=20]，所以[AB=26]，[AE=BE=13]，[DE=7]。因为[∠ACB=135°]，由圆内接四边形性质定理得弧[AB]所对的圆

评注：通过构造辅助圆，得到等腰直角三角形[AOB]，并作垂线[OF]分别构造矩形[OEDF]和Rt△[OFC]，借助矩形的性质实现边长的转换，及利用勾股定理求出[CF]的长。

评注：从135[°]的邻补角是45[°]入手，通过作垂线构造等腰直角三角形，并运用勾股定理求解各边的长。最后，利用“相似三角形对应边成比例”建立方程求[CD]的长。采用“算两次”策略，结合勾股定理与相似性质，成功求出[CD]的长。

解法3：如图4，过点[A]作[AE]∥[BC]，过点[B]作[BE]∥[AC]，[AE]，[BE]交于点[E]，过点[E]作[EF⊥BC]于点[F]，构造平行四边形[ACBE]，因此[AC=BE]，[AE=BC]。因为[∠ACB=135°]，所以[∠CBE=45°]，设[CD=x]，因为[CD⊥AB]，[AD=6]，

评注：本题是面积法在几何问题中的一个典型应用实例。通过作平行线构造平行四边形，再作垂线构造等腰直角三角形，利用平行四边形对角线分割面积相等的性质，得到面积等式[S△BCE=S△ABC]，据此建立方程，通过解方程求出[x]。

解法4：如图5，将[△ADC]沿[AC]翻折得到[△AEC]，将[△BCD]沿[BC]翻折得到[△BCF]，延长[AE]、[BF]交于点[G]，因为[CD⊥AB]，所以[△ADC]、[△AEC]、[△CDB]、[△CFB]均为直角三角形，因为[∠ACB=135°]，所以[∠ACB+∠ACE+∠BCF=270°]，所以[∠ECF=90°]，所以四边形[ECFG]是矩形，所以[∠G=90°]，因为[CE=CF=CD]，所以四边形[ECFG]是正方形，设[CD=x]，则[EG=FG=x]，因为[AD=6]，[BD=20]，所以[AE=6]，[BF=20]，所以[AG=x+6]，[BG=x+20]，在Rt[△AGB]中，由勾股定理[得AB2=AG2+BG2]，即[262=（x+6）2+（x+20）2]，解得[x=4]或[x=-30]（舍去），所以[CD=4]，故选D。

评注：当[x=4]时，[△ABG]的三边恰好是勾股数5、12、13的两倍，即10、24、26，此解法不仅基于扎实的基础知识与技能，而且超越基础层面，展现了命题者对学生思维的训练，很是巧妙。

评注：由135[°]的邻补角是45[°]入手，构造“一线三等角”的K型图，利用[△FEA ]≌[△ADC]，推导出[△FEB ]∽[△CDB]及其各边的代数关系。最后，通过相似三角形对应成比例建立方程求解，实现了全等三角形与相似三角形的综合运用。

得[x=4]或[x=-30]（舍去），所以[CD=4]，故选D。

评注：由135[°]角入手，构造“一线三等角”的K型图。与解法5相比，本解法构造的三个等角是三个钝角，而解法5构造的是三个直角。本解法主要利用等腰直角三角形与矩形的性质，为相似三角形的对应边提供数据支持，最后通过相似三角形对应边成比例建立方程求解。

评注：通过构造两个等腰直角三角形[△ADM]与[△BDN]，进而构造出相似三角形[△AMC]与[△CNB]。利用相似三角形对应边成比例建立方程求解。之所以要构造等腰直角三角形，是因为图形中有[∠ACB=135°]，135[°]与45[°]互补，这一角度关系为构造相似三角形提供了关键条件。

解法8：如图9，在[AD]上截取[DE=CD]，连接[CE]，因为[CD⊥AB]，所以[△CED]是等腰直角三角形，所以[∠CED=45°]，所以[∠A+∠ACE=45°]，因

评注：本解法构图比较简单，只构造了一个等腰直角三角形，然后利用“母子型”相似三角形[△AEC ]∽[△ACB]，根据对应边成比例建立方程求解。

评注：本解法通过在左右两个方向上构造两个等腰直角三角形，得到两个135[°]的钝角三角形，与已知[∠ACB=135°]相等。通过导角得到另一组等角，从而确立相似三角形[△ACE]与[△CBF]。最后，利用相似三角形对应边成比例建立方程求解。

综上，解题时作辅助线，应以启发思考为突破口，以突出通性通法为抓手，以培养学生学习能力为宗旨，引导学生学会学习并逐步提高思维水平，进而提升学生的数学核心素养。