经历算法建构，感悟运算一致性

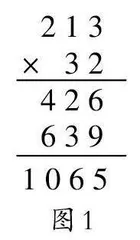
［摘 要］以苏教版数学教材四年级下册“三位数乘两位数的笔算”的教学为例，通过解读运算一致性，设计以下的教学活动：复习旧知，帮助学生回忆两位数乘两位数的算法；自主探究，促使学生发现三位数乘两位数的算法；延伸拓展，引导学生发现多位数乘多位数的算法；融入史料，帮助学生了解中外不同的算法。这样教学，有利于引导学生经历算法建构的过程，理解乘法笔算的算理，感悟运算一致性，提升他们的数学素养和问题解决能力。

［关键词］苏教版；算理；算法；运算一致性

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）18-0012-03

《义务教育数学课程标准（2022年版）》强调，在数与运算的教学中，通过整数的运算，感悟整数的性质；通过整数、小数、分数的运算，进一步感悟计数单位在运算中的作用，感悟运算的一致性。加减法运算的一致性体现为：相同计数单位上的数字相加减，计数单位不变；乘除法运算的一致性体现为：计数单位与计数单位相乘除，计数单位上的数字与计数单位上的数字相乘除。

在教学苏教版数学教材四年级下册“三位数乘两位数的笔算”时，教师先引导学生复习两位数乘两位数的算法，再组织学生探究三位数乘两位数的算理和算法，最后延伸拓展到四位数乘两位数、四位数乘三位数的乘法，使学生感悟运算一致性，获得核心素养的提升。

一、解读运算一致性

运算一致性是指在进行数学运算时，遵循统一的运算规则和运算顺序，使得运算结果符合数学逻辑的一种运算策略。运算一致性的核心在于相同计数单位个数的累加或递减。无论是整数、小数还是分数，运算都可以看作是计数单位的累加或递减。加法是所有运算的基础，表示相同计数单位的累加；减法则是加法的逆运算，表示相同计数单位的递减。乘法和除法也可以看作是加法与减法的扩展，乘法是求相同加数的和，而除法则是乘法的逆运算。

运算一致性分为加减法运算一致性、乘法运算一致性、除法运算一致性等，其中，乘法运算一致性又分为整数乘法运算一致性、分数乘法运算一致性、小数乘法运算一致性。

整数乘法运算一致性主要表现在运用乘法运算律进行整数乘法运算。如25×3=20×3+5×3=（2×3）×（10×1）+（5×3）×（1×1）=75。首先，将25从计数单位的角度进行分解，并根据乘法对加法的分配律进行拆解；其次，将每一个数都基于计数单位进行分解，利用加法和乘法的交换律与结合律，将计数单位上的数字与计数单位上的数字相乘、计数单位与计数单位相乘，得到一个新的数字与一个新的计数单位；再次，将新的计数单位与新的数字相乘，得到部分积；最后，将两个部分积相加，即可得到最终的运算结果。可见，整数乘法需要进行两类运算：一是将计数单位与计数单位相乘（这两个计数单位可以相同，也可以不同），从而得到新的计数单位；二是计数单位上的数字与计数单位上的数字相乘，得到新的计数单位上的数字。

二、教学过程

1.复习旧知，回忆两位数乘两位数的算法

出示题目：月星小区有16幢楼，平均每幢楼住28户。月星小区一共住了多少户？

师：请算一算月星小区一共住了多少户。

生1：28×16，先用第二个乘数16中的6去乘第一个乘数28，等于168；再用第二个乘数16中的1去乘第一个乘数28，等于280；最后，把168和280加起来，等于448。

师：我们一起来看一下这个乘法竖式。当用第二个乘数16中的6去乘第一个乘数28等于168时，为什么168中的8要写在个位上？当用第二个乘数16中的1去乘第一个乘数28等于280时，280中的8为什么要写在十位上呢？

生2：因为第一步算6×28=168，这里表示168个一，所以168中的8要与个位对齐；第二步算10×28=280，这里表示28个十，所以280中的8要与十位对齐。

师：用个位上的数去乘，就得到几个一；用十位上的数去乘，就得到几个十。

【设计意图】乘法运算的学习是一个逐步深入和拓展的过程。考虑到部分学生可能在长时间的学习过程中遗忘了两位数乘两位数的算理和算法，课始通过复习两位数乘两位数的算法来快速唤醒学生的记忆，帮助学生重新理解乘法的本质和意义，为后续学习三位数乘两位数的算法打下坚实的基础。

2.自主探究，发现三位数乘两位数的算法

（1）探究三位数乘两位数的算理和算法

出示题目：月星小区有16幢楼，平均每幢楼住128户。月星小区一共住了多少户？

师：请算一算月星小区一共住了多少户。

生3：128×16，先用第二个乘数16中的6去乘第一个乘数128，等于768；再用第二个乘数16中的1去乘第一个乘数128，等于1280；最后，把768和1280加起来，等于2048。

师：这位同学说得非常清楚。我们来观察一下28×16和128×16这两个算式，它们有什么相同点和不同点？

生4：这两个算式的相同点是都用个位上的数去乘，就得到几个一；用十位上的数去乘，就得到几个十。在计算过程中，这两道乘法算式都计算了28×16……

生5：这两个算式的不同点是，28×16是两位数乘两位数，而128×16是三位数乘两位数……

生6：相同点是它们都是乘法竖式计算，计算方法是一样的。

【设计意图】这个环节，先将两位数乘两位数的算法与三位数乘两位数的算法有机地联系起来，以此引导学生探索三位数乘两位数的算理和算法。这样不仅可以锻炼学生的计算能力，还能培养他们的逻辑思维和问题解决能力。然后组织学生比较两位数乘两位数与三位数乘两位数的算法，使学生发现这两种乘法运算的相同点和不同点，加深对乘法运算本质的理解。

（2）完成三位数乘两位数的练习

师：同学们，三位数乘两位数的计算学会了吗？（出示题目：213×32，309×26）我们来练一练。

生7：213×32，先用第二个乘数32中的2去乘第一个乘数213，等于426；再用第二个乘数32中的3去乘第一个乘数213，等于6390；最后，将426和6390相加，等于6816。309×26，先用第二个乘数26中的6去乘第一个乘数309，等于1854；再用第二个乘数26中的2去乘第一个乘数309，等于6180；最后，将309和6180相加，等于8034。

师：（出示图1）刚才老师看到有一个同学是这样计算的，谁来说说他错在哪里？

生8：639的位置写错了，因为第二个乘数32十位上的3乘213，得到639个十，所以639中的9应该写在十位上。

【设计意图】精心设计“练一练”环节，挑选了两道具有代表性的题目，其中一题还涉及乘数中间有0的特殊情况。这样意在帮助学生形成正确的计算思路，逐渐掌握算法，巩固运算的基础知识，提高他们的计算能力和应对复杂情况的能力。同时，呈现、分析学生的错题，促使他们深入理解三位数乘两位数笔算的算理，在辨析中进一步掌握算法，逐步形成计算技能。

3.延伸拓展，探究多位数乘多位数的算法

师：同学们，我们已经掌握了三位数乘两位数的算法，那大家猜一猜什么时候学习四位数乘两位数的算法？（有的学生说在五年级上册学习，也有的学生说在五年级下册学习，还有的学生说在六年级上册学习……）

师：大家都猜错了！今天学习之后，都不用学习多位数的笔算乘法了，你们知道这是为什么吗？

生9：因为不管是三位数乘两位数，还是四位数乘两位数、五位数乘两位数……它们的计算方法都是相同的：先用第二个乘数个位上的数去乘第一个乘数，得到几个一；再用第二个乘数十位上的数去乘第一个乘数，得到几个十；最后，把这两个数加起来。

师：（出示4213×32）谁来说说四位数乘两位数是怎么计算的？

生10：先用第二个乘数32中的2去乘第一个乘数4213，等于8426；再用第二个乘数32中的3去乘第一个乘数4213，等于126390；最后，将8426和126390这两个数加起来，等于134816。

生11：我发现213×32和4213×32是有联系的，第一个加数是在原来426的前面加了8，第二个加数是在原来639的前面加了12。

师：你发现了四位数乘两位数与三位数乘两位数的联系，真是一个善于观察的孩子！（出示4213×132）谁来说一说四位数乘三位数又是怎么计算的？

生12：先用第二个乘数132中的2去乘第一个乘数4213，等于8426；再用第二个乘数132中的3去乘第一个乘数4213，等于126390；然后用第二个乘数132中的1去乘第一个乘数4213，等于421300；最后，将8426、126390和421300这三个数加起来，等于556116。

师：现在明白为什么五、六年级不再学习多位数乘法的原因了吧？

生13：多位数乘法的计算方法都是一样的，都是先用第二个乘数个位上的数去乘第一个乘数，得到几个一；再用第二个乘数十位上的数去乘第一个乘数，得到几个十；然后用第二个乘数百位上的数去乘第一个乘数，得到几个百；最后，把这几个数加起来就可以了。

【设计意图】这一环节先巧妙制造认知冲突，引发学生深度思考问题“那大家猜一猜什么时候学习四位数乘两位数的算法”，再告诉学生从此不再学习多位数的乘法了。这样教学，意在引起学生的好奇心和探究欲，促使他们深入思考多位数乘法之间的共同点，得出结论：无论是三位数乘两位数，还是四位数乘两位数，其计算方法都是相同的。即都是先用第二个乘数个位上的数去乘得到几个一，再用第二个乘数十位上的数去乘得到几个十，然后用第二个乘数百位上的数去乘得到几个百，最后把这几个数相加，得到最终的乘积。

4.融入史料，了解中外不同的算法

师：同学们，我们掌握了多位数乘法的计算方法，想不想看看古代欧洲是怎么计算乘法的？（出示古代欧洲的乘法计算竖式，见图2）你能看明白每个数是怎么来的吗？

生14：32是8×4得到的，280是70×4得到的，400是100×4得到的；160是8×20得到的，1400是70×20得到的，2000是100×20得到的；最后，把这六个数相加，结果是4272。

师：你觉得古代欧洲的乘法计算和我们这节课学习的乘法计算有什么相同点？

生15：都是用第二个乘数每一位上的数分别去乘第一个乘数，在竖式计算时都要相同数位对齐。

师：这节课，你有什么收获？

生16：学习了三位数乘两位数的计算方法。

……

【设计意图】教师通过历史文化元素，向学生介绍古代欧洲的乘法计算，让学生感受数学的悠久历史和丰富文化。同时，引导学生在比较中发现古代欧洲的乘法计算和这节课学习的乘法计算的相同点，使学生不仅习得新知，还感受到了数学文化的魅力。

三、教后反思

在小学数学中，“三位数乘两位数的笔算”这一内容不仅是竖式乘法的延伸，更是培养学生逻辑思维、问题解决能力和数学素养的关键。教学中，通过算理和算法的结合，引导学生经历算法建构的过程，感悟运算一致性，既能增强教学效果，又促进了学生核心素养的发展。

1.明确算理，培养竖式的逻辑思维

算理是数学运算背后的逻辑和原理。教学中，通过自主探究和小组交流活动，先引导学生掌握三位数乘两位数的竖式计算方法，再进一步引导学生理解无论是三位数乘两位数还是多位数乘法，都是计数单位与计数单位相乘，即计数单位上的数字与计数单位上的数字相乘，这就是运算一致性。同时，在竖式计算过程中，引导学生按照一定的顺序和步骤进行思考。如先确定乘数的位数，再用每一位上的数去乘另一个乘数，最后将得到的积相加。这种有逻辑、有条理的思维方式，不仅能提高学生的解题效率，还有效锻炼了他们的逻辑思维能力。

2.掌握算法，形成正确计算的技能

算法是数学运算的具体操作步骤。本课教学重点引导学生探索竖式乘法的计算方法，并让学生寻找出错的原因，以帮助学生熟练掌握这一算法，逐渐形成计算技能。

总之，基于运算一致性，在乘法计算教学中，教师要帮助学生理解乘法笔算的算理和算法，不断巩固和提高他们的计算技能，培养他们的数学素养和问题解决能力，促进学生全面发展。

［ 参 考 文 献 ］

[1] 李芳芳.找准基点：让“一致性”学习成为可能：以“数与运算”教学为例[J].小学数学教育，2024（6）：9-10.

[2] 陈光明.重构数与运算一致性  形成结构化知识体系[J].辽宁教育，2024（7）：27-30.

（责编 杜 华）