借助“教—学—评”一致性，落实核心素养

［摘 要］以苏教版数学教材四年级下册“三角形的内角和”的教学为例，解读教材后设计以下的教学活动：借助三角尺，引导学生明确三角形的内角和；提出猜想，引导学生验证三角形的内角和；应用结论，引导学生计算三角形的未知角；总结归纳，引导学生畅谈学习心得体会。这样，基于“教—学—评”一致性进行教学，能有效落实核心素养，促进学生全面发展。

［关键词］苏教版；内角和；“教—学—评”一致性

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）18-0015-03

《义务教育数学课程标准（2022年版）》（以下简称“数学新课标”）细化了评价与考试命题建议，“注重实现‘教—学—评’一致性，增加了教学、评价案例，不仅明确了‘为什么教’‘教什么’‘教到什么程度’，而且强化了‘怎么教’的具体指导，做到好用、管用”。“教—学—评”一致性是指教师的教、学生的学、课堂评价是一致的，都是围绕教学目标展开的。教师要依据数学新课标、教材和学情来制订教学目标，力求明确、具体、可观察和可测量，不仅能反映学生的学习结果和层次，还能为教学过程和教学评价的设计提供依据。

教学苏教版数学教材四年级下册“三角形的内角和”时，我们通过研读数学新课标，深入分析教材和学情，制订了以下的教学目标：（1）能准确标出三角形的内角，知道直角三角形、等边三角形的内角和；（2）初步提出三角形内角和的猜想，通过算一算、量一量、拼一拼等操作活动，验证出所有三角形的内角和是180°。

一、解读教学内容

“三角形的内角和”一课对应的核心素养是推理意识，具体表现是知道可以从一些事实和命题出发，依据规则推出其他的命题或结论；能够通过简单的归纳或类比，猜想或发现一些初步的结论；能对自己及他人的问题解决过程给出合理解释。本节课的学段目标是帮助学生形成初步的推理意识；内容要求是引导学生探索并知道三角形的内角和是180°；学业要求是通过对图形的操作探究，感知三角形的内角和是180°，能根据已知两个角的度数求出第三个角的度数；学业质量是能认识常见的三角形，形成空间观念、量感和几何直观；教学提示是可以从特殊的三角形入手，通过直观操作，引导学生探究得出三角形内角和的度数，增强几何直观。

因此，我们确定了本节课教学的核心目标是引导学生经历一系列的猜想、验证和应用活动，根据三角形的特征，发现三角形的内角和为180°，形成推理意识。同时，我们对这节课的核心目标进一步具体化：一是分析，学生能具体指出三角形的三个内角，并知道内角和怎么求；二是猜想，学生能根据特殊的三角形，发现三角形的内角和是180°，并提出自己的猜想；三是验证，学生能够分清条件和结论，列举出更多的三角形例子，在验证中得出结论；四是讲理，学生能够清晰地表达猜想和验证的过程，说明三角形的内角和是180°。

本节课安排了三个学习任务：第一个任务是出示一副三角尺和一个等边三角形，帮助学生明确三角形有三个内角，并知道如何计算三角形的内角和，意在引导学生关注这些特殊的三角形的三个内角和是180°；第二个任务是引导学生根据特殊的三角形提出猜想“所有三角形的内角和是180°”，并为学生提供若干个形状和大小各不相同的三角形，让学生通过量一量、折一折、算一算等方法验证三角形的内角和；第三个任务是让学生说一说自己验证猜想的过程和得出的结论，并回顾整节课的学习，谈谈自己的收获。

二、教学实践

1.借助三角尺，明确三角形的内角和

师：（出示一副三角尺和一个等边三角形）同学们，这是我们熟悉的三角尺，你们对三角尺有哪些了解？

生1：我知道三角形有3个顶点，3个角和3条边。

生2：我知道第一块三角尺有一个90°的直角和两个45°的锐角，第二块三角尺有一个90°的直角和两个分别是30°与60°的锐角；等边三角形的每个角都是60°，它们都是锐角。

师：同学们，请仔细观察这3个三角形，它们有什么共同点？

生3：这3个三角形中都有2个锐角。

生4：我发现不同的三角形的三个角加起来都是180°。比如说，第一块三角尺的三个内角和是90°+45°+45°=180°，第二块三角尺的三个内角和是90°+30°+60°=180°，等边三角形的内角和是60°+60°+60°=180°。

师：在数学上，我们把三角形三个内角度数的和，叫作三角形的内角和。这节课，我们就来研究三角形的内角和。

【设计意图】由于学生对三角尺上每个角的度数都比较熟悉，而且在先前的学习中已经探索并计算过每块三角尺的三个内角和为180°，为进一步探索与发现三角形的内角和奠定了基础。课堂上，通过问题培养学生主动探索和发现问题的意识，激发他们的好奇心和求知欲，使他们不再被动地接受知识，而是主动地寻找问题的答案。

2.提出猜想，验证三角形的内角和

（1）量出三角形的内角并计算内角和

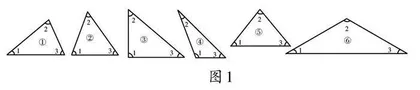
师：刚才我们发现这3个三角形的内角和都是180°，那是不是其他三角形的内角和也是180°呢？老师为大家准备了一些三角形（见图1），现在我们就来验证三角形的内角和。想一想选择哪些三角形来验证，并说明自己选择的理由。

生5：我会选择①、③、④号这3个三角形来验证，因为①号是锐角三角形，③号是直角三角形，④号是钝角三角形。

生6：我会选择①、③、④、⑤号这4个三角形来验证，因为①号是锐角三角形，③号是直角三角形、等腰三角形，④号是钝角三角形，⑤号是等边三角形。

生7：我会测量出所有三角形三个角的度数，验证每个三角形的内角和。我觉得验证三角形的数量越多，就越能包括所有的情况。

师：大家都有了自己的选择，接下来请测量出你选择的三角形的内角度数，并计算出三角形的内角和，记录在表格中。

生8：我测量出①号三角形的内角分别是40°、70°、70°，即内角和是180°；②号三角形的内角分别是70°、55°、55°，即内角和是180°；③号三角形的内角分别是90°、50°、40°，即内角和是180°；④号三角形的内角分别是110°、30°、40°，即内角和是180°；⑤号三角形的内角分别是50°、80°、50°，即内角和是180°；⑥号三角形的内角分别是30°、120°、30°，即内角和是180°。

【设计意图】通过测量内角度数的活动，学生不仅发现三角形的内角和为180°这一知识点，还学会如何运用所学知识解决实际问题。

（2）拼出一个平角并发现内角和

师：如果不用量角器量出三角形中每个角的度数，你还有其他方法证明三角形的内角和是180°吗？

生9：可以想办法把一个三角形中的3个角拼在一起，如果这3个角能拼成一个平角，就说明三角形的内角和是180°。

师：现在请你拼一拼三角形的三个内角，如果需要工具就上台领取。

生10：我先把一个三角形的3个角分别剪下来，再把这3个角拼在一起，发现正好能拼成一个平角，所以三角形的内角和是180°。

生11：我发现把一个三角形上面的角往下折，左边的角往右折，右边的角往左折，这三个角正好拼成一个平角，所以三角形的内角和是180°。

生12：我将3个完全一样大小的三角形的三个角拼在一起，发现正好是一个平角，所以三角形的内角和是180°。

……

【设计意图】通过“如果不用量角器量出三角形中每个角的度数，你还有其他方法证明三角形的内角和是180°吗？”这个任务，激发学生的探究兴趣和好奇心，使他们不断尝试、调整，最终成功地将三角形的三个内角拼成了一个平角。

3.应用结论，计算三角形的未知角

师：（出示图2）我们通过不同的方法验证了三角形的内角和是180°，现在就运用这个结论来计算出每个三角形中未知角的度数。

生13：第一个三角形，已知两个角分别是40°和60°，因为三角形的内角和是180°，所以这个三角形中未知角的度数是180°-（40°+60°）=80°；第二个三角形，已知两个角分别是110°和55°，因为三角形的内角和是180°，所以这个三角形中未知角的度数是180°-（110°+55°）=15°；第三个三角形，已知两个角分别是90°和55°，因为三角形的内角和是180°，所以这个三角形中未知角的度数是180°-（90°+55°）=35°。

生14：第三个三角形，我有补充。因为这是一个直角三角形，其中一个锐角是55°，所以这个三角形中未知角的度数是90°-55°=35°。

师：（出示图3）请同学们用一张正方形纸折一折，并填一填。

生15：第一个图形是正方形，正方形可以分成两个三角形，因为一个三角形的内角和是180°，所以一个正方形的内角和是180°×2=360°；第二个图形是三角形，内角和是180°；第三个图形也是三角形，内角和是180°。

【设计意图】上述教学，安排了两道练习题。第一题要求利用“三角形内角和等于180°”的结论来计算三角形中未知角的度数，意在深化学生对所学知识的理解，培养他们灵活运用所学知识解决问题的能力。第二题要求将一张正方形纸沿对角线对折，并填写对折后图形的名称与内角和的度数，意在加深学生对三角形内角和等于180°的认识，帮助学生积累图形变换的经验。

4.总结归纳，畅谈学习心得体会

师：回顾这节课，我们经历了怎样的学习过程？

生16：一开始，我们选择三角尺和等边三角形这些特殊的三角形进行探究，后来选择尽可能多的三角形来验证三角形的内角和。

生17：我们用量出三角形的三个内角的度数和将三角形的三个内角拼成一个平角这两个方法，验证了三角形的内角和是180°。

生18：我们用“三角形的内角和是180°”这个结论，计算出三角形中未知角的度数。

师：通过这节课的学习，你有哪些收获？

生19：我知道了三角形的内角和是180°，由此可以推算出正方形的内角和是360°。

生20：我学会了可以根据特殊的现象进行猜想，并通过举例验证自己的猜想。

师：数学是一门讲道理的学科，通过猜想、验证、应用等过程，可以帮助我们理越辩越明。

【设计意图】以问题为引，鼓励学生畅谈学习心得体会，意在帮助学生回顾整个学习过程，思考在这一过程中的体验、感受以及所取得的进步，从而培养他们的反思能力和自主学习能力。

三、教后反思

教学“三角形的内角和”这节课后，我们深感这不仅仅是三角形内角和知识点的传授，更是对学生数学核心素养的一次全面培养。

1.目标统领下实现“教—学—评”一致性

在本节课教学中，我们明确设定了教学目标，即让学生掌握三角形内角和的知识点，并能够运用所学知识解决实际问题。通过课后的作业和测试，我们发现大部分学生都能说出三角形内角和的推导过程，并能正确计算出三角形的内角和，这说明有效达成了教学目标。

2.核心素养下实现推理能力的培养

课始，给学生提供特殊的三角形，引发学生提出“所有三角形的内角和是180°”的猜想；课中，在验证三角形内角和的过程中，鼓励学生通过量、折、算等方式进行推理验证。这样不仅能加深学生对三角形内角和的理解，培养他们的逻辑推理能力，还有助于学生在推理过程中逐渐形成严谨的思维习惯，这对他们未来的学习和生活都具有重要意义。

当前，“教—学—评”一致性的理念逐渐成为教学实践的核心。数学课堂中，教师应基于“教—学—评”一致性，通过明确的教学目标设定、有序的教学内容组织以及灵活多样的教学评价方式，有效培养学生的数学核心素养。

［ 参 考 文 献 ］

[1] 谢翔翔，王琦.靶向单元作业，促“教—学—评”一致：以“扇形统计图”为例[J].小学教学参考，2023（17）：16-21.

[2] 章莉.指向教学评一致的数学试题命制[J].小学数学教育，2024（Z2）：37-38，75.

（责编 杜 华）