“模态分析”课程中信号处理案例教学探究

［摘 要］ 振动信号处理是模态中的关键步骤，针对现有“模态分析”课程中对信号处理重视不够的问题，通过引入案例式教学法，以振动信号处理在模态分析中的应用为背景，生动地展示离散傅里叶变换、快速傅里叶变换和短时傅里叶变换等多种信号处理方法的区别和联系，引导学生由浅入深地理解傅里叶变换的基本原理、变换目的和工程应用，激发学生的学习兴趣，提高教学质量。采用仿真的微电机转子的不平衡信号，验证了FFT能够有效消除转子系统的模态对振动信号的影响，并提取出不平衡信号的幅值和相位。

［关键词］ 模态分析；信号处理；傅里叶变换；不平衡信号提取；案例教学

［基金项目］ 2017年度国家自然科学基金项目“编织复合材料不确定性分布式参数识别方法研究”（11602112）；2023年度国家自然科学基金项目“基于等几何分析的高空长航时飞行器气动弹性耦合建模与颤振预示”（52202445）；2020年度江苏省高校自然科学基金“非线性动力学模型修正的灵敏度分析方法研究”（20KJB460003）

［作者简介］ 姜 东（1985—），男，湖北天门人，博士，南京林业大学机械电子工程学院副教授，硕士生导师（通信作者），主要从事机械振动研究；张梅升（2000—），男，安徽桐城人，学士，南京林业大学机械电子工程学院2022级机械工程专业硕士研究生，研究方向为转子动力学；杭晓晨（1990—），男，江苏苏州人，博士，南京林业大学机械电子工程学院讲师，硕士生导师，主要从事机械结构动力学与控制研究。

［中图分类号］ G642.0 ［文献标识码］ A ［文章编号］ 1674-9324（2024）23-0109-04 ［收稿日期］ 2023-07-19

模态分析作为振动特性分析的基础，对于振动工程领域具有重要的意义。模态分析建立在实测信号的基础上，一般采用加速度传感器对结构的振动响应进行实时监测，并将监测得到的信号数据输入计算机中进行处理，对结构系统进行频率响应分析以及模态识别是模态分析的主要任务［1-3］。

振动信号是结构物在不同激励下的振动响应数据，由于结构物受到动态载荷的响应会产生复杂的振动信号，同时易受到环境噪声的干扰，因此需要对振动信号进行进一步处理，以提取出信号中的重要特征。信号处理是从感知到的信号中提取有用信息以及去除无用信息的过程，其目的是帮助人们更好地理解和分析信号［4］。在模态识别中，通常需要先对采集到的振动信号进行处理，如滤波去噪和特征提取等操作，以得到更精确的振动信号；再将处理后的振动信号应用于频率响应分析中，来获取结构物在不同激励下不同振型的振动特性。通过分析和处理这些振动信号，可以识别出结构物的不同模态，并进一步获得结构物的固有频率、阻尼比等信息［5］。

在处理实测到的振动响应数据时，常用的信号处理方法有时域分析、频域分析、时频分析等。在教学中，学生对时域分析掌握得比较好，但是对频域分析和时频分析方法普遍表示难以理解［6］。对此，笔者在教学中引入案例教学法，对几种傅里叶变换的基本原理、实际应用和案例分析进行有针对性的教学，引导大家积极思考，由浅入深地理解每种信号变换的区别和联系、优势和缺点，进而掌握模态分析中常用的振动信号处理方法［7-8］。

一、原理简介

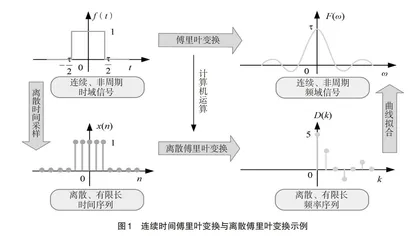
时域中的振动信号通过傅里叶变换可转化为频域中随频率变化的信息，在实际应用中，计算机只能处理离散信号，所以对信号f（t）进行时域采样，得到离散样本x（n），对它进行傅里叶变换得到的X（ω）中的频率自变量ω是连续变化的，需要对ω进行离散化采样，得到离散化的频谱，最终建立起离散时间变量n和离散频率变量之间的映射关系，这是离散傅里叶变换（Discrete Fourier Transform， DFT）。

计算机中常用的快速傅里叶变换（Fast Fourier Transform， FFT）是一种DFT的快速算法。为了计算变换后的每一个值需要进行N次复数乘法运算，计算x（n）的N点DFT总共需要N2次复数乘法和N（N-1）次复数加法。当N较大时，DFT的运算量较大。通过逐次分解，可以把较长点数的DFT分解成较短点数的DFT，进而得到FFT算法。这种分解既可以在时域进行，也可以在频域进行。FFT的运算量远小于DFT，N越大，FFT的运算效率越高。DFT是FFT的基本理论，FFT是DFT的一种实用优化。

二、案例式教学实例

（一）门函数的变换

连续时间傅里叶变换和离散时间傅里叶变换均能进行频谱分析。在实际应用中，信号可能是模拟的连续信号，也可能是离散的序列。为了利用计算机或数字信号处理器来处理信号，需要将连续信号变成离散的序列，其频谱亦是如此。离散时间傅里叶变换将离散的序列变换为频率谱函数，它的频谱是连续的，不便于数字化处理；而DFT把离散的序列变换成离散的频谱，则可以通过计算机运算。

以宽度为τ，高度为1的门函数为例，它的时域图和傅里叶变换如图1所示。易知F（0）=τ，它在时域和频域都是连续、非周期的。为了在计算机中处理信号，需要对门函数进行离散时间采样，将连续、非周期的时域信号变成离散、有限长的时间序列，然后对时间序列x（n）进行DFT，如图1所示。将每个采样点对应的x（n）值进行DFT，可得到频率序列，其中D（0）=5，可以看到它的频率是离散的。最后，将离散的频率序列点通过曲线拟合得到频谱曲线，即可将离散、有限长的频率序列还原成连续、非周期的频域信号。

（二）FFT频谱分析

FFT是DFT的简化算法，不仅大幅提高了信号处理的运算速度，而且对于信号的频率识别上也有很好的敏感性，同时还能够较好地抑制由谐波、噪声造成的波形畸变和频率漂移。通过FFT，可以将时域信号转换为频率谱形式，进而对振动信号做频域分析［9］。在频谱图中，可以获得一些时域中看不到的信息，不仅可以看到各频率分量的大小，而且可以根据各频率信号的振幅关系获得信号能量在频域上的分布情况。然而，FFT是一种全局的变换，时域信号经过傅里叶变换后，就变成了频域信号，从频域是无法看到时域信息的。如图2（a）所示，对一段0～100 Hz线性递增的扫频信号进行FFT，从频谱图中，只能得到信号含有的频率成分，不能得知每种频率出现的先后顺序和具体时间。对此，需要应用时频分析的方法处理这类信号。

（三）时频分析

在实际环境中，大多数信号是非平稳的［10］。此时应用FFT分析机器产生的振动信号有较大局限性，它不能描述振动信号的频率内容随时间变化的情况，可通过短时傅里叶变换（Short Time Fourier Transform， STFT）对振动信号做时频分析。对0～100 Hz线性递增的扫频信号进行STFT，如图2（b）所示。从时频图中可以看到，该扫频信号的频率随时间的变化是一条斜线，不仅可以看到频率变化的范围是0～100 Hz，而且可以得知信号的频率是随时间线性递增的。显然，时频分析相较于FFT在处理非平稳信号时具有优势。

STFT的窗口长度对时频信息的分辨率有着重要的影响。窗口长度越小，时间上的分界线越清晰，即时间信息越清晰，但是频率信息变得模糊；窗口长度越大，频率谱越细，各频率成分显示得越清晰，但是时间信息变得模糊。综上所述，STFT中时间窗口较短可以提供更精细的时间分辨率，但是频率分辨率相对较差。时间窗口较长可以提高频率分辨率，但是会使时间分辨率降低，这使得STFT的时间分辨率和频率分辨率难以同时提高。

（四）不平衡振动信号提取

FFT在旋转机械的动平衡技术中有着重要的应用，不平衡信号特征结合影响系数法，可以求得不平衡转子等效到校正面上的不平衡量［11］。在提取的转子振动信号中，除了不平衡量引起的在工频的不平衡振动，转子系统的模态等对信号影响较大，通过FFT可以从振动信号中精确提取不平衡信号的幅值和相位［12］。

通过仿真算例来说明FFT在不平衡振动信号处理中的应用。一个微电机转子在动平衡测试时的振动信号主要包括其本身不平衡质量在工作转速2 100转/分钟（35 Hz）下产生的不平衡信号，支撑架的固有模态频率为27 Hz，转子与支撑架构成的整个系统第一阶模态频率为23 Hz，干扰频率为41Hz，以及白噪声和直流分量等其他信号，实验室环境下白噪声较小。基于以上分析，对微电机转子在动平衡测试时的振动信号采用如下表达式进行模拟：

在仿真算例中，转子在工频下的振幅A0=7μm，支撑架在固有频率下的振幅A1=1.5μm，系统在固有频率下的振幅A2=0.8μm，干扰频率下的振幅A3=0.4μm，相位均为0，添加高斯噪声，采样频率为500 Hz，得到转子振动信号的数据并进行不平衡信号提取分析。

应用FFT对微电机转子的不平衡信号提取效果进行分析。转子的实际振动信号和理想不平衡信号及其频域图如图3所示。由图3可知，FFT方法提取微电机转子不平衡信号时，对其他干扰信号频率的截断效果很好，能够有效地提取出转子不平衡信号的幅值和相位，进而可以确定转子不平衡量的大小和位置。

结语

“模态分析”课程中的振动信号处理案例教学，可以更好地将理论知识与实践应用相结合。学生需要深入理解各种信号处理的原理和特点，并探究出适合于不同应用场合的解决方案。通过FFT在处理微电机转子不平衡振动信号中的应用，引导学生将信号处理的理论知识用于解决振动工程实践中的实际问题。这种综合思考和实践操作能够加深学生对振动信号处理技术的理解。在教学中，教师需要根据实际应用精心设计案例的内容和情境，引导学生探究振动信号的处理方法，并激发其学习兴趣，增强课堂教学的吸引力。在模态分析的信号处理课程中引入案例式教学，是提高学生实践能力和教学质量的有效手段。

参考文献

［1］王伟，梅雄，张心羽，等.研究生机械动力学教学科研相结合的探讨［J］.实验科学与技术，2016（14）：6-10+30．

［2］何倩鸿，王科盛，杨平.可视化模态实验课程的开发与实践［J］.实验科学与技术，2015（13）：22-25．

［3］沈春根，盛雪德，陈寒松，等.机械动力学结构模态分析实验的教学改革［J］.实验科学与技术，2010（8）：106-108.

［4］张辛，王旱祥，董祥伟，等.振动系统各阶固有频率及模态测试探究性实验设计［J］.教育教学论坛，2019（11）：269-270．

［5］蒋培，何鑫垒，李天赐.可视化模态实验课程的开发与实践［J］.实验科学与技术，2022（25）：132-136．

［6］王荣.机械振动与模态分析课程体系改革与探索［J］.黑龙江教育（高教研究与评估），2012（1）：31-32．

［7］吴绍维.研究生振动结构模态分析课程教学改革与实践探究［J］.教育教学论坛，2020（18）：228-229．

［8］张铁军.研究生模态分析实验课中实施创新性教学的实践与思考［J］.东北农业大学学报（社会科学版），2005（1）：98-99．

［9］刘永春，赵艳影.一种悬臂梁模态测试方法［J］.力学与实践，2019（41）：571-578．

［10］王秀芳，高丙坤，姜春雷，等．《模态分解算法与应用》案例教学探索［J］.教育现代化，2020（7）：107-109．

［11］黄峰.刚性转子现场动平衡技术分析［J］.装备维修技术，2019（2）：157-158+114.

［12］耿慧.转子动不平衡信号幅相特征的精确提取方法［J］.铁道技术监督，2004（7）：44-45.

Exploration of Signal Processing Case Teaching in Modal Analysis Course

JIANG Dong， ZHANG Mei-sheng， HANG Xiao-chen， CHEN Wei-yu

（School of Mechanical and Electronic Engineering， Nanjing Forestry University， Nanjing， Jiangsu 210037， China）