“最优控制与状态估计”教学改革与实践

［摘 要］ 针对“最优控制与状态估计”课程的特点及以往教学过程中存在的问题，从融入思政元素、突出工程背景、激发学生工程实践能力等方面进行了探讨。在思政元素融入方面，从思想政治素质教学案例设计、科学素养教学案例设计两方面进行；在教学内容优化方面，从工程教学案例设计和引入工程软件两方面开展；在分阶段多元化考核方式改革方面，凸显了不同教学阶段的考核方式和考核重点。改革实践提升了思想政治教育的教学效果，培养了学生的创新思维与实践能力，为学生全面提升分析问题和解决问题的综合科研能力奠定了良好的基础。

［关键词］ 最优控制与状态估计；思政元素；多元化考核；实践能力培养

［基金项目］ 2021年度南京理工大学研究生课程建设项目“Optimal Control and State Estimation课程建设”（S110B018）

［作者简介］ 单 梁（1979—），男，江苏南通人，博士，南京理工大学自动化学院副教授，主要从事非线性系统的控制与应用研究；李 军（1970—），男，黑龙江哈尔滨人，博士，南京理工大学自动化学院教授，主要从事非线性系统的控制与应用、伺服系统控制研究。

［中图分类号］ G642.0 ［文献标识码］ A ［文章编号］ 1674-9324（2024）35-0061-04 ［收稿日期］ 2023-09-14

引言

2020年7月13日，习近平总书记就研究生教育工作做出重要指示，中国特色社会主义进入新时代，即将在决胜全面建成小康社会、决战脱贫攻坚的基础上迈向建设社会主义现代化国家新征程，党和国家事业发展迫切需要培养造就大批德才兼备的高层次人才［1］。对于研究生培养而言，重在“研究”二字，要使研究生具有创新思维方式，善于提问和思考，能够应用掌握的学科知识解决实际工程问题。

“最优控制与状态估计”课程是控制科学与工程学术型硕士和控制工程专业型硕士的一门学位课程。该课程作为现代控制理论的重要组成部分，是相关后续课程学习的基础专业课程［2-3］。“最优控制与状态估计”课程主要包括优化理论基础、经典变分法、极小值原理、动态规划、状态估计等内容。

如何保证学生在掌握教学大纲涵盖知识的基础上，对最优控制学科有一个整体的认知，并能够进一步利用所学知识点去解决实际工程问题，是“最优控制与状态估计”研究生课程建设的核心。

目前，课程教学过程存在如下问题：一是在原有教学计划中，课程思政教育目标不明确，教学案例未进行深入挖掘，不能体现出对学生世界观、人生观、价值观和方法论等深层次的教育作用。二是随着近几年专业型硕士招生规模的不断扩大，课程授课群体中学术型硕士的比例已远低于专业型硕士。专业型硕士的培养重点是提升工程实践能力。目前，教学内容数学化氛围浓厚，与实际工程背景存在一定的脱节，易造成学生课程学习后只知道求解题目，而不知道如何将最优控制理论和方法应用到实际工程中的现象。三是教学形式和考核方法略显单一。如何利用这几年大量涌现的网课资源，充分调动学生的自主学习能力，实施多元化的考核方式，是“最优控制与状态估计”课程教学改革中亟须解决的问题。

结合2022年南京理工大学研究生培养方案修订工作，对“最优控制与状态估计”课程的教学内容、教学方法、考核方式等进行了分析研讨，并逐步进行了改革试点。本文将从融入思政元素、突出工程背景和改变考核方式三个方面，阐述本次教学改革的主要工作。

一、课程思政案例设计

2019年3月，习近平总书记在学校思想政治理论课教师座谈会上发表重要讲话，提出“六要”，即政治要强、情怀要深、思维要新、视野要广、自律要严、人格要正［4］。课程思政建设是要寓价值观引导于知识传授和能力培养之中，帮助学生塑造正确的世界观、人生观、价值观，把立德树人作为教育的根本任务的一种综合教育理念［5］。

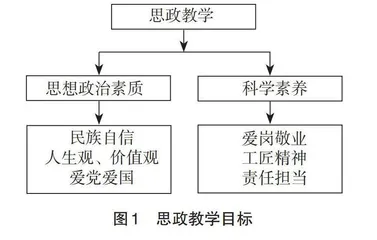
“最优控制与状态估计”课程是控制理论与控制工程学术型硕士和控制工程专业硕士的公共专业必修课程，每年授课人数超过130人。任课教师团队积极响应国家课程思政教育改革理念，持续探索将思政引入专业课程的教学，努力将专业课程与思政相融合，在教授理论知识的同时，加强对研究生思想政治素质和科学素养的综合培养，实现专业育人与育才的统一。总体教学目标如图1所示。

（一）思想政治素质教学案例设计

思想政治素质主要是指大学生的政治方向，培养其具备正确的政治观、人生观和价值观。在教学过程中，引入我国在控制领域的成就，潜移默化地激发学生的民族自豪感和自信心。

在第一章《优化理论的简介》中，引入都江堰水利工程的案例。公元前256年，李冰父子修建了都江堰水利工程，利用岷江上游的水资源灌溉川西平原。两千多年来，都江堰一直发挥着防洪和航运的巨大效益，是中国古代人民智慧的结晶，在世界水利史上写下了光辉的一页。都江堰工程体现出中国人很早就利用了优化控制思想，其设计巧妙体现了中国人民的伟大创造精神。

在介绍最优控制理论时，引入工程控制论学科开创者——钱学森的故事。钱学森于1954年所著的《工程控制论》（Engineering Cybernetics）直接促进了最优控制理论的发展和形成［6］。1955年10月8日，被美国政府非法软禁了5年的钱学森，冲破艰难险阻，终于回到祖国的怀抱。在空气动力学的研究中，钱学森针对空气阻力与速度线性相关及呈二次关系的两种特殊情况给出最优控制。以钱学森为代表的老一辈科学家勇攀高峰、拼搏实干的创新精神，为广大青年学生树立了榜样，培育了青年学生正确的世界观、人生观和价值观，为落实立德树人根本任务提供了丰厚滋养。

在讲授能量最优问题时，引入中国载人航天工程的案例。航空航天技术是高度综合的现代科学技术，也是一个国家科技水平的重要标志。航天器在太空飞行过程中，须寻找能量最优的运行方式。北京时间2022年11月4日15时12分，神舟十四号航天员乘组顺利进入中国天宫空间站梦天实验舱，以此激发学生的爱国主义热情与民族自豪感。

（二）科学素养教学案例设计

科学素养教学案例旨在培养大学生运用科学方法的能力，使其掌握科学思维和科学思想，在科学实践中做到实事求是，在职业生涯中做到爱岗敬业、守正创新。

在讲授无约束优化方法时，介绍提出各种优化算法的科学家生平：毕达哥拉斯（前580至前570之间—约前500），古希腊数学家，提出黄金分割概念。芝诺（约前336—前264），古希腊数学家、哲学家，提出了二分法。莱昂纳多·斐波那契（约1170—约1240），意大利数学家，提出斐波那契数。艾萨克·牛顿（1643—1727），英国物理学家、数学家，提出牛顿插值法。

列出众多科学家对一维搜索问题的研究历史，借此启示学生，学术研究需要刻苦钻研、一丝不苟的精神。

在讲授卡尔曼滤波知识时，引入流行病学预测模型的应用。基于现代控制理论中的状态预测、状态滤波理论的最优预测方法具有坚实的理论基础，大大提高了疫情预测的准确度和可靠性，最终形成解决疫情问题的思路和方法［7］。通过上述内容的讲授，激发、增强学生的社会责任感和社会担当，引导新时代青年学子以实现民族复兴和国家富强为己任。

二、突出工程背景，优化教学内容

“最优控制与状态估计”课程的主要特点是理论性强、内容丰富、数学推理多、公式多、计算繁杂。随着近几年专业型硕士招生规模的不断扩大，南京理工大学“最优控制与状态估计”授课学生中学术型硕士比例远低于专业型硕士。专业型硕士的培养重点是提升其工程实践能力，因此，本课程培养方案在修改时从增加工程案例、引入工程软件等方面优化了教学内容，加强了相关工程背景介绍。

（一）工程案例设计

在课程培养方案修订时，要求教师尽量在引入教学内容前，以具体的工程问题为切入点，师生一起探索该问题的解决方法，自然地引入教学内容。

1.讲述具有末端约束条件的最优控制问题时，引入导弹对地面移动目标攻击时的轨迹规划问题。为了实现在规定时间内攻击移动目标，提高毁伤效果和命中精度，这一有终端约束要求的轨迹规划问题可以转化为终端约束条件的最优控制问题。

2.讲述能量最优问题时，引入航天器姿态控制案例。航天器进行角度姿态控制时，系统除了完成从初始姿态到终端姿态的精确控制以外，还需要能耗量最小，因此，该姿态控制问题可转化为能量最优控制问题。

3.讲述极小值原理时，引入电动汽车能量管理系统案例。电动汽车以后驱电机和集成式起动发电机（ISG）的输出力矩为控制变量，以整车燃油消耗最小为目标的能量管理目标。该能量管理控制策略可以使用极小值原理设计。

4.讲述离散动态规划时，引入列车节能优化案例。为降低城市轨道交通的牵引能耗，需要以列车位置为自变量、牵引力/制动力的系数为控制变量构建列车节能速度曲线优化模型。因此，可以根据线路条件将位置进行离散化，把速度曲线优化问题转换为离散动态规划问题。

5.讲述卡尔曼滤波算法时，引入MEMS陀螺仪漂移补偿案例。MEMS陀螺具有体积小、价格低廉的特点，在消费类电子产品中广泛用于姿态定位控制，有效实现了隧道、停车场等场景中对GPS和电子罗盘信号的补充。但是MEMS陀螺的随机漂移问题难以避免，该问题可以使用卡尔曼滤波算法进行漂移补偿。

飞行器运行轨迹控制、工业过程控制、经济系统控制等案例的引入，能够让学生更好地理解最优控制理论的应用背景和实际意义。

（二）引入工程软件

在介绍非约束优化问题中的一维搜索方法时，由于该部分内容较为简单，因此，在教学中引入工程软件MATLAB，增加动手实践内容，以提高学生的实践能力和解决问题的能力。

1.布置无约束优化算法的分组仿真作业。对上课学生进行分组，每组分配2～3个单峰目标函数，要求采用2种以上的优化算法完成仿真实验，并对各种搜索算法的执行效率进行对比分析。仿真作业的动手操作，能够让学生深入理解如何应用理论算法解决实际工程问题。

2.设置研讨课分享优秀仿真案例。鼓励学有余力的小组或个人，对优化算法进行进阶研究。通过阅读新的学术文献，编写改进算法来提高搜索的效率和搜索精度。教师批改各组提交的作业后，挑选2组优秀作业在研讨课上进行分享。优秀案例分享能够充分调动学生学习的积极性，同时让学生在实际操作中深入理解无约束优化问题。

三、分阶段多元化考核方式

要检验学生是否掌握了“最优控制与状态估计”课程知识，是否能够应用所学知识解决一个实际的优化问题，原有单一的开卷考核方式难以全面评价学生的学习成效。因此，在本次培养计划调整中，课题组采用了分阶段、多元化的考核方式。多元化的课程考核可以更全面地评价学生的学习成果，有助于增强学生的学习兴趣和积极性，提高教学质量［8-9］。

（一）分阶段考核方式

在教学内容安排上，主要分为优化理论、最优控制和状态估计三个部分。根据授课重点的不同，针对每个阶段设定不同的考核方式。

优化理论部分：以仿真作业考核为主，开卷笔试考核为辅，课堂研讨为加分项。重点考核学生应用无约束优化和线性规划方法解决实际问题的能力。

最优控制部分：以开卷笔试考核为主，重点考核变分法、最小值原理在连续系统和离散系统中的应用。

状态估计部分：开卷考试和仿真作业考核并重，重点考核卡尔曼滤波器在连续系统和离散系统中的应用。

（二）多元化考核方式

由于每个教学部分考核的侧重点不一样，因此，对学生成绩的最终评定是综合了多种考核方式的结果。

学生成绩的分配比例为：开卷考试60%、仿真作业32%、课堂研讨8%。开卷考试按考卷成绩每人单独评分，仿真作业按照3人小组每组单独评分，课堂研讨按照小组自愿的原则报名单独评分。未参加课堂研讨的，总成绩最高以92分计。