智慧课堂在乡村初中数学教学中的实践及其反思

摘    要：基于智慧课堂进行教学设计，能给学生营造出更直观完善的课堂体验，增加学生实际操作经验，让学生成为课堂的主体。在实施教学前，教师需要明晰教材内容，并根据课标相关要求和学情确定教学重难点，然后进行有针对性的设计。在课前预习阶段，教师可以通过“智慧课堂”平台发布具有知识性和趣味性的学习资料，并了解学生的预习情况。在课中探究阶段，教师需要注重学生输出，借助数字化技术设置多个动态的、生成的学生自主探究环节以及讨论式的小组探究环节，并及时反馈学生探究中的疑问。在课后巩固阶段，教师可通过“智慧课堂”平台提供差异化的作业等，以帮助学生查缺补漏，及时调整自己的学习策略。

关键词：智慧课堂；乡村初中；数学教学

《义务教育数学课程标准（2022年版）》（以下简称“《义教数学课标》”）强调：“注重信息技术与数学教学的融合，改进教学方式，促进学生学习方式转变。”教师不仅应教会学生知识，更应成为学生自主探索并获取知识的引导者。乡村初中由于地域条件、学校软硬件和师资等方面的限制，在传统教学中处于弱势。而数字化背景下的智慧课堂可以打破时间和空间的限制，通过数字化工具将复杂抽象的知识直观、生动地展示出来，提高学生的学习兴趣和课堂参与度，使学习更加轻松快乐、有趣易懂、和谐高效。这就为乡村初中提升教学成效提供了契机。

所谓智慧课堂，指的是在现代化教育理念下，基于数字化的信息技术和教育软件，为教师获得更多教学资源、更好的创新及丰富的教学手段而提供平台和桥梁的一种教学模式。它可以运用于教学的各个阶段，包括课前预习、课中探究、课后巩固。基于智慧课堂进行教学设计，能给学生营造出更直观完善的课堂体验，增加学生实际操作经验，让学生成为课堂的主体。下面，笔者以沪科版义务教育教科书《数学》九年级上册第21章第2节《二次函数[y=ax2]的图象与性质》第1课时为例，具体介绍如何在乡村初中实施智慧课堂教学。

一、智慧课堂在乡村初中数学教学中的运用实践

打造智慧课堂，既能充分利用信息化在线教学的灵活性、反馈性、可重复性、可拓展性等优点，又能保持传统教学中师生互动、面对面知识精准传授、课堂氛围热烈等优势。《二次函数[y=ax2]的图象与性质》是学习一次函数的延续，是对函数内容的再认识，也是学生理解二次函数定义、建立二次函数模型的后续学习，具有承上启下的作用。基于智慧课堂对其实施教学时，需要根据课标相关要求和学情确定教学重难点，然后进行有针对性的设计。

（一）根据课标、学情确定教学重难点

《义教数学课标》对该节内容的要求是：通过对实际问题的分析，体会二次函数的意义，正确理解抛物线的有关概念；会用描点法画出二次函数[y=ax2]的图象，概括出图象的特点；掌握形如[y=ax2]的二次函数图象的性质，并能确定相应自变量的值，能解决相应的实际问题；通过动手操作、合作交流，积累数学活动经验，培养动手能力和观察能力。

这节课学生要面对曲线型函数图象，在用研究一次函数的方法研究二次函数时，出现了新的研究内容：对称性和最大（小）值。同时，分段讨论二次函数[y]随[x]的增大如何变化也是学生没有接触过的。虽然在研究一次函数时学生知道通过观察函数图象研究函数性质，但是仍然有许多学生不能很好地用图象来解释问题。

据此，笔者确定了这节课的教学重点和难点。

重点：从“数”（解析式）和“形”（图象）的角度理解二次函数[y=ax2（a≠0）]的性质，掌握二次函数解析式[y=ax2]与函数图象的内在关系。

难点：画二次函数[y=ax2（a≠0）]的图象，二次函数[y=ax2]蕴含的数形结合思想。

（二）基于智慧课堂的教学设计

在课前预习阶段，教师可通过“智慧课堂”平台发布具有知识性和趣味性的学习资料，吸引学生提前熟悉课程的相关概念和重难点，然后通过学生在平台上的留痕了解学生的预习情况，并灵活调整教学侧重点。在课中探究阶段，教师需要注重学生输出，借助数字化技术设置多个动态的、生成的学生自主探究环节以及讨论式的小组探究环节，并及时反馈学生探究中的疑问，如可借助电子白板等进行各种教学演示，借助视频、在线几何画板等让课堂“活”起来，通过实拍答题、投票、积分奖励等增强课堂的互动性，从而提升学生的课堂参与度和学习数学的热情。在课后巩固阶段，教师既可通过“智慧课堂”平台提供差异化的作业，以满足不同学习能力学生的学习需求，也可通过线上互动问答、批改上传作业、生成个性化的学习记录和错题集，帮助学生查缺补漏，及时调整自己的学习策略。

1.课前预习

课前教学准备：预习微课（前置学习）、“智慧课堂”平台线上备课、上课课件PPT制作、在线画板函数动态图象制作、课后讨论发布（画图动手作业）。

【前置微课预习】

操作1：提前2天在“智慧课堂”平台上布置预习微课，上传1节7分钟的“二次函数[y=ax2]的图象与性质”微课（让学生课前通过微课了解函数图象的基本研究过程和逻辑）。

操作2：课前通过“智慧课堂”平台检查学生的预习情况。

2.课中探究

【活动一】类比探究二次函数[y=ax2（a≠0）]的图象与性质

［导入］视频播放：探究一次函数图象与性质的过程。

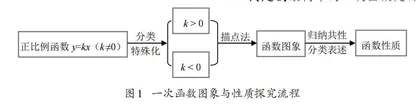
［环节1］梳理还原一次函数图象与性质探究的流程（如图1所示）。

设计意图：二次函数与一次函数虽然图象、性质特点不同，但研究方法都是从特殊到一般。复习一次函数的探究过程，引导学生自主梳理函数的研究方法和逻辑，可为学生后续自主探究并归纳出二次函数的图象和性质作准备。

问题1：最简单的二次函数是哪个？类比一次函数的探究，当a=1时，画出二次函数[y=x2]的图象。观察它的图象，你发现有哪些特征？

［环节2］教师在“智慧课堂”平台设置“随堂演练”——教学回馈，学生在线完成描点法画图并提交，教师在大屏上展示部分学生提交的成果，如：（1）列表（表略）；（2）在直角坐标系中描点；（3）用光滑的曲线连接各点，得到函数[y=x2]的图象（图略）。

追问1：用描点法画函数图象有哪几步？自变量x的取值范围是什么？

追问2：观察这个函数图象，它有什么特征？

设计意图：引导学生提炼归纳观察的方法，思考研究二次函数图象性质的几个图象特征，如对称性、最值、增减性等，尝试类比探究特殊的二次函数[y=x2]的图象和性质。

问题2：在同一直角坐标系中，请作出函数[y=12x2]，[y=2x2]的图象，对比两个图象，通过观察，你能发现它们有什么相同特征？有什么不同特征？归纳当a>0时，二次函数[y=ax2]的图象有什么特征？

［环节3］教师在“智慧课堂”平台设置“随堂演练”——实拍答题，学生在学案坐标系中完成作图后用平板拍照上传，大屏展示部分学生的作图结果。

追问1：这些函数图象有什么共同点？这种共同点与函数的什么因素有关？

追问2：这三个函数有什么不同的地方？是什么因素造成了这种差异？由此你可以得到什么结论？

生：a>0时，开口向上，a越大，开口越小。

设计意图：让学生通过动手实践，自主探究并归纳出二次函数[y=ax2（a>0）]的图象特征，体会数学学科从特殊到一般的探究方法过程，提升课堂参与度，培养学科兴趣。

［在线画板动态展示］希沃在线画板展示函数[y=x2]，[y=12x2]，[y=2x2]的描点连线成图过程（如图2所示）。

问题3：类比a>0时的研究过程，研究当a<0时，二次函数[y=ax2]有何图象特征？

［环节4］小组自主探究：（1）在同一直角坐标系中，画出函数[y=-x2]，[y=-12x2]，[y=-2x2]的图象，并观察这些抛物线有什么共同点和不同点；（2）当a<0时，二次函数[y=ax2]的图象有什么特点？

［师生活动］教师在“智慧课堂”平台设置“随堂演练”——实拍答题，每小组讨论后派一名代表上传本组作图和讨论结果，教师大屏展示各组提交的成果。

追问1：通过刚刚的探究，你能猜测[y=x2]与[y=-x2]的图象有什么关系吗？

追问2：你能总结出a>0和a<0时的图象特征吗？

［学生活动］列表，描点，连线得图象。得出结论：a决定抛物线的开口方向——a>0时，开口向上，a越大，开口越小；a<0时，开口向下，a越小，开口越小；|a|相等，抛物线的开口大小、形状相同，|a|越大，开口越小。

设计意图：让学生经历观察、猜想、发现、归纳、论证的过程，培养自主探究能力、观察能力、归纳能力、论证能力。而类比a>0时从特殊到一般的研究过程，观察函数图象的特征，进而归纳得到二次函数[y=ax2（a<0）]的图象与性质，还可以发展学生类比和数形结合的数学思想。

问题4：你能总结出[y=ax2]的图象和性质吗？

［生成预设］性质主要包括四个要素：开口方向、对称轴、顶点坐标、最值。

（1）a决定抛物线的开口方向和开口大小；

（2）顶点坐标为（0，0），对称轴是直线y=0（y轴）；

（3）抛物线[y=ax2]的最大值（最小值）为0。

设计意图：再次总结归纳，有条理地分类整合二次函数[y=ax2]（[a≠0]）的图象和性质，培养学生的表达能力、归纳能力。

［在线画板动态展示］希沃在线画板展示a的取值变化与二次函数[y=ax2（a≠0）]的图象关系，让学生直观感受。

【活动二】探究二次函数[y=ax2（a≠0）]的图象增减性

问题5：已知二次函数[y=5x2]，有两点（-4，y1），（-2，y2）在函数图象上，分组讨论有哪些方法可以判断y1、y2的大小关系？

方法1：可以画出草图，将两点在图象上标出，然后比较y的大小。

方法2：可以将x的值代入函数关系式，算出对应的y值，再进行比较。

方法3：可以利用增减性来比较，两点均位于对称轴左侧，y随x的增大而减小，所以y1>y2。

追问：若问题条件改成“已知二次函数[y=ax2]，有两点（-4，y1），（-2，y2）在函数图象上”，如何快速判断y1、y2的大小关系？

［生成预设］当a>0时，开口向上，距离对称轴越近y越小。

［环节5］归纳：请同学们对二次函数[y=ax2]（[a≠0]）的增减性作出小结。

［生成预设］二次函数的增减性。

（1）当a>0时，有两种情况：在对称轴左侧，y随x的增大而减小（即从左到右下降），符号语言为“当x1<x2<0时，y1>y2”；在对称轴右侧，y随x的增大而增大（即从左到右上升），符号语言为“当0<x1<x2时，y1<y2”。

（2）当a<0时，也有两种情况：在对称轴左侧，y随x的增大而增大；在对称轴右侧，y随x的增大而减小。

［在线画板动态展示］希沃在线画板展示二次函数[y=ax2]（[a≠0]）图象中y随x变化的增减性质，让学生直观感受。

［随堂检测］在平板上发放随堂检测答题卡，实时统计学生答题情况。

（1）抛物线[y=x2]与[y=-x2]的图象的关系是什么？

（2）二次函数[y=-x2]与[y=ax2]的图象如图3所示，那么a的值可以是（    ）