基于“理解数学、理解学生、理解教学”的单元整体教学探究

摘    要：单元整体教学是一项系统的工作，其设计需要基于联系以构建单元整体，基于学生以鼓励自主探究.在进行单元整体教学前，教师需要基于“理解数学、理解学生、理解教学”，综合分析单元内容、学情能力、单元整体框架，确定单元整体教学目标.具体教学中，教师可通过问题前测激发学习欲望，通过类比关联明确研究思路，通过有序探究培养学习能力，通过聚焦特例得出预备定理，通过回归一般渗透转化思想，通过总结梳理完善认知结构，帮助学生形成系统性和整体性的认知.

关键词：理解数学；理解学生；理解教学；单元整体教学；初中数学

当前，初中数学教学存在“思维浅显化、探究虚假化”“知识课时化、内容碎片化”等问题.前者的表现是，学生对一个结论，往往只知其然而不知其所以然.这是因为教师往往直接对照知识讲授，而不介绍其来龙去脉，使学生缺少大观念的引领，难以进行有序的思考活动.后者的表现是唯教材论，一节课只讲相应课时中规定的内容，对知识的整体性、前后联系性视而不见.这就导致知识内容呈现碎片化、分散式样态，数学思想方法的一致性和数学思维的连贯性被人为分割，使学生很难形成系统性和整体性的认知.

因此，教师需要在“理解数学、理解学生、理解教学”的基础上进行单元整体设计.“理解数学”即理解数学知识的结构体系，知道教什么；“理解学生”即理解学生的现有水平，知道怎么教；“理解教学”即理解教学方式，知道为什么这么教.基于“理解数学，理解学生，理解教学”进行单元整体设计，可以有效帮助学生整体、系统和深入地理解数学知识，发展数学核心素养.下面，笔者以浙教版义务教育教科书《数学》九级上册第4章《相似三角形》第4节《两个三角形相似的判定》为例，从单元整体视角出发重构教学设计，旨在增强学生对这一内容的整体认识，让探究自然且真实地发生.

一、单元整体教学设计思路

单元整体教学是一项系统的工作，教师需要把握以下设计思路.

（一）基于联系，构建单元整体

《义务教育数学课程标准（2022年版）》（以下简称“《义教数学课标》”）明确指出，数学知识的教学要注重知识的“生长点”与“延伸点”，把每堂课的数学知识置于整体知识的体系中，重视知识的结构和体系，处理好局部知识与整体知识的关系.这促使教学设计从关注单个知识点转向关注知识的整体性.单元整体教学设计不是简单的课时拼盘，它是将具有相同或类似结构的一类课进行关联思考并整体设计，有助于引领学生整体、系统、深入地研究问题，理解概念本质，掌握学习方法，发展学科核心素养.

（二）基于学生，鼓励自主探究

学生是学习的主人，要让学生在发现、提出、分析、解决问题的过程中，乐于动手，勤于参与.研究表明，当学生在学习过程中积极参与、自主探究时，其思维是最活跃的，其对知识的掌握也是最高效的.因此，构建以学生为主体、以教师为主导、以学生自主探究为主线的教学模式，有利于学生准确把握数学概念、掌握数学基本方法、提升数学学习能力，让学习成为一个生动活泼、富有个性的过程.

二、基于“理解数学、理解学生、理解教学”确定单元整体教学目标

在进行单元整体教学前，教师需要基于“理解数学、理解学生、理解教学”，综合分析单元内容、学情能力、单元整体框架，确定单元整体教学目标，保证教学设计的合理性［1］.

（一）“理解数学”下的单元内容分析

《相似三角形》一章包含相似三角形的定义、性质、判定和应用等.相似的逻辑起点是全等，学生在八年级的时候学习了三角形全等的定义、性质、判定和应用.笔者将《两个三角形相似的判定》一节的3个课时组成一个单元，在其教学中，充分运用类比思想，引导学生理解三角形全等是一种既保角又保距的图形变换，而三角形相似则是一种只要求保角的图形变换，因此相似可以看成是全等的一般化，是条件弱化的结果.因此，该单元的重点是类比全等的学习来学习相似，同时借助判定定理的证明，发展学生的符号语言，培养学生的推理能力.

（二）“理解学生”下的学情能力分析

在八年级的时候学生已经接触过三角形全等的证明，所以对相似三角形判定方法的证明有一定的经验基础.但是相似比全等更加一般化，需要学生具备更强的抽象思维能力.教师可引导学生先对特殊位置关系下的三角形进行研究，然后将任意位置的两个三角形转化到特殊位置关系，体现从特殊到一般的数学思想.而运用预备定理证明相应的判定方法，实际上是在培养学生的应用意识.因此，该单元的难点是让学生自然得出预备定理，然后运用预备定理对各个猜想进行证明.

（三）“理解教学”下的单元整体框架设计

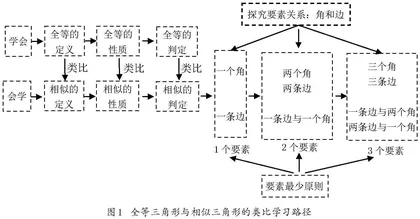
在该单元的学习过程中，自始至终坚持两条学习路径，即类比学习以及从特殊到一般再由一般转化成特殊的数学研究思路，让学生先学会，再会学［2］，充分发挥学生的主观能动性，让学生在真实探究中收获知识和能力.类比学习，即引导学生类比全等三角形的相关知识学习相似三角形，具体如图1所示.

（四）综合上述理解，确定单元整体教学目标

单元连接着课程与课时，单元目标是数学课程整体目标的具体化.《义教数学课标》对“图形的相似”作了如下要求：了解图形相似的意义；了解相似三角形的判定定理，会判断简单的相似三角形；理解相似三角形的性质定理.将上述课程目标具体化，结合基于“理解数学”“理解学生”“理解教学”的分析，可得到该单元的整体教学目标.

（1）知道从要素出发研究图形关系，形成研究几何图形关系的大观念.

（2）能将各种猜想按要素多少进行分类，从而有序探究，培养分类意识和规范意识.

（3）在探究相似三角形的判定定理时，掌握从特殊到一般，再将一般转化成特殊的研究方法，培养严谨的思维能力和推理能力，保证单元内容育人价值的有效落实.

三、基于“理解数学、理解学生、理解教学”的单元整体教学实践

（一）问题前测，激发学习欲望

上课伊始，教师可提出简单的问题，引导学生回顾相似三角形的定义，并使学生在解决问题的过程中感受到已学方法的烦琐，知道学习新方法的必要性，激发学习的内驱力.这样既能让所有学生迅速地进入状态，也能帮助教师了解学生对知识的掌握情况.

问题：如图2，在正方形网格中存在格点△ABC和△DEF，你能判定这两个三角形相似吗？

生：通过证明△ABC和△DEF三个角相等、三条边对应成比例，根据定义，可以判定两个三角形相似.

师：是的，从定义当中我们可以得到三角形相似的一种判定方法，但是这样的判定方法太烦琐，需要判定六个条件，那是否有更简洁的判定方法呢？图形相似关系的研究会让你们联系到以前学习过的哪类图形关系？

（二）类比关联，明确研究思路

相似的判定方法不应由教师直接给出，而要引导学生发现相似与全等的特殊关系.学生可以类比三角形全等的判定方法，迁移得到相似的判定方法.而在寻找相似的判定方法时，学生不太可能一下子就寻找到正确的判定方法，因此教师需引导学生如何进行有序研究.

师：全等可以看成是相似比为1的相似，全等是相似的特殊情况，所以在探究三角形相似的方法时可以类比三角形全等的探究过程.

［活动］教师与学生一起回顾全等的判定方法，引导学生明确可通过探究要素关系来研究图形关系，为研究三角形相似奠定方向.

（三）有序探究，培养学习能力

教师先让学生写出他们认为能判定两个三角形相似的猜想，然后与学生一起将这些猜想按要素多少进行分类，从一个要素到两个要素再到三个要素，让学生形成有序研究的意识.通过画出反例，可以说明结论不成立；但是画不出反例，不能说结论就一定成立，还需要推理证明，这样能培养学生思维的严谨性.

师：可以通过研究角和边的关系来判定两个三角形的关系，你会研究几个角、几条边？

生：条件越少越好，最好是两个三角形的一个角相等或者一条边成比例就可以判定相似.

师（提示并追问）：两个三角形中一条边成比例，无论在什么情况下都是成立的，因为比值并没有固定，所以一条边成比例对判断两个三角形相似没有任何价值.那么，一个角相等可以判定相似吗？

生：明显不可以.这两种情况都很容易画出反例（如图3所示）.

师（再次追问）：那接下来该如何研究呢？

生：一个要素不行，那就研究两个要素，包括两个角相等、两条边成比例、一个角相等和一条边成比例.

［活动］学生画图（如图4所示），自主探究，看看两个要素能否判定三角形相似.

学生发现，两条边对应成比例，以及一个角相等、一条边成比例（包含边是对边和邻边两种情况），都可以画出反例，这说明这样的两个三角形是不相似的，但是当三角形两个角相等时则画不出反例.画不出反例不代表就一定是相似的，那么要如何证明相似呢？

（四）聚焦特例，得出预备定理

在实际教学中，很多时候教师会直接给出基本图形，让学生证明然后得到预备定理，学生不知道为什么要铺垫预备定理，也不知道如何想到这个基本图形，这样就失去了探究的意义.因此，教师需要引导学生从特殊出发，给予学生脚手架，让学生的思维可以螺旋上升，这样的探究才是以学生为主的真实探究.

师：如何证明两个角对应相等的三角形相似呢？一般位置情况下的证明比较困难，我们可以怎么办？

生：我们可以先让两个角相等的三角形具有特殊位置情况，看看特殊情况下这两个三角形是否可以证明相似.

特殊位置1：在△ABC中，∠ADE =∠ABC，∠AED =∠ACB，且D，E分别是AB和AC的中点，DE为△ABC的中位线，判断△ABC和△ADE是否相似，并说明理由.

特殊位置2：在△ABC中，∠ADE =∠ABC，∠AED =∠ACB，D，E分别是AB和AC上的任意一点，DE为BC的平行线，判断△ABC和△ADE是否相似，并说明理由.

［活动］在教师的引导下，学生观察两个三角形的位置特点以及DE与BC的位置关系，得到判定三角形相似的预备定理.

（五）回归一般，渗透转化思想

有了预备定理的铺垫，学生知道当两个三角形具有特殊位置关系时是相似的，那么，一般位置关系的两个三角形，要如何证明它们相似呢？这就要渗透转化思想.

师：当△ABC和△DEF中有两个角相等，但是位置关系不特殊时，如何证明相似，你现在有想法了吗？

生：我们可以将不特殊的位置关系转化成特殊的位置关系.

师：如何将小三角形构造到大三角形中呢？

［活动］学生在AB，AC上分别找一个点E[ ′]，F[ ′]，使得△AE[ ′]F[ ′]≌△DEF，利用判定三角形相似的预备定理，可以得到△ABC∽△AE[ ′]F[ ′]，从而有△ABC∽△DEF，推出相似三角形的判定定理1“两个角对应相等的两个三角形相似”.

师（追问）：满足两个要素的三角形已经研究好了，那我们的研究是否结束了呢？

生：可以继续增加要素，看看是否还有其他判定方法.

［活动］学生对三个要素进行归纳，发现三个要素包括：①三个角相等；②两个角相等，一条边成比例；③一个角相等，两条边对应成比例；④三条边对应成比例.其中①和②与判定定理1是等价的，为表述简洁，将它们统一总结为判定定理1.学生对剩余的③和④进行探究，并画出相关图形（如图5所示）.

教学说明：对满足三个要素的两个三角形，即使是不成立的那种（一个角相等，角的邻边和对边成比例），学生也较难画出反例，那该如何证明呢？方法是一脉相承的，都是在大三角形中构造小三角形，将两个三角形转化到特殊位置上，然后运用前面得到的预备定理证明相似，从而得到判定三角形相似的定理2“一个角相等且角的两边对应成比例的两个三角形相似”以及定理3“三条边对应成比例的两个三角形相似”.