静态研究—动态研究—动静结合

摘    要：推理是数学思维的表现形式，也是科学态度和理性精神的基础.教师要认真研究课程标准对培养推理能力的要求，设计符合学生认知的情境问题，带领学生从“静态研究”“动态研究”“动静结合”三个层面进行探究.在具体教学中，教师需要引导学生从关注静态的知识和静态的结论中蕴含的图形运动变换规律，体会“静中有动”的层级，逐步上升到感悟几何直观，掌握“动中有静”的辩证关系，最终能够“动静结合”，实现静态数学观与动态数学观的融通，提升推理能力，发展核心素养.

关键词：静态研究；动态研究；动静结合；推理能力

《义务教育数学课程标准（2022年版）》（以下简称“《课程标准》”）指出：“在对图形性质的研究过程中，核心素养的感悟由感性上升为理性，要求在建立空间观念、几何直观的基础上，逐步形成推理能力.”推理能力有助于逐步养成重论据、合乎逻辑的思维习惯，形成实事求是的科学态度与理性精神.这就要求学生在学习图形相关知识时，能从“演绎证明”“运动变化”“量化分析”等角度探究图形的性质与关系.

在众多的数学问题研究案例中，几何问题往往格外受到青睐，主要原因是其不仅具有鲜明的个性、丰富的题型，还有如万花筒般的解题方法与过程.由此，几何问题成为思维训练的良好素材.经过长期的探索与实践，笔者认为，在几何图形教学中，引导学生从“静态研究”“动态研究”“动静结合”三个层面进行探究，可帮助学生理解问题的本质和原理，发展学生的推理能力.

一、“静态研究”：体会“静中有动”，强化演绎推理

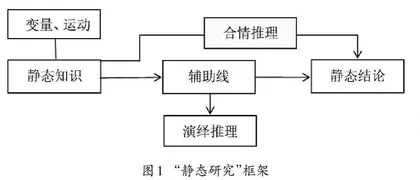
欧氏几何是世界上第一个相对成熟的演绎体系，历来都被作为培育推理能力的基本载体［1］.“静态研究”主要包括对构成原图形的相关要素，以及通过添加辅助线后构造的新图形进行再研究的过程（其框架如图1所示）.它是训练思维的基本方法，指向的是静态的知识和静态的结论.教师需要引导学生关注静态的知识和静态的结论中蕴含的图形运动变换规律，以体会“静中有动”.

例1：如图2，四边形纸片ABCD中，∠A＝∠C＝90°，BC=DC.若AB＋AD＝8，求该纸片的面积.设AD＝x（0 ≤ x＜8）， AB＝y（0 ≤ y＜8）.

笔者引导学生对例1的条件、图形、结论和问题等信息进行分析、处理，从而建构条件与结果之间的关联，通过添加辅助线将陌生的问题转化为熟悉的问题，在发展合情推理的同时，强化演绎推理.

（一）初步计算

问题1：若设x＝1，y＝7，你能计算该纸片的面积吗？

问题2：若x＝4，y＝4呢？若x＝0或y＝0呢？

引导学生体会变量x，y变化时，纸片的面积恒定.赋值分析是寻求命题结论的常用手段，通过不断地尝试，达成对命题结论的预判，从而为后续的推理论证提供方向.

（二）推理论证

下面呈现学生通过“静态研究”解决例1的思路.

思路1：过点C分别作CE⊥AD于点E、CF⊥AB于点F，将原四边形转化为正方形.

思路2：延长AB至点E，使BE＝AD（或延长AD至点E，使DE＝AB），将原四边形转化为等腰直角三角形.

推理能力主要是从一些事实和命题出发，依据规则推出其他命题或结论的能力.此环节的处理体现在以下三个方面：（1）对变量x，y进行赋值，使问题退化至某一“静止的时刻”，再通过定量计算求出纸片面积，发展学生的合情推理能力；（2）引导学生发现变量x，y变化时，原四边形的面积与变量取值无关，发展归纳推理能力；（3）四边形形状是变化的，而大小是确定的，故需要引导学生体会“静中有动”，通过添加辅助线，将变化的四边形转化为确定的正方形或等腰直角三角形的形状，强化演绎推理能力.

思考：若四边形ABCD的形状不确定，而面积确定，那么图2中蕴含着怎样的几何变换？

二、“动态研究”：掌握“动中有静”，感悟几何直观

前述研究中，“四边形的形状变化而大小确定”这一问题亟须深度研究，因此笔者采用“动态研究”（其框架如图3所示）的方式让学生感悟几何直观，掌握“动中有静”的辩证关系.几何直观主要指运用图表描述和分析的意识与习惯，可以把复杂的数学问题变得简明、形象，有助于学生探索问题解决的思路，预测结果，直观地理解数学，进而把握问题的本质，明晰思维的路径.在整个数学学习过程中，几何直观都发挥着重要作用.

“动态研究”强调“图形的变化”，即从运动变化的观点来研究图形，理解图形按着某种法则或者规律变成另一个图形的几何变换本质.几何变换具有动态性、直观性，它既是一种思想，也是一种方法，与欧氏几何的综合法最大的区别就是“动态”.在欧氏几何中，几何图形是静态的，而从几何变换的角度来看，图形则是动态的，不论是点、线，还是形，都是可以移动的.与欧氏几何的综合法相比，这其实是观念的变化［2］.

“动态研究”是基于动态视域的图形研究思路，运用纸片的分割或不分割，采用图形运动的方式把相同的边拼接，实现图形形状的变换，达成问题解决的目的.它是训练高层次数学思维的重要方法．

下面呈现学生通过“动态研究”解决例1的思路．

思路1：如图4，过点C折叠纸片，使点B落在AB上，沿折痕CE剪开纸片，将△BCE纸片和四边形ADCE纸片重新拼接，使CB与CD重合，得到新的“纸片”：四边形AECE′.

思路2：如图5，将△BCE纸片绕点C顺时针旋转90°至△CDE′；或如图6，将四边形AECD纸片绕点C逆时针旋转90°.

思路3：复制原四边形纸片3张，按图7的方式拼接得到大正方形（也可以从旋转的视角理解）.

思路4：两张同样的纸片拼接成直角梯形（图略）.

笔者引导学生运用“做”为支架的学习方式，利用KT泡沫板、打印纸、透明胶片、半透明纸片、“电子纸片”等作为实验操作的素材，既贴近学生现实，又符合学生的认知水平.“做”数学既能诠释知识的发生、形成、发展的过程，又能激发学生主动探究问题的兴趣［3］.

三、“动静结合”：理解“动静融通”，深化逻辑推理

在几何课程中，不仅几何概念、性质、关系是直观的，推理的方法也是直观的.几何直观在学习推理能力与证明时，往往是一把双刃剑：一方面，几何直观有助于明晰推理的方向与过程，降低推理的难度；另一方面，几何直观也可能会使学生无法感受到推理的必要性，从而导致学生用直观代替推理，或者缺少推理的合理步骤［4］.因此在教学中，教师既要掌握“静态研究”的严谨性，又要掌握“动态研究”的直观性，将二者密切结合，使学生在“静态研究”中体会“静中有动”，在“动态研究”中掌握“动中有静”，从而提升推理能力.

“动静结合”指运用几何变换的方式改变图形的结构后，再将新构图形中的动态因子、确定元素巧妙融合，进而运用数学核心知识解决问题的过程（其框架如图8所示）.“动静结合”是建立在理性的“静态研究”和动感的“动态研究”基础之上的，属于高阶的逻辑思维活动，能实现静态数学观与动态数学观的融通，使数学教学变得完整而有活力［5］.

例2：如图9，在矩形ABCD中，AB＝4，AD＝6，P，Q两点分别在AB，AD上，PB＝DQ，求CP＋BQ的最小值．

下面呈现学生通过“动静结合”解决例2的思路．

思路1：在透明纸上临摹△BCP得△B′C′P′，将△B′C′P′拼接到DQ上方，使点B′与点D、点P′与点Q重合.此时点B，C′均为确定点，根据“两点之间线段最短”可知，点Q运动过程中使点B，Q，C′共线即可.

思路2：连结DB，用透明纸临摹△BDQ得△B′D′Q′，将△B′D′Q′拼接到PB左侧，使点D′与点B、点Q′与点P重合.

思路3：用透明纸临摹四边形BCDQ得相等的四边形B′C′D′Q′，将四边形B′C′D′Q′拼接到PB左侧，使点D′与点B、点Q′与点P重合．

思路1遵循“图形变换、重组—寻求确定元素—抓住动态因子—定量计算”的探究过程，在“动静结合”的过程中实现了“动静融通”.在此过程中，学生既能掌握逻辑推理的基本形式，学会有逻辑地思考问题，又能在比较复杂的情境中把握事物之间的关联以及事物发展的脉络，形成重论据、有条理、合乎逻辑的思维品质和理性精神，增强交流能力［6］.（思路2、思路3与思路1的分析类似，不再赘述）

四、小结

推理是数学思维的表现形式，也是科学态度和理性精神的基础.《课程标准》和《普通高中数学课程标准（2017年版2020年修订）》对推理都有具体的要求，即从推理意识到推理能力再到逻辑推理素养，这既体现了核心素养发展的连续性，又体现了核心素养发展的阶段性和一致性.从“静态研究”到“动态研究”再到“动静结合”体现了次序性、进阶性、内隐性与外显性，显然与二者对推理的要求一致.

“动静结合”可解决“重结果，轻过程”“重思维，轻操作”“重论证，轻实证”的错误认知和矛盾体现，使数学的教与学趋向和谐、完整、统一，且富有美感，能让学生充分关注数学本质，理解数学原理，掌握数学知识，形成数学能力，发展数学核心素养.

参考文献：

［1］［4］［6］鲍建生，章建跃.数学核心素养在初中阶段的主要表现之五：推理能力［J］.中国数学教育，2022（19）：3-11.

［2］马波.中学数学解题研究［M］.北京：北京师范大学出版社，2011：122.

［3］李明树.纸片类数学实验教学的实践与思考［J］.中学数学月刊，2022（7）：47-49.

［5］喻平，董林伟，魏玉华.数学实验教学：静态数学观与动态数学观的融通［J］.数学教育学报，2015（1）：26-28.