连续开展课堂博弈论实验的效果分析

摘  要：从2019年到2022年，先后在东南大学交通学院15个不同班级开展连续多轮的博弈论实验，包括大二、大三和两个校区的研一学生。实验的基本原理是“最理性的决策是所有人选择0”，但在实际操作中多数人会做出不同的选择。统计结果表明，第1轮实验结果的平均值可以评估班级整体的思维能力和“理性程度”。在前2轮实验中，年龄越大的学生普遍结果越小，不同年份的班级结果差异很大程度上取决于生源质量，英语教学对实验结果几乎没有影响，但实验环境可能会影响结果，例如线上实验时学生可能会私下交流、产生“共谋”。另外，实验中出现一些有趣的现象，不同学生对于是否要进行第3或第4轮实验、是否要领取奖励、是否要采取“理性”的行为等话题有比较明显的分歧，值得进一步讨论。总而言之，连续多轮博弈论实验具有很好的教学互动效果，对不同背景的理工科学生群体均适用。可以有针对性地进行知识拓展，从而充分促进学生对博弈、人性、“理性”等概念的理解和认识。

关键词：博弈论；课堂实验；理性；人性；实验环境

中图分类号：G640      文献标志码：A          文章编号：2096-000X（2024）28-0091-06

Abstract： From 2019 to 2022， we conducted multiple rounds of game theory experiments in 15 different classes at the School of Transportation， Southeast University. The participating students included second and third-year undergraduates， as well as first-year graduate students from two different campuses. The mechanism of this experiment was "the most rational decision is that everyone chooses 0". But in practice， most people make different choices. The statistical results showed that the average results of the first round could be used to evaluate the overall thinking ability and "rationality" of the entire class. In the first two rounds， older students tended to have smaller results. The differences in results between different classes were largely influenced by the ability of the students' background. The use of English in teaching had almost no influence on the experimental results， but the experimental environment could affect the results. For example， in the online experiments， students may communicate privately and "collude". Additionally， some interesting phenomena emerged during the experiments， including the differences in opinions among students regarding whether to participate in the third or fourth round， whether to accept rewards， and whether to adopt "rational" behavior. These needs to be further discussed. In a word， conducting multiple rounds of game theory experiments is an effective teaching tool with strong interactivity. It is applicable to diverse groups of STEM students. By tailoring the knowledge expansion to meet the specific needs of each class， the students' understanding and awareness of many concepts can be significantly enhanced， including games， human behavior and "rationality".

Keywords： game theory; classroom experiment; rationality; human nature; experimental environment

博弈论是一门研究决策者在竞争和合作情境中行为的科学，被广泛应用于经济学、社会学、心理学和生物学等多个领域，对于理解各种社会现象的演化具有重要的价值[1]。正因为此，我国高校中很多专业在不同的课程中都开展了博弈论知识的教学。由于博弈论的公式和符号非常抽象，近年来很多学者开始引入博弈论实验的手段。这些有趣的实验[2-4]很多都适合在教室里进行，有助于改善教学效果和活跃课堂气氛，非常值得推广。

虽然国内很多学者已经开展了相关的教学研究[5-15]，但也存在着诸多局限性。虽然他们都对博弈论实验的互动效果给予了非常高的评价，但对博弈论实验的具体过程、具体统计结果，以及在实验中发生的各种现象缺乏进一步的分析和论述，也没有针对学生的反应和感受做更深入的挖掘。例如李军军等[5]、乔磊[6]、李攀艺等[7]并未给出博弈论实验的开展过程。李太龙[8]、马洪云[9]、李宾[10]、王选飞[11]描述了实验内容和开展过程，房琳等[12]介绍了开展实验后学生对具体知识点的掌握程度变化，支援[13]介绍了开展实验后学生成绩的提升效果，但均未给出具体的实验结果和细节。只有刘晓丽[14]、王新辉等[15]少数学者针对实验结果进行了定量的讨论和解释，具有更强的参考借鉴意义。

值得一提的是，虽然存在着多种可行的博弈论实验，但这些文献[14-15]所研究的博弈论实验内容基本相同，这个实验非常适合在课堂教学中开展。但在过去的实践中，基本上都只进行一次实验便结束，内容过于简单，对博弈论原理的诠释和挖掘还不够深入。事实上在一学期的连续多周课程里，完全有条件开展连续多次的重复课堂实验，从而进一步强化学习效果。因此，本文针对这一点进行了改进，并且在连续4年多个班级的教学中加以实践，发现了一系列有趣的现象，将在下文中予以详细介绍与讨论。

一  实验过程和原理

本文设计的实验题目如下。

“在0～100之间选择一个数字，当所有数字收上来之后，计算它们的平均数。数字最接近所有人平均数2/3的学生是赢家，会得到10元钱奖励。你会如何选择？”

另外，还有几条附加如下。

如果数字不在0～100之间，则不予考虑。

数字可以不是整数。

在纸上除了姓名、学号、选择的数字外，还需要写上选择的理由。

如果有多个赢家，则每人都有奖励。

实验时间为15分钟左右。

这一实验的纳什均衡点为0或1，最理性的选择是0。如果所有人都选择0，则所有人都是赢家，都能获得奖励。这在前人研究中已有详细的讨论[14]，此处不再赘述。在实际操作过程中，为让学生充分理解博弈的含义和效果，本文作者采取了连续多次课堂实验的形式，每次实验的要求均完全相同。

第1节课做第1次实验。

第2节课先讲解上次实验的结果，并进行原理简介，然后进行第2次实验。

第3节课先讲解上次实验的结果，然后酌情考虑是否要进行第3次实验。

如果有第3次实验，则在第4节课进行总结。

在不同的教学情境下（例如网络教学或英语教学），开展实验的细节会略有不同，但总之基本流程不变。另外，通常第1次实验用时较长，部分学生会用满15分钟才提交结果。但在后续第2、第3次实验中，因为熟悉了流程，多数学生会在10分钟甚至5分钟内就提交。

二  实验结果分析

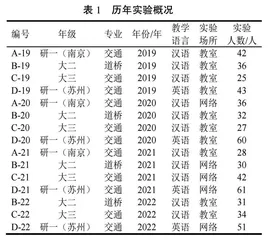
从2019年至2022年，本文作者先后在4个不同年龄段的班级内开展了多次实验，具体情况见表1。需要说明如下。

编号的字母和年级是一一对应关系。班级A和D是两组完全不同的研一学生，其中班级A的学生居住在东南大学九龙湖校区；班级D的学生居住在东南大学苏州校区，并且平时进行全英文教学。B是大二学生，C是大三学生。

为简便起见，下文均使用“字母-年份”来称呼某个班级。例如B-21表示2021年的大二班级。

此处从上到下的顺序代表做实验的时间顺序，例如A-19是2019年开展实验的第1个班级，D-22是2022年开展实验的第3个班级。

大三的交通专业全称为交通工程，研一的交通专业全称为交通运输规划与管理，但两者本质上是同一专业。

2022年的班级A因为课堂教学课时较少，最终没有做博弈论实验。

受疫情影响，有多门课程采用了网络教学方式，因此有多场实验在线上进行。不同教学形式对实验过程和结果的影响将在后文详细讨论。

因为偶尔有学生请假或旷课，所以每轮实验的参与人数有时略少于表格结果。

历年实验每一轮的统计结果见表2。概括地说，它们具有以下共性。

第1轮实验结果明显大于后2轮。这是因为在第2轮实验前，教师会对实验原理进行简要介绍，会提到“理论最优解是选择0”。这种介绍会对学生产生显著的影响，但在多数实验中，不会有很多人在第2轮选择0。

除个别班级（例如C-21）之外，多数班级在第1和第2轮的结果差别不大。例如第1轮结果普遍在12～23之间，第2轮结果普遍在4～10之间。虽然不同班级的学生特质不同，但他们对于实验的基本判断具有相似的倾向。

另一方面，不同班级的差异性也显而易见，在此分为4个角度进行讨论。

（一）  不同年级的对比

这种对比如图1所示，将每个年级实验的结果求平均值后发现，随着年龄的增长，平均值越来越低。换言之，年龄越大的学生越能考虑到较多的迭代次数，思维越深入。这种现象在第1轮和第2轮实验中定性一致。另外，C-21的第2轮实验结果非常特殊，将在第三章单独论述，此处图1（b）中大三年级的平均值未考虑C-21的结果。

（二）  不同年份的对比

通过对比发现，同一年级不同年份的结果存在一定差异，这来源于多种因素。此处以第1轮实验结果为例进行讨论。

1）大二的结果差异可能与学生来源有关。从图2（a）可以看到，2022年的结果最大。事实上因为大环境影响，全国范围内土木类专业在2022年的高考招生分数线显著下滑，这种专业选择上的偏好改变，也影响到了2022年秋季学期刚开学时大二学生“大类分流”的选择结果：最终进入道桥专业的学生的大一排名比以往更低一些。这可能影响了班级B-22在实验中的整体表现。