新工科视域下大学数学教学改革研究与实践

摘  要：该文剖释传统大学数学教育教学的缺陷，指出为适应社会飞速发展，在以学生为中心的思想指导下，从新工科视域角度，突出交叉融合，通过重塑教学理念、构建课程体系、优化教学模式等方面进行大学数学教育教学改革与实践。确立创新型卓越工科人才培养观，构建全贯通的大学数学课程体系，优化大学数学教学模式，竭力培养学生敏锐运用数学知识解决复杂工程问题的能力，培养学生积极主动的学习意识，提高课程教学质量，促使学生专业、素质全面发展。

关键词：新工科；大学数学；交叉融合；教学改革；课程体系

中图分类号：G642      文献标志码：A          文章编号：2096-000X（2023）02-0162-04

Abstract： The article explained the shortcomings of traditional mathematics teaching in the university， and proposed that in order to adapt to the rapid development of society， under the guidance of student-centered ideology， it is necessary to carry out the teaching reform and practice of college mathematics education from the perspective of new engineering， highlight the cross-integration， reshape the teaching concept， construct the curriculum system and optimize the teaching mode. And we need establish the concept of training innovative and outstanding engineering talents， build a comprehensive university mathematics curriculum system， optimize the university mathematics teaching model， strive to cultivate students' ability to use mathematics knowledge to solve complex engineering problems， cultivate students' active learning awareness， and improve the quality of course teaching and promote the comprehensive development of students' professional and quality.

Keywords： new engineering; University Mathematics; cross-integration; teaching reform; curriculum system

为培养适应新一轮科技革命和产业变革的卓越工程科技人才，我国于2017年先后推出“新工科”建设的“复旦共识”“天大行动”和“北京指南”，旨在建立中国工程教育的新范式[1]。2017年广西高校新工科研究与实践联盟成立，作为以理工科为主的院校桂林理工大学是发起高校之一，学校各专业纷纷开启了新工科建设与实践探究。而大学数学是各高等院校至关重要的公共基础课，是基础学科联络各专业学科的桥梁，学习质量对学生的后期发展发挥极其重要的支撑作用。新工科建设对大学数学教学提出了新要求，新工科建设强调以学为中心，突出能力培养。通过创新课程体系、教学模式等，从知识模块组合、强化数学实践等教学内容与教学方法改革，切实提高大学数学教学效果和人才培养成效。

大学数学教育教学，应当使学生掌握专业学习必需的数学知识，培养学生的逻辑思维能力，为工程技术人才培育和加强国家科技力量做出基础性的奉献。随着科学技术的急速发展，新工科建设对大学数学教学提出了新要求，要不断提高学生的数学实践创新能力，致力于培养学生灵活使用数学知识处理生产和生活中的实际问题，促进大学数学能够满足学生的专业应用需求，推动学生的专业良性发展。

一、传统大学数学教学模式中的问题

传统的大学数学教学模式单一且统一，教学理念陈旧，理论教学和实践教学不平衡、不协调，课程设置未考虑学生专业，缺乏学科交叉和过程交叉，导致学生将数学理论知识变更为解决问题的能力欠缺。但随着经济社会发展、产业结构转型和新工科建设的推进，传统的大学数学教学出现的问题日益凸显，主要如下。

（1）大学数学理论教学联络实际不足，教师工程实践经验短缺，工程实践有机融入数学教学不足。传统教学“以教师为中心”，侧重于数学理论知识传授，重视数学运算技巧，轻数学思想的倾向，忽略实践创新能力培养。忽略不同学生专业对数学的个性要求，忽视数学知识的实际运用和与专业知识的链接。课程与专业学科人才标准和规格要求缺少对接，导致教学效果、教学质量不能有效支撑不同专业培养人才的需要，以致大学生只是知识的消费者，而没有成为知识的开拓者，不利于培养学生的数学思想和实践创新能力。

（2）课程群设置单一，课程设置不凸显专业特色，数学实践课程不足。大学数学课程主要包括高等数学、线性代数和概率统计等课程，一般在大学的前三个学期完成课程的教学，课程设置没有根据专业需求而有所不同，致使数学学习与专业学习、专业能力发展之间的关联度较低。后期缺乏相应的数学实践课程，如数学实验、数学建模等课程，缺少数学实操实践活动的“做数学”过程，导致学生进行深化和数学运用能力、工程能力和创新能力的欠缺，致使在专业学习阶段数学知识和思维存在欠缺，缺少坚实的数学理论功底，无法创造性地应用数学知识解决工程实践中的问题。

（3）教学模式单一，课程教学单纯以课堂教学为主，课堂教学仅以知识传授为主。传统大学数学教学是以课堂为主的单一型课程教学模式，教学要求统一，缺乏多样性及层次，存在看重古典轻视现代的教学内容，重视连续轻视离散等问题。课程基本按照定义—定理—例题—习题这种传统过时的教学模式。教学缺少工程特征与兴趣开发，不看重课程内部与课程之间的知识耦合关系，不重视学科关联交叉，因此不利于学生知识体系的融汇贯通及交叉运用数学知识的能力提升。

二、新工科视域下的大学数学教学改革路径

新工科建设的主要目标可以表述为：“主动布局、设置和建设服务国家战略、满足产业需求和面向未来发展的工程学科与专业，培养造就一批具有创新创业能力、跨界整合能力和高素质的各类交叉复合型卓越工程科技人才”[2]。根据新工科建设理念和要求，桂林理工大学大学数学教学团队积极开展课程研究和实践，根据新工科背景下大学数学教学需，要根据产业转型升级和社会发展的要求，围绕新专业或专业升级改造对于数学知识、方法、思维和能力提出新的要求，特别是在大学数学教学中需更加注重培养学生的创新思维和实践能力，提高数学对解决复杂工程问题能力的支撑作用。

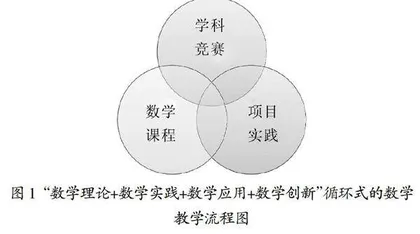
为达到真正意义上的创新型新工科人才培养目的，更需要我们从更高的站位思考整个学科专业的改革、教学方式的升级，以及师资队伍、科研平台的建设[3-4]。经过学校课程团队多年连续不断地研究实践，不断优化课程体系，改革传统的大学数学教育教学模式和课程体系，加强数学应用和实践创新方面的培养。构建了“大学数学理论+大学数学实践+大学数学应用+大学数学创新”循环式的大学数学教育教学流程，凸显“重交叉、优体系、强实践、结专业”的大学数学教育教学特色，如图1所示。学校课程团队、专业老师、校友与企业讨论修定教学大纲，将数学知识分为 A、B、C、D 4个类别，然后根据专业，对类别进行重新组合。A为所有专业必修，B1、B2、B3等为理工科、经管类和文科等专业必修，C类为发展模块，D1、D2、D3等是不同学科考研课程。通过提升教师的工程实践能力，加强实践教学，提高大学数学服务新工科建设的能力。

课程团队不仅要对教学内容进行增、删、改、并等优化与融合，还要协调好课程之间的关系。在课程内容优化方面，课程除了在课程之间的连接和协调方面始终依照专业培养目标进行校正以外，还要在授课案例、课程作业、实践项目及学科竞赛等多个方面进行校正。例如，可以进行授课案例的整合，即依照课程的能力目标要求，对遴拔出的授课教学案例举行深入商讨，根据专业挑选适合的工程案例背景，并将其垂直运用到课程中，不断拓展和深化，培养学生处理复杂工程问题能力，实现知识向能力的转变，更好地应对社会需求。

（一）通过外引内培，重视教师的工程实践能力培养，提升教师将工程实践有机融入数学教学的能力

引进具有工程背景数学教师4人，70%的年青教师具有到企业挂职或出国进修的经历，选派20余名教师参加各类数学应用会议培训。组建学科专业竞赛指导团队，80%的教师参与了“大学生数学建模”“大学数学竞赛”和“大学生创新创业”指导。教师通过开设应用研究型课程提升学科交叉和实践能力。

（二）确立了“课堂为基础、竞赛为牵引、重点在实践”的创新型卓越工科人才培养观

基于新工科建设理念，在以学生为中心，产出为导向的引导下，首先对大学数学内容进行模块化划分，依照专业发展需求开展层次化、模块化的组合教学。基础模块满足各专业对数学课程要求；专业模块由专业、行业、企业和数学老师共同商议决定；发展模块设为公选课，为学生考取研究生继续深造设置。其次开展数学建模、数学竞赛等活动，通过专题讲座、培训和赛前训练等，提高学生的分析、建模、表述和求解的能力，达成“以赛促学、以赛促教”。重视数学实践，使学生经过课程、竞赛和创新创业实践活动，完成从知识接受到知识创造，提升学生实践创新能力。

（三）基于学生发展需求，遵循循序渐进原则，优化课程群，构建“基础课程+综合课程+培训课程+实践课”全贯通的大学数学课程体系

课程体系要重视知识和能力的协调发展，使学生具有更强的社会适应性。注重跨学科课程资源的开发与整合，走开放、融合和自适应的新工科建设之路[5]。根据“基础知识—基础训练—综合知识—综合训练—创新实践”循序渐进原则，设置“基础课程、基础实验、综合课程、竞赛培训、竞赛实践”五个课程教学模块，建成“课程内知识融合、课程之间知识融合、已有知识与拓展知识融合、课内实践与课外实践融合”的大学数学课程体系。设计大一、大二以基础课程、基础实验为主，大二、大三以综合课程、综合训练、竞赛培训为主，大三、大四以竞赛培训、竞赛实践为主的四年全贯通的大学数学课程体系，如图2所示。

（四）基于“知行合一”，形成了“四融合、六结合”的大学数学教学模式

数学不是单独的符号，其来源于实践并应用于实践，才能为新工科专业发展提供更好服务。在注意可教学性的原则下，适当浸透现代数学思想，介绍现代数学术语和符号，为学生将来学习现代数学知识供给对应接口。用现代数学观点实行教学，“为未知而教，为未来而学”，坚持问题导向，致力“教、学、赛、创”四融合联合创新，践行“知行合一”原则。重视“六结合”，即数学与专业、思政结合，教学与科研结合，理论与实践结合，课内外结合，工程素质与创新能力结合。

“教、学、赛、创”四融合联合创新，指引学生深度学习，通过“课堂导入、案例分析、任务过程和考核激励”引导学生进行“自主学习、师生讨论、总结提升和实践训练”的研究性学习。加强运用实例的介绍，特别是来自实际真实问题的解决方法的介绍。不断融入其他学科的前沿知识和动态，注重不同领域新知识、新技术的交叉融合。对传统内容的运用性问题进行更新和补充，如少许传统内容（函数画图、函数逼近和数值计算等）通过运用数学软件加以呈现，让学生上机处理简单的实际问题，以体验到摒弃死记硬背数学公式的学习快感，提升学生的学习兴趣，使学生运用数学的能力逐渐加强。项目驱动教学，将竞赛和创新实践项目内容融入课程中，创设情境，要求学生“真题真做”；引入科研成果，引导学生展开实践创新活动；通过课赛创结合，强化实践，推进知识向实践能力和创新能力的延伸。