思政教育融入数学模型课堂研究

摘  要：数学教育主要是为提高全民的数学素养和思维能力，最终服务于社会，为祖国和人民贡献智慧贡献生产力。数学模型是综合数学与实际问题的一门课程，是应用数学解决实际问题的重要手段和途径。配合现代化教学理念、教学内容、教学方法和手段，以及建立数学模型课程与其他数学类基础课程的联系，提升学生的建模能力，增强学生的成就感与责任感，激发学生服务社会的情怀和信心。

关键词：数学模型；思政教育；价值观；教学目标；教学方式

中图分类号：G641      文献标志码：A          文章编号：2096-000X（2023）03-0163-04

Abstract： Mathematics education is mainly to improve the mathematical literacy and thinking ability of the whole people， serve the society， and make contributions to the country. "Mathematical Model" is a course that integrates mathematics and practical problems. It is an important means to apply mathematics to solve practical problems. With modern teaching concepts， teaching contents， teaching methods and the connection between "mathematical model" course and other basic mathematics courses， can enhance students' modeling ability， students' modeling ability is enhanced， students' sense of achievement and responsibility are increased， and students' feelings and confidence in serving the society are stimulated.

Keywords： Mathematical Model; ideological and political education; values; teaching objectives; education method

课程思政的主要目的是把“立德树人”作为教育的根本任务。我国对学校的思想政治教育工作一直非常重视。2004年，中共中央、国务院出台了加强学校思想政治教育工作的文件《关于进一步加强和改进大学生思想政治教育的意见》。上海首先开始了思政教育的探索之路[1]。2017年，中共中央、国务院印发了《关于加强和改进新形势下高校思想政治工作的意见》。2020年，教育部印发《高等学校课程思政建设指导纲要》，指出“培养什么人、怎样培养人、为谁培养人是教育的根本问题，立德树人成效是检验高校一切工作的根本标准”。可以看到，国家对学生的思想政治教育一直都没有放松。对学生的思想政治教育包括了学生的政治方向、价值取向、人格品质与文化知识等多方面。越来越多的学校、科学门类和教师投入到课程思政的教学模式的研究之中[2-6]。

2017年，教育部高等教育司发布了《关于开展新工科研究与实践的通知》，提出“新工科”教育理念[7]。对人才培养模式、 教育教学的发展体系提出了要求。“新工科”理念的提出对高等教育而言，是挑战也是发展机遇，高等教育对人才的培养模式也应逐步由主要传授理论知识向应用型人才和创新型人才的培养模式转变。

数学模型作为一门多数高校某些工科类专业的必修课程，是理论学习与实际问题的重要桥梁，如何开展数学模型的课程思政，从而更好地为各专业服务为国家服务，是有必要思考与探索的问题。沈阳航空航天大学（下文简称“我校”）数学模型教学团队，结合学校“培养较强工程实践能力和一定创新意识的高级应用型人才”的培养目标和成为“高水平研究应用型大学”的目标，积极配合学校的发展方向，建立起数学与其他学科及实践应用之间的桥梁，开阔学生视野、提升数学的应用能力，从而更好地发挥大学数学教育服务国家战略的功能。数学教育主要是为了提高全民的数学素养和思维能力，最终服务于社会，为祖国和人民贡献智慧贡献生产力。因此，如何在课堂上真正地提高学生的思维能力和创新能力，引导学生敬业爱国是本门课程最重要的问题。多年来，沈阳航空航天大学的“数学模型”教学团队以饱满的热情锐意进取，不断以新时代教育理念为引领，在教学方法、教学理念及教学内容等方面，不断改革创新，与时俱进，以适应时代和学校发展的需要。

一、教学目标和教学方式

每门课程开课的时候，或每位教师在设计教学环节和教学内容时，应首先考虑该课程要达到什么样的教学目标，希望学生从中收获些什么，除了知识点之外，还应该让学生受到哪些锻炼或得到哪些感悟。清楚了这些问题后，根据教学目标制定教学方式，能够更好地实施教学，达到更好的教学效果。我校的“数学模型”课程秉承“以学生的学为本”和“教而无类”的教育理念，在以“学”中心的前提下，学生在课堂上的行为是自由的、活跃的，教师公平客观的，在提高学生的思维能力和创新能力的同时，引导学生敬业爱国、服务社会的理念和信心是本门课程最重要的目标。数学模型课堂主要的特点可以概括为：翻转式，汇报式，答辩式，开放式。

（一）课程的总体安排体现教学目标

在开学初，制定好教学的总体安排，包括每周的授课内容，翻转式课堂开展的时间和内容，学生汇报的题目和时间安排，以及中期报告的开展时间与题目设置、上机时间安排、考核方式等。比如，第1周，主要介绍初等模型，使学生对数学建模有基本的认识；从第2周以后，陆续讲解数学模型不同的专题内容，每次课留10 min给学生汇报作业情况；第5—7周，布置中期报告题目10～15个，自由选择，每人独立完成模型、建立、软件的使用和论文的撰写等，要求同学们在课堂上汇报成果，目的是全面锻炼学生的建模能力；第10—11周，布置期末报告题目，3个人一组，为学生参加建模竞赛打下基础，并培养学生的团结协作能力；第12周，进入答辩环节。

（二）教学方法体现教学目标

本校信息与计算科学专业每届招收1～2个班级，约30～70人。很适合开展课堂讨论等环节，每次课留出10 min给学生汇报，其余师生共同参与讨论，学生汇报和讨论的形式主要有以下几种。（1）翻转式课堂。事先布置好自学任务与实际问题，课堂上，让学生汇报实际的建模过程与求解结果等，通过比较不同学生的模型结果的差异性，学生共同讨论：哪个是正确哪个是最好的、该方法到底该如何使用等。这样让学生从根本上弄清自学内容。（2）个人汇报。每次布置的作业都是一些建模问题，每个人的建模方案都有所不同。学生在汇报自己的建模思想的时候，能更加理清自己解决问题的思路，其余的同学也学习到了新的建模方法，并且可以对报告内容提出疑问，使解决问题的方法更加广泛和深入。（3）小组汇报。学生的期末报告3人一组，在结课前一周完成。小组以答辩的形式在课堂上向大家汇报建模成果。这不仅营造了“师生互动，生生互动”的氛围，更增强了小组成员的责任感，各负其责，形成团队意识和合作意识。

同时，借助现代化教学工具可以加强师生互动。雨课堂的主观题、客观题、投稿及随机点名等，吸引了更多学生参与课堂互动，教师及时了解学生的学习效果，有针对性地进行授课；QQ群方便上传材料，教师可以将课外的辅助材料数学史、数学文化和数学模型等资源上传，学生也可以将自己感兴趣的与本课程相关的内容上传，这样就达到了师生资源共享、共同学习、共同进步的目的。

每次的作业、中期报告、期末报告都有课堂展示环节，几乎每次课都有学生上讲台与大家分享建模思想和方法；同时，每节课的随机点名、弹幕与雨课堂题目的设置等，让更多的同学参与，将更多学生的思想和能力展示给大家，增加了学生学习的热情和动力。学生参与课堂常态化，实现“生生互动”“师生互动”，体现课堂是“学生的课堂、辩论的课堂”。

（三）课堂的总体安排

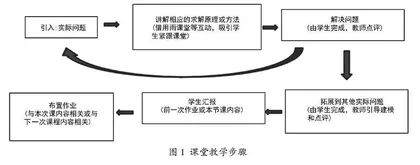
课堂是教学环节中最重要的一环，是实现教学目标的最主要的方式。因此课堂的设计是至关重要的，教师在上课前除了准备好讲课内容之外，还需要设计课堂中的各个教学细节，包括：在哪些地方提问，学生的回答方式是抢答还是随机点名，哪些地方设置主观题与客观题，在哪些地方设置弹幕，哪些地方需要板书，哪些板书内容是随时可擦掉、哪些内容是需要保留在黑板上的，以及黑板如何规划等等，这些都需要事先设计好。一般情况下，课堂教学步骤如图1所示。

下面，以规划模型课堂为例，具体介绍课堂的实施过程。（1）教学背景。学生已经学过matlab，学生已知线性规划的结构。（2）事先准备。上一节课程的末尾已经简介了“线性规划”模型，布置作业为“自己完成线性规划的matlab求解方法与下载lingo软件”；告知学生下节课带笔记本电脑上课；教师在教室电脑上安装好软件。（3）备课。熟悉教学内容；理清教学重点与难点；设计板书的内容；设计提问的地方与内容；提问的方式；设计让学生演示的内容；准备好习题和作业。（4）讲授线性规划。①复习“线性规划”模型的结构与特点；②以三个引例作为模型的实际背景和问题的引入，以提问的方式，配合板书与同学们一起完成，检查学生对线性规划模型的掌握情况；③讲解灵敏性，配合引例中的问题，让学生对灵敏性在实际问题中的意义有较为清晰的认识；④介绍matlab软件和lingo软件，教师在教室演示，带领同学们一起操作；⑤“自来水问题”作为课堂练习，让学生自己完成。（5）讲授非线性规划。①从“钢管下料”实际问题出发，让学生自己设置自变量与目标函数，并体会到理解题目或解决的入手点不同，就会有不同的数学模型，也可借这个模型，让学生体会数学模型的发散性思维和创新性思维；②归纳非线性规划的结构和特点；③让学生自己找约束条件，并用matlab对引例求解，发现非线性规划的解是依赖初值的。让同学们思考“那么如何能较为准确地得到结果呢？”教师给出结论：缩小可行域。让同学们进一步挖掘暗藏的约束条件，最后教师给出约束条件的答案，再一次用matlab求解，结果较好。这个过程学生们能体会到非线性规划求解的困难和方法，也教育学生要有孜孜不倦的专研精神；④思考“汽车制造问题”，为下节课讲解“整数规划”做铺垫。（6）教师反思与总结教学内容和教学方法上的优点和不足，在PPT和教案上标注或修改。学生经历了将实际问题转化为线性规划问题并求解的过程，发现新问题，建立了非线性规划模型并求解的过程，学生参与了整个教学过程，注意力始终在课堂上，实现了锻炼学生建模能力的目标，并加强了“用知识服务社会”的信心和责任感，也体现了“奋斗创造幸福”的成就感和价值观。

（四）课程成绩评定方式

授课过程中，学生主要完成两次较为正式的数学模型报告：中期报告“一人一题”，期末报告“一组一题”，题目本身有难易差异，以适合不同层次的学生。结合学生的完成情况与题目的难易程度，给报告打分。除此之外，每次的作业和课堂练习中，学生多次完成了小型的建模题目。学生最终成绩由课堂表现、两次报告等综合表现来评定。开放式的考核标准综合的评价了学生的努力程度、学习效果和建模能力等多方面的能力，形成了多元的考核方式。

（五）课程思政的体现

我校教学团队一直以在教学过程中潜移默化的将文化和情怀传递给学生，做到以“润物细无声”为努力的方向。教师在教学设计上，考核方式上，层层递进，潜移默化中实现了对学生思想政治、爱国情怀、性格和品质的磨练。在讲解具体方法的时候，对该方法或对应的问题“追根溯源”提高学生的数学素养和数学文化水平；把社会热点问题引入课堂，并利用建模方法加以解释、分析或解决，将社会责任感、价值观和幸福观在潜移默化中传递给学生。增强学生爱国热情和服务社会造福人民的信念和信心。培养了学生面对实际问题时，不骄不躁，逐步深入，形成“用知识服务社会”和“奋斗创造幸福”的理念和信心。

二、教学内容常更常新，与时俱进

目前，大多数的数学模型教材，均介绍以下几部分内容：初等模型，微分方程模型，稳定性模型，图论，最短路问题和随机模型等[8-9]。虽然每部教材具体所选的具体的知识点和具体的实际问题不尽相同，但具体介绍的模型与问题大致相近。随着社会和科技的进步，涌现了大量的新问题和新方法，对学生的建模能力与数学模型课程提出了巨大的挑战。为适应新挑战、新问题和新形势， 课程中适当加入社会的热点问题，带领学生一起讨论和寻求解决方案，对锻炼学生的能力，有益于提高学生服务社会的情怀。因此，这关注课本的知识是远远不够的。为了跟随时代的前进脚步和提高学生的能力，本校的“数学模型”教学团队，综合参考和钻研多本教材，多方了解其他学科的问题和方法，将新问题和新知识引入课堂。几乎每年都对教学内容做或多或少的调整。近几年，陆续增加主要的内容有主成分分析、spss软件、灰色预测、Topsis、模糊综合评价、生境质量Invest模型、Invest软件、感知机、K近邻法及朴素贝叶斯方法等。其中Invest模型是生态学里评价某个地区生态环境的较为先进的方法；感知机和K近邻法是统计学习的基本方法。体现了多学科与多种专业的融合，让学生切实感觉到数学应用的普遍性和重要性。目前我校团队的数学模型课程的授课内容主要包括：优化模型类，微分方程模型类，稳定性模型类，图论类，随机模型类，最短路问题类，预测模型（主要介绍数据的相关性分析、马尔萨斯模型、Logistic模型、灰色预测模型等），统计与分类模型（主要介绍聚类分析、感知机、K近邻法，贝叶斯方法等），生境质量模型（主要介绍生态学中评价生态环境的Invest模型）。