数学跨学科综合与实践活动设计：一种思路和一个案例

摘 要：设计数学跨学科综合与实践活动有多条路径，但教师需要循序渐进地积累经验，不妨从聚焦特定人、物、事的跨学科观察开始。以“身边之物”为起点依次开展物理观察、数学抽象和美术创作是一种思路：不但操作性强，而且能令学生感受到“数学无处不在”；而物理和美术作为所跨的学科，与数学的联系可谓“一近一远”，近显差异、远见关联，可以为学生认识数学和数学学习提供新的视角。按照这一思路，以“一张A4纸”为载体设计数学跨学科综合与实践活动，还能提升学生对测量、维度、比例、对应等重要数学概念的认识。

关键词：数学教学；跨学科；综合与实践；A4纸

强化义务教育课程的综合性与实践性是进一步深化课程改革、推动育人方式变革、助力学生核心素养培养以及实现基础教育高质量发展的重要策略。^［1］作为课标修订的主要变化之一，《义务教育数学课程标准（2022年版）》对综合与实践领域的内容和教学强调了“跨学科”，要求教师“以培养学生综合运用所学知识和方法解决实际问题的能力为目标，根据不同学段学生特点……适当采用主题式学习和项目式学习的方式，设计情境真实、较为复杂的问题，引导学生综合运用数学学科和跨学科的知识与方法解决问题”^［2］，“通过综合运用数学和其他学科的知识与方法解决真实问题，着力培养学生的创新意识、实践能力、社会担当等综合品质”^［3］。

跨学科学习的实质在于以开放的态度泛化边界，以某一学科知识的所见所能去弥补另一学科知识的所不见所不能。事实上，面对跨学科学习，大部分教师都需要重新适应，甚至由于长期单学科钻研，比学生更难适应。数学跨学科综合与实践活动的设计与实施，将为教师和学生从更广阔的视角重新认识数学、体会数学学习，创造新的契机。当前，如何基于不同学科的内在关联，设计突出数学思维的综合与实践活动，是中小学数学教师和数学教育研究者面临的共同挑战。^［4］我们认为，设计数学跨学科综合与实践活动有多条路径，但教师需要循序渐进地积累经验，不妨从聚焦特定人、物、事的跨学科观察开始。本文尝试给出一种思路及一个相关案例，供大家讨论。

一、思路：以“身边之物”为起点依次开展物理观察、数学抽象和美术创作

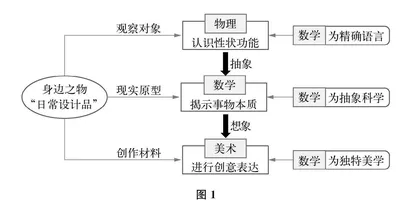
具体地说，先选择“身边之物”为观察对象，鼓励学生从物理视角认识其基本属性，通过细致的测量和必要的运算，刻画其物理属性，培养自觉的数量观念，体会数学作为科学语言的作用；再以“身边之物”为现实原型，引导学生剥离其物理属性，形成数学的研究对象，探索揭示“此物之所以有此形态功能”背后的数学本质和依据，在经历“横向数学化”（弗赖登塔尔语）的同时，体会数学学习和物理学习的区别，明确数学研究对象的理想化和抽象性，进而感受数学应用的广泛性；最后用“身边之物”为创作材料，以特定数学概念为创作主题，激发学生想象并形成美术作品，体会数学在美术创作中的重要作用，并从另一个角度欣赏数学之美。该设计思路的要领与流程如图1所示。

（一）为什么以“身边之物”为思考起点

环顾四周，各类日常生活物品平凡却不普通，每一件都是“设计品”。它们之所以保留“此形此态”，是为了满足特定功能不断被优化的结果。以桌面为例，为什么常为矩形或圆形，少有三角形或其他形状？若考虑桌面本身，则围坐人数和人均使用面积是两个关键的功能指标，这里自然涉及不同形状图形周长和面积之间的关系。若考虑桌子与环境的互动，则可能要求桌面配合空间灵活使用（如靠墙摆放无缝隙）且桌角安全隐患小。当桌子与特定的人关联时，又要根据个人喜好需求定制。如某好客的主人想系统设计全屋的桌子，使得各个桌子平时分散于不同房间使用，必要时拼合为一，那么，设计两张全等的直角三角形桌子平时分置于房间墙角，是不错的灵感。总之，鼓励学生用数学的眼光观察现实世界时，不妨从“身边之物”开始。这样不但操作性强，而且重新认识“老朋友”的惊喜更能令学生感受到“数学无处不在”。

（二）为什么选物理和美术为所跨学科

明晰学科的研究对象从哪里来，进而欣赏学科的研究方法，是学科教学希望带给学生的认识和思考。数学源于对现实世界的抽象，是人们认识、描述和解释现实世界的重要方式。但学生在学习过程中，鲜有机会深刻体会数学研究的“数”和“形”是人类想象的成果，在现实世界中并不存在。数学家保罗·洛克哈特曾说，他“永远无法把圆拿在手上，却可以将其悬于脑中”^［5］。想要理解这句话以及作者言说时的欣喜和骄傲，学生可能要经历一个完整细慢的“识物并抽象”的过程。

物理学是研究物质基本结构、相互作用和运动规律的一门基础学科。学习时，学生首先要能认识物体形状、薄厚、轻重、颜色等外部特征，学会通过简单仪器测量并定量描述物体的长度、质量、体积、密度等性质，在此基础上进一步探讨“结构与功能”等跨学科概念。其中，测量是重要的物理活动，亦是重要的数学活动，贯穿基础教育阶段的数学和物理学习。^［6］在测量“识物”的过程中，学生能感受数学作为科学语言描述的精确性，同时发现工具对测量的限制，以及测量结果总是一种近似的事实。这些活动经验将促进学生思考现实物品和理想模型的区别。事实上，越是细致探究物体的物理属性，越能发现现实世界的复杂多变，越能感悟数学世界的纯粹精准。

相较于物理学与数学的亲密，美术似乎离数学较远。具体到基础教育，如何提升美术（艺术）特长生的数学成绩已受到广泛关注，而理科生美术经验缺乏似乎并不是问题。美术学习中，学生根据自己的想象和构思，用纸、泥等材料，绘、折、叠、组合等方法，对称、重复、对比、比例、变化、统一等形式原理，创作出平面和立体造型的作品。这是培养想象力和创新思维的重要途径。由此也能发现数学的知识和方法在美术创作中的重要运用。比如，比例、透视等是画家写实创作的工具，密铺、无限等是艺术表达的主题。已有研究证明，在数学和美术整合的课程中学习，能促进学生运用数学词汇沟通表达，产生学习数学的积极情感，体会数学之美。^［7］

综上，数学跨学科综合与实践活动设计可以选择物理和美术作为所跨的学科，因为它们与数学的联系可谓“一近一远”，于近处显差异，于远处建关联，可以为学生认识数学和数学学习提供新的视角。

二、案例：一张A4纸的故事

A4纸是典型的“身边之物”，对学生而言熟悉易得。作为特定规格的纸张（连同ISO 216定义的另外的B、C两组纸张），其定各、定量都有可挖掘的数学信息。事实上，中小学数学教材和试题中常见矩形纸张的身影。例如第一学段的看纸张厚度估计张数、测量折痕长度，第二学段的折纸平均分、找对称轴，第三学段的了解立体图形展开图并计算表面积，第四学段的制作无盖纸盒，等等。上述问题情境虽未明确说明纸张尺寸，但在学生脑中多与A4纸的形象重合。在数学课上，学生操作或想象时，可能并不区分A4纸是现实世界中的三维物体，还是数学世界中的理想矩形。类似地，在美术课上，学生或在纸上画出立体效果，或用纸折叠出立体造型，但对其中所涉及的维度转化可能并不注意。因此，以“一张A4纸”为载体，经由“物理观察—数学抽象—美术创作”，设计数学跨学科综合与实践活动，不但能从不同学科视角引导学生系统认识现实生活中的“某物”，让学生体会运用数学语言刻画的精确优势、得到数学研究对象的抽象过程、数学与美的丰富关联，还能提升学生对测量、维度、比例、对应等重要数学概念的认识。根据这一思路设计的“一张A4张的故事”活动的要点与阶段如下页图2所示。

（一）对“一张A4纸”的物理观察

第一阶段，以“一张A4纸”为观察对象。教师准备附近文具店中学生常见的各类纸张，让学生在对比过程中得到形状、大小、颜色、重量、材质等属性，再想办法测量不同属性并列表描述。同时，教师将各类纸张及其包装封面（含规格信息）提供给学生参考。在测量的过程中，引导学生发现：一张A4纸（如70g/m²）尽管很薄，但仍然是有厚度的，推而广之，现实生活中的实物都是三维的存在；所谓的“长”“宽”“厚”本质上都是一维线段的长度，面积、体积和密度则可以看作相关属性数值运算的结果。此外，某些物理属性（如纸张耐折度）的测定要转化为特定行为（如在恒定力条件下往复折叠直至断裂）的次数，仍然用数来刻画。事实上，对具体物品的认识要关注其各种物理属性，对不同属性的描述和比较最终也体现为数（或其运算结果）与其大小关系；属性测量（测定）受工具的限制，结果都是在可接受范围内的近似估计。

（二）对“一张A4纸”的数学研究

第二阶段，以“一张A4纸”为现实原型。在学生充分感受现实世界中一张A4纸的复杂后，教师引导学生在头脑中想象数学世界中的矩形：颜色、材质等属性被剥离，厚度也不存在，唯有平面内的图形形状和大小。然而，以A4纸为原型抽象得到的这个数学研究对象，为什么选择为矩形？那么多矩形，又为何选择长为297mm、宽为210mm的？再回到A4纸的命名，为何是“A”不是“B”，有“C”吗？为何是“4”不是“1”，有“-1”吗？原来，为了满足在复印过程中放缩不变形这一良好功能，系列纸张的长宽比须为2；而“4”不仅表示以A0纸为起点对折的次数，也说明2⁰张A0纸对应2⁴张A4纸。在不断关联现实原型和数学对象，讨论其功能与结构（这里特指形状和大小）的过程中，“此物之所以此名、此形、此量”背后的数学道理也愈加明晰。最后，桌子上的这张A4纸对折不了几次，而脑中那张“A4纸”就能自由操作，将其对折42次轻轻松松，但真能抵达月球吗？又将展开一系列有趣的讨论。

（三）对“一张A4纸”的美术创作

第三阶段，以“一张A4纸”为创作材料。再次回到现实生活，聚焦一张普通的A4纸，教师让学生回忆用它做过什么，想象用它还能做什么，能否创作出“一张A4纸的故事”。事实上，A4纸是探索并理解维度概念，沟通一维、二维、三维空间，区别现实世界和数学世界的绝佳素材。纸的边缘（长、宽、厚）、折痕，以及在纸上所画的直线段都可看作一维长度。学生在纸上绘画，一方面，可以通过透视关系展现三维空间效果；另一方面，随着笔触压痕或颜料堆叠，又在另一个观察尺度下形成平面上的沟壑万千或层峦叠嶂。此外，不经意间对纸的卷曲、折叠或撕扯，又实现了维度的升级。如何以“维度”为主题讲出“一张A4纸的故事”，学生可以有众多的选择。在创意过程中，数学和美术之美、实践和想象之趣会在不同的时刻碰撞激发。

此外，对于“一张A4纸”，如果进一步探索，教师还可以围绕折纸活动设计STEAM背景的任务。^［8］当然，除了“一张A4纸”，还可以探究“一根绳”“一个包装盒”“一块蛋糕”的故事。随着学生活动经验的积累，数学跨学科综合与实践活动的设计也可以从研究静态的单个物体转向由多个物体或部分组成的系统及其变化。再进一步，除了“物”，还可以围绕“人”“事”“景”设计活动，鼓励学生用数学的眼光、思维和语言来观察、思考和表达现实世界。

参考文献：

［1］中华人民共和国教育部.义务教育课程方案（2022年版）［S］.北京：北京师范大学出版社，2022：前言2.

［2］［3］中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022：16，87.

［4］郭衎，曹一鸣.综合与实践：从主题活动到项目学习［J］.数学教育学报， 2022（5）：9-13.

［5］P.Lockhart.Measurement［M］.Cambridge，MA：Harvard University Press，2012：1.

［6］詹善生，汤金波.“长度的测量”：从生活到应用——物理跨学科实践探索一例［J］.教育研究与评论（中学教育教学），2023（3）：84-89.

［7］M.Kus，E.Cakiroglu.Mathematics in the informal setting of an art studio：students’ visuospatial thinking processes in a studio thinking - based environment［J］.Educational Studies in Mathematics，2022（3）：545-571.

［8］唐依婷，袁智强，戴飒英.开展跨学科STEM教学，培养对数学的好奇心——《翻转的数学》教学及启示［J］.教育研究与评论（中学教育教学），2022（5）：74-81.