初中数学教学中抽象能力的培养

摘  要：抽象能力是初中阶段数学核心素养的主要表现之首。抽象能力主要表现在两个基本方面：数学知识都是抽象的结果；抽象的数学知识能广泛地用于解决实际的问题。在初中数学教学中，培养学生的抽象能力，基本的做法是，引导学生在知识的形成过程和问题的解决过程中，感悟抽象方法：舍弃物理背景，得到数学概念及其关系；舍弃个别的非本质特征，得到共同的本质特征。

关键词：抽象能力；初中数学；知识形成；问题解决

一、 对抽象能力的再认识

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）将抽象能力作为初中阶段数学核心素养的主要表现之首，并指出：“抽象能力主要是指通过对现实世界中数量关系与空间形式的抽象，得到数学的研究对象，形成数学概念、性质、法则和方法的能力。能够从实际情境或跨学科的问题中抽象出核心变量、变量的规律及变量之间的关系，并能够用数学符号予以表达；能够从具体的问题解决中概括出一般结论，形成数学的方法与策略。”［1］

数学是研究数量关系和空间形式的科学［2］，数学中的抽象是对“数量关系与空间形式”的抽象，首先就要“舍弃事物的一切物理属性，抽取出数学概念及其关系”［3］。进一步地，什么是抽象呢？新课标的解读指出：抽象是指从众多事物中舍弃个别的非本质特征，抽取出共同的本质特征（共同特征就是本质特征）。［4］显然，最初的抽象是基于直观的，而且，抽象是理性思维的基础——事实上，人类的一切知识都是从直观开始的，从那里进到概念，而以理念结束［5］。

可见，抽象能力主要表现在两个基本方面：一方面，从概念（研究对象）到命题（研究结果，即规律结论，包括定理、公式、性质、法则和方法、策略等），数学知识都是抽象的结果［6］，在现实生活中并不存在，且具有较强的一般性；另一方面，抽象的数学知识能广泛、高效地用于解决实际而具体的问题。

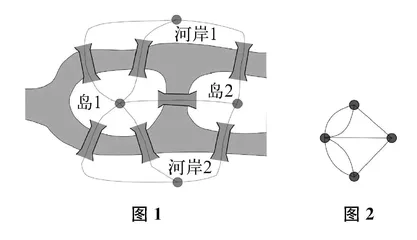
一个典型的例子是，欧拉为了解决“七桥问题”，发现了有关“一笔画”的知识。根据数学家徐利治的考察［7］，欧拉当时是这样想的：问题中的河流、桥、岛、河岸都不是本质的，本质的东西只有点、线以及它们之间的关系。于是，欧拉把人步行过桥的问题（如图1所示）抽象成一个几何图形问题（如图2所示）。欧拉通过进一步的分析，证明了图2不是一笔能画出的图形，从而获得了“七桥问题”的最终解答。

二、 抽象能力的培养

结合抽象能力表现的两个基本方面，我们认为，在初中数学教学中，培养学生的抽象能力，有两个基本的做法：

（一） 在知识的形成过程中培养

数学知识都是抽象的结果。因此，在教学中，教师要贴近学生的现实选取或设计情境背景，提出相关的问题（最好是递进的系列问题），引导学生从感性到理性，经历知识的形成过程，感悟其中的抽象方法：发现数学概念及其关系，发现共同的本质特征。

【案例1】平行四边形定义的教学

平行四边形的概念在小学和初中都要学习，但要求不一样：在小学，要“能辨认平行四边形，能直观描述其特征”［8］；在初中，要“理解平行四边形的概念以及相关概念之间的关系”［9］。前者是“了解”层次的要求，即“从具体实例中知道或举例说明对象的有关特征；根据对象的特征，从具体情境中辨认或举例说明对象”［10］；后者是“理解”层次的要求，即“描述对象的由来、内涵和特征，阐述此对象与相关对象之间的区别和联系”［11］。

因此，初中教学平行四边形的概念，要引导学生经历平行四边形定义的形成过程，感悟其中的抽象方法。具体可以贴近学生的现实，设计“观察图3所示的六个四边形”的情境背景，提出如下系列问题，引导学生感悟“舍弃个别的非本质特征，得到共同的本质特征”的抽象方法（基于学生已有“舍弃物理背景，得到数学概念——几何图形”的抽象经验，可以略过这一抽象过程，提高教学效率）。

问题1：你有什么发现？

问题2：你能说出图形②③⑤⑥有哪些图形①④没有的共同属性吗？

问题3：上述共同属性之间有什么关系？

问题4：如何给这类图形下定义？如何给这类图形起名称？

问题1是一个发散性问题。学生的发现可能比较多，如：（1） 它们都是四边形；（2） 内角和都是360°；（3） 都有两条对角线；（4） 图形①没有对边相互平行；（5） 图形④有一组对边互相平行；（6） 图形②③⑤⑥有两组对边互相平行……

当学生发现结论（6）后，教师可以及时提出问题2。问题2也是一个发散性问题，但相对于问题1，发散“范围”有所减小，目的是引导学生“舍弃个别的非本质特征，得到共同的本质特征”。学生通过讨论、交流，可以得到以下共同属性：两组对边分别平行、分别相等，两组对角分别相等，每组邻角分别互补，对角线互相平分……

问题3引导学生理清“共同的本质特征”之间的关系。在教师的点拨下，学生能够发现：在四边形的条件下，“两组对边分别平行”“两组对边分别相等”“一组对边平行且相等”“两组对角分别相等”“所有邻角互补”“对角线互相平分”等共同属性任意两个之间存在相互推出的关系；同时“一组对边平行，另一组对边相等”“一组对边相等，一组对角相等”等共同属性推不出上述共同属性。

得到了上位概念（属）下的本质特征（种差），便可以采用“属+种差”的方式下定义。理清了本质特征之间的关系，便可以利用“最基本”（可以推出其他本质特征）的本质特征下定义。对于问题4，教师可以引导学生分别利用“两组对边分别平行”“两组对边分别相等”“一组对边平行且相等”“两组对角分别相等”“每组邻角分别互补”“对角线互相平分”等“最基本”的本质特征给这类图形下定义，然后比较发现“两组对边分别平行”这一本质特征“更明显（直观）”，从而引出习惯上采用（而非唯一）的定义“两组对边分别平行的四边形”和名称“平行四边形”。

这样的教学引导学生经历了平行四边形定义的形成过程，不仅可以帮助学生感悟重要的抽象方法，而且帮助学生充分理解平行四边形的概念，建立平行四边形概念的CPFS结构［12］。

（二） 在问题的解决过程中培养

抽象的数学知识能广泛、高效地用于解决实际而具体的问题。因此，在教学中，教师要从生产生活的各个方面、科学研究的各个领域广泛选取或设计真实可信的实际问题，引导学生建立数学模型，利用数学知识处理数学模型（如推理、计算等），回到实际意义（包括验证），经历问题的解决过程，感悟其中的抽象方法，特别是舍弃物理背景，得到数学概念及其关系（尤其是数量关系）。

【案例2】“购书费用问题”的教学

在学生学习了分式方程、一元一次不等式以及一次函数的知识后，教师可以设计如下“购书费用问题”，引导学生经历运用数学知识解决实际问题的过程，感悟“舍弃物理背景，得到数学概念及其关系——数量关系”的抽象方法。

《周髀算经》《孙子算经》是我国古代较为普及的算书。某书店出售这两种图书，《孙子算经》的单价是《周髀算经》的34，用600元购买的《孙子算经》比《周髀算经》多5本。

（1） 两种图书的单价分别为多少元？

（2） 某校计划到该书店购买这两种图书共80本，且所购《周髀算经》的数量不少于《孙子算经》的一半。由于购买量比较大，书店对两种图书均按八折出售。两种图书分别购买多少本时，总费用最少？

运用数学知识解决实际问题的关键是建立数学模型，建立数学模型的过程就是数学抽象的过程。教学中，教师要重点引导学生由题目条件抽象出数学模型——

第（1）问中，条件“《孙子算经》的单价是《周髀算经》的34”舍弃物理背景，抽象成数学模型，即数量关系y=34x（x元是《周髀算经》的单价，y元是《孙子算经》的单价） ；条件“用600元购买的《孙子算经》比《周髀算经》多5本”舍弃物理背景，抽象成数学模型，即数量关系600y-600x=5。由此，代入消元后，利用分式方程的知识便可解决问题：《周髀算经》的单价是40元，《孙子算经》的单价是30元。

第（2）问中，条件“某校计划到该书店购买这两种图书共80本”舍弃物理背景，抽象成数学模型，即数量关系m+n=80（m是所购《周髀算经》的本数，n是所购《孙子算经》的本数）；条件“所购《周髀算经》的数量不少于《孙子算经》的一半”舍弃物理背景，抽象成数学模型，即数量关系m≥12n；条件“两种图书按八折购买的总费用”舍弃物理背景，抽象成数学模型，即数量关系w=32m+24n（w元为两种图书按八折购买的总费用）。由此，代入消元后，可以先利用一元一次不等式的知识，得到整数n≤1603，即n≤53；再利用一次函数的知识，得到w=-8n+2560≥-8×53+2560=2136（当且仅当m＝27、n=53时“=”成立），从而解决问题。

参考文献：

［1］［2］［8］［9］［10］［11］ 中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022：8，1，28，66，181，181.

［3］ 张金良.解密数学抽象  探索教学策略［J］.数学通报，2019（8）：2326+66.

［4］ 史宁中，曹一鸣.义务教育数学课程课标（2022年版）解读［M］.北京：北京师范大学出版社，2022：67.

［5］ 史宁中.数学基本思想18讲［M］.北京：北京师范大学出版社，2016：2.

［6］ 鲍建生.数学核心素养在初中阶段的主要表现之一：抽象能力［J］.中国数学教育，2022（9）：49+13.

［7］ 徐利治.数学方法论选讲［M］.武汉：华中工学院出版社，1988：11.

［12］ 傅赢芳，喻平.CPFS结构理论及其对数学概念教学的启示［J］.教育研究与评论（中学教育教学），2020（6）：2833.