指向思维进阶的小学数学表达课堂范式微探

［摘 要］思维是内隐的，但学生可以借助数学表达使其外显。学生的思维层级决定了其数学表达的层级。文章对学生的数学表达进行研究，变革数学课堂教学模式，不断推动学生的数学表达从“经验性”进阶到“多元性”“结构性”“应用性”，使学生的思维从“前结构”向“拓展抽象结构”水平不断进阶。

［关键词］数学表达；思维发展；课堂教学

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）02-0018-06

《义务教育数学课程标准（2022年版）》指出，数学课程培养学生的核心素养，主要包括会用数学的眼光观察现实世界、会用数学的思维思考现实世界、会用数学的语言表达现实世界。这就表明，数学表达是数学观察、数学思考的结果，也是数学思维的过程与反映。数学表达展现学生思维的同时，也推动学生的思维由低阶向高阶发展。

一、课堂中的数学表达和思维进阶的内涵探析

数学表达是以文字语言、符号语言和图形语言为载体进行的书面或口头交流活动。根据问题解决程度的不同，笔者将学生的数学表达分为“经验性”“多元性”“结构性”“应用性”四个表达层次。随着学生对数学知识的深入理解，其数学表达从外显向内隐推进，其思维从低到高，呈持续进阶状态，这就是学生思维品质的进阶提升过程。根据SOLO分类理论，笔者将水平分为“前结构”“单一结构”“多元结构”“关联结构”“拓展抽象结构”五个阶层，让学生在数学课堂学习中不断成长，促使其思维品质不断提升。

二、课堂中指向思维进阶的教学结构模型探构

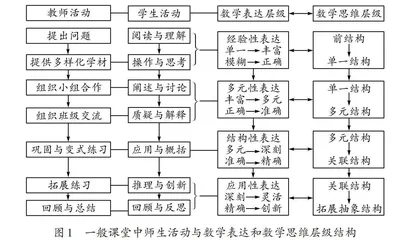
在小学数学课堂教学中，教师与学生各自的行为活动之间既有联系又有区别。不同的数学表达，依照课堂的教学活动推进都可以归结为层层递进的思维层级。在小学数学教学实践和研究中，笔者根据自身经验将一般数学课堂教学分为“教师活动”“学生活动”“数学表达层级”“数学思维层级”四个方面，以纵向的时序构建了教学结构（如图1）。

三、课堂中数学表达促进学生思维进阶的策略探究

一般来讲，在小学数学课堂教学活动中，师生课堂的数学表达有着经验性、多元性、结构性和应用性四个水平层次（由低到高）。每个层次都着意于提升学生数学表达思维层次水平，促进其思维进阶。

（一）经验性表达：开思维进阶之门

经验性表达指学生基于自己的学习和生活经验，通过数学操作解决数学问题，并能够正确表达解题的过程。经验性表达是一种自我表达，有较强的个体性和主观性。经验性表达就是让学生对数学知识进行相关操作、演示、实验、交流等与数学表达的相关活动，在从无到有、从缺乏到丰富、从混乱到有序、从模糊到正确中获取经验，为学生开启思维进阶之门。面对新的数学问题，学生的数学操作经验能为其快速解决问题。丰富的经验性表达，可以为学生思维进阶积累素材并打下坚实的理论基础。

在解决新的数学问题过程中，学生不断获得新的解题经验和丰富的知识经验。在数学经验性表达中，学生在获得多种解题方法的同时，可以促进自身数学思维水平的提升，从“前结构”水平发展为“单一结构”水平，甚至是更高层次的结构水平。数学课堂的经验性表达有以下作用和获取途径。

1.大问题引领：提供数学表达载体

首先，教师设计好大问题，给予学生数学表达的空间。学生独立思考，尝试解决问题，即对数学问题的经验性表达。教学中教师设计的大问题，能为学生的经验性表达打开大门，提供表达载体。

例如，教学一年级认识人民币“元角分”一课，如果按照教材呈现问题，应该是先让学生逐一认识1元以内的人民币，再将其他面值的人民币呈现出来，并询问学生各面值是多少以及是如何辨别的。面对这样的数学问题，学生只能顺着教师的问题，进行单一的、碎片化的数学表达。在这个过程中，学生处于被动性应答，参与的积极性不高，其思维难以进阶。如果将教学流程改用问题来引导，如“你能从这些人民币中拿出1元2角吗？”“比一比，谁的拿钱方法多？”等，促使学生在问题的引领下解决问题，从而认识人民币，并使思维从“前结构”水平进阶到“单一结构”水平。

其次，创设真实的问题情境能帮助学生理解数学知识的意义。如果教师将数学知识呈现得过于抽象，数学知识与学生的生活实际联系不紧密，就会使学生难以真正理解数学知识的现实意义。学生的数学表达是具体的、现实的，给学生营造和生活实际相关的情境，有助于学生理解数学问题且能有效驱动学生的数学表达。

又如，教学三年级“两位数乘整十数”一课时，教材情境图充分关注学生已有的生活经验和知识基础，为学生的数学表达拓展空间。

如图2所示，每盒有12个苹果，10盒有多少个苹果？

①横着看，可以用12×2×5计算；

②竖着看，可以用12×5×2计算；

③已经放好9盒，正在搬最后一盒，可以用12×9+12计算；

④借助已有经验，可以用12×1，再在积的末尾添上1个0；

⑤可以在每盒中先放10个，然后再放2个，即用10×10+2×10计算。

这样的情境可以为学生的数学表达提供多种可能。丰富多样的数学表达，有助于学生拓宽思维空间。

2.多学材选择：丰富数学表达路径

如果说情境激发了学生学习的兴趣，那么多样化的学习材料则是激发学生探索问题的欲望。探索是学生主体性发展的过程，意味着学生的认知能力、情感体验、控制能力均在提高。教师提供多样化的学习材料，能让学生产生多样化的解题思路，助力其自主探索。

例如，教学一年级“9加几”一课，在进行“9+4”的算法探索时，笔者提供了小棒、计数器、十格图、标有数字的纸条尺等多种学具。学生借助丰富的学具，表达了更加丰富的解题思路：

①用小棒摆，先摆9根，再摆4根，接着从4根中拿1根和9根合在一起变成10根，10根和3根合起来是13根；

②用计数器在个位上先拨9颗珠子，再拨4颗珠子，由于个位上的珠子数超过了10，需要向十位进1，进位后，个位上只剩3颗珠子，十位上增加1颗珠子，表示13；

③用十格图表示，已经有9个了，先从4里面给1个凑成10个，格子外面还有3个，合起来是13个；

④用标有数字的纸条尺数，从9往后再数1个纸条尺是10，再数3个纸条尺就是13。

多样化的学习材料，能让学生的数学表达更加丰富。

3.重操作后的表达：明确数学表达指向

操作行为也是一种表达，让学生用语言或自己在内心再次描述操作过程，如同放电影似的进行回放，有助于学生整理思路和自我反思，从而让混乱的表达变得有序，让模糊的表达变得正确。

例如，教学“口算两位数加一位数（进位）”一课时，笔者出示算式24+6并让学生用小棒摆一摆，算一算。有学生用小棒操作如图3所示。

在该名学生用小棒摆完后，笔者对学生说：“请同桌互相说一说他先算什么，再算什么？”当学生交流结束后，笔者直接出示如图4-1、图4-2所示的小棒图，并对学生说：“不再动手操作，看图说一说计算的结果。”学生回答后，笔者将刚刚解答的三道算式的图示集中呈现，让学生说一说分别是先算什么，再算什么。经历了这样的表达过程，学生的操作、语言表达都转化成了思维，为其思维进阶打下了坚实的基础。

（二）多元性表达：筑思维进阶之基

多元性表达是在丰富和正确的经验性表达基础上，让学生对解决问题的经验进行交流、质疑和反思。这不仅充分让学生表达了自己的想法，还能让学生理解同伴的解题方法。在这个过程中，学生将丰富的经验外化为对解题思路的多元表达，同时在与同伴交流和自我反思中，使自身的表达趋于准确。在课上，教师要让学生充分表达自己的想法和解题思路，尤其要重视课堂小结，鼓励学生进行多元性表达，让学生在对比、思辨、评价、互补中发散思维，这不仅能培养学生的表达能力，还能培养学生总结、归纳和概括的能力。而这，实际上就是学生思维进阶的过程。

让学生在观察、操作等数学活动中丰富经验性表达不是教学目的，它只是学生思维得以展开的手段。学生面对数学问题的经验性表达主要基于自身的学习和生活经验，虽然教师创设了利于学生数学表达的情境并提供了多样的学习材料，但是作为学习个体而言，若学生只能表达出自己的解题思路，则说明其思维结构依旧比较单一。而多元性表达主要来源于与学习共同体的互动交流，学生在互动交流中表达了自己的想法，聆听了同伴的解题思路，接受了同伴的质疑和补充意见。在这个数学表达的对话中，学生完善了自己的思路，学会了接纳同伴的意见。

多元性表达所发挥的教学作用主要有三点：一是让学生集中表达自己对数学知识的学习经验，让自己和同伴具有更加丰富的数学活动经验；二是引导学生整理自己的解题过程，使自己的解题方法更简洁；三是将多种解题方法进行比对和关联，形成启迪性成果，为结构性表达打下基础。可见，多元性表达是学生将经验性表达中隐含的数学思维展露出来的必要过程，更是跨越经验的局限性，实现思维进阶的必经途径。

1.主体多元：拓展数学表达的广度

最基本的学习共同体就是学生所在的小组以及所在的班级。小组和班级是客观存在的集体，如何用好小组和班级学习共同体才是关键。在合作交流之前，教师为学生提供了利于表达的问题和丰富的学习材料，让学生对数学问题形成了自己的见解，但这种见解是有局限性和片面性的。学生只有在小组和班级中进行表达和交流，才能完善对知识的认识，同时收获更多的解题思路。在小组合作和班级交流中，学生通过表达不仅可以整理自己的解题思路，还能从同伴处获得更多的启迪，以丰富、完善解题思路。

例如，在教学“认识负数”一课时，笔者在学生利用情境和学材有了自己对负数的理解之后，便安排学生进行小组交流。

生1：“-1米”，就是将我站的地面看作0米，向下挖1米。

生2：“-1℃”，即比0℃还低1℃的温度。

生3：“-1层”，表示地下1层。

生4：“-1元”，表示用去了1元。

……

这样的交流，使学生对“-1”的理解从单一（个体的经验）到多元（同伴的经验）。学生通过交流，积累了丰富的知识经验，为思维进阶打下了坚实的基础。需要注意的是，小组合作只有建立在学生丰富的经验性表达基础上才能发挥更大的效用。

2.形式多样：挖掘数学表达的深度

数学表达除了不同主体的多元表达，质疑、讨论、释疑、反思等也是学生思维进阶的重要方法。质疑是一种高效的表达方式，学生通过质疑可以了解别人的想法，对比自己的观点，找出彼此观点的相同点和差异之处，并激励自己进行更为深入的思考。在解决问题的过程中，教师不仅要善于提出优质问题，更要鼓励学生大胆质疑，利用问题不断激发学生的思维，让学生在质疑、讨论、表达、释疑的过程中达到深度学习，提升数学表达能力。虽然质疑与反思是多元表达必备的环节，但是学生发表的观点可能是片面的或错的。因此，数学表达不能是“你说我听”，更不能是“你怎么说我也怎么说”，而应该是表达与表达的碰撞、思维与思维的碰撞，促使学生的思维得到更高层次的提升。

质疑、讨论、释疑、反思等都是一种表达能力，教师要在课堂教学中培养学生养成质疑、讨论、释疑、反思的习惯和能力。如在学生发言后让其余学生对难以理解的部分进行质疑，或者鼓励学生对重点处“明知故问”，让学生的思维在质疑和释疑过程中得到进阶。

（三）结构性表达：展思维进阶之翼

所谓结构性表达，是指对数学问题进行多元认识的基础上，依据一定抽象性，经过对比和关联，作出解决问题的基本结构的一种数学交流表达。

结构性表达是学生对数学知识的阐述和解释。学生的数学表达具有结构性，反映出学生的思维已经进阶到“关联结构”水平，是学生思维实现质的跨越的一种表现。