基于单元整合的问题链教学设计与实践

［摘 要］教师应在单元整合的基础上，通过问题驱动学生深入思考，引导学生在解决问题中构建知识、体验思想、积累经验。文章从“三角形”教学内容展开，从教材解读、构建问题链主线、实施问题链教学三个方面探讨“三角形”知识的整合设计与思考，在单元整合视角下研究问题链教学，落实学生深度学习的教学实践与成效。

［关键词］问题链；单元整合；三角形

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）05-0061-03

为了提升学生的数学能力，教师需要全面规划教学活动并进行单元教学。如何确保单元教学能有效提升学生的能力？笔者认为应在单元整合的基础上，通过问题链教学，利用问题驱动学生深入思考，在解决问题中构建知识、体验思想、积累经验，在数学核心思想的脉络化思考中发现并提出问题。基于单元整合的问题链教学回应了培养核心素养的教育价值诉求，并为核心素养的培养提供了现实载体。

基于此，笔者将从“三角形”这一单元展开，从教材解读、构建问题链主线、实施问题链教学这三个方面探讨“三角形”单元整合设计与思考。

一、基于教材解读，指引教学前行路

对教材进行整体分析、明确教学目标及了解学生的学习起点是设计问题链的依据。在设计问题链时，应以单元知识体系、单元目标、学情为指导，梳理知识脉络，并针对具体课型和学习目标加以设计。笔者从钻研教材入手，梳理单元的编排路径，为实现单元整体设计厘清思路，深刻而全面地把握知识之间的联系，从而确定本单元的问题链，以促进学生深度学习。

（一）联系知识体系

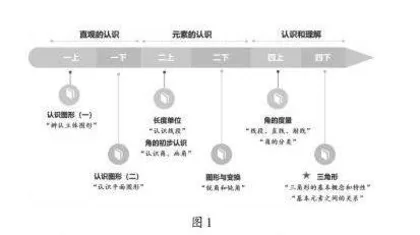
本单元是关于“图形的认识”的课程内容。苏教版教材关于“认识图形”的编排是从图形的直观认识延伸到对图形元素的认识和理解，是从具体到抽象的延伸（如图1）。

分析教材中“三角形”的编排结构，可以发现“三角形”的认识是从学生的认知规律出发，从具体到抽象层层递进。本单元是在直观表象的基础上，深入探索三角形的内部特征，由浅入深。

（二）对比各版本教材的编排

笔者将各版本教材的“三角形”内容进行了梳理，发现各版本教材对“三角形”内容的编排顺序如图2所示。

本文以苏教版教材为例进行分析，通过与人教版、北师大版教材对比，笔者发现它们有相似之处：

1.情境图都是生活中的实际场景，体现了数学源于生活，引导学生体验数学的价值；

2.在“三角形的分类”之后编排“内角和”是必要的。这是因为教学中无法列举所有三角形的内角和，只能通过对不同种类的三角形进行实例验证；

3.在例题中，安排了如画、量等活动，这些都体现了教学过程中对学生动手操作和观察分析的重视。

二、基于单元整合，构建问题链主线

本文基于单元整合的问题链教学研究，通过问题链中的各个问题来培养学生的多元化思维方式。

（一）关注要素：边和角

在探讨三角形时，边和角是两个不可或缺的要素。教师可以通过问题链（见表1）引导学生深入探究边与角之间的关系，以及这些关系如何影响三角形的形状和性质。

（二）关注要素：边

在专注于“边”这一要素时，教师可以通过问题链引导学生探究三角形的三边关系、稳定性及边长变化对三角形的影响（见表2）。

（三）关注要素：角

在探究“角”这一要素时，问题链的设计应围绕三角形的内角和，及其与多边形的内角和的关系展开（见表3）。

三、基于深度学习，践行问题链教学

问题链教学旨在借助问题来设置学习任务，并利用“链”来构建数学思维的路径。问题链教学能够给予学生数学思考的环境和路径，促进学生深度学习，实现思维进阶，培养学生的数学核心素养。

（一）关联：建立认知结构，促进知识关联

在本单元的教学中，笔者将本单元的知识进行关联，引导学生从三角形的边、角、顶点三元素研究，建立认知结构，为学生建立认识三角形的基本框架，促进知识关联。以“三角形的认识”教学为例，以“画三角形”的问题链关联三角形与已有经验，感知三角形三要素的关联，感悟高与三角形的关联。

问题1：你是怎么画三角形的？

问题2：画有一条边为10厘米的三角形，每个人画出的三角形都一样吗？

问题3：画底为10厘米，高为8厘米的三角形，每个人画出的三角形都一样吗？

展示验证：顶点和高的位置不同，三角形的形状也不同（如图3）。

本节课是单元重构后的起始课，在知识关联的基础上，笔者设置了“画三角形”的问题链，旨在将学生的已有经验转换成抽象知识，结合方法关联、视角关联等聚焦在问题解决上，从而实现新旧知识的链接，打通知识脉络，使学生获得系统的知识和经验。

（二）表征：促进知识理解，渗透多元表征

在本单元“三角形的稳定性”的教学过程中，始终贯穿体验表征、图形表征、逻辑表征等方法，同时，通过语言表征让学生感受到三角形的稳定性。本节课交叉运用图形表征、操作表征、逻辑表征（如图4），激活学生内心体验的同时，让学生从本质上构建新知识。

教学中可以设计如下问题链。

问题1：三角形具有稳定性吗？（从同样长的7根小棒任选几根搭任意平面图形）

问题2：给你3根不同的小棒拼三角形，拼出的三角形会不会一样？

问题链教学倡导用问题促进学生主动参与，驱动学生进行思考。因此，在问题链教学时应渗透多元表征来促进学生对知识的理解，并强调学生的主体地位。教师将教学内容以问题链的形式出示，可以有效杜绝“满堂灌”的现象，问题与表征的结合必激发学生思考，产生内在认知需求。

（三）进阶：引发深度思考，实现思维进阶

“三角形的稳定性”一课，不应停留在“三角形稳定”这一性质上，而应通过问题链层层递进，让学生思考如何让四边形不再变形，再让学生通过操作体验如何让架子更具稳定性，一步一步促进学生思考，实现思维进阶。

问题1：这样搭成的架子具有稳定性吗？（如图5-1）

问题2：怎样让架子更具稳定性？（学生拼搭如图5-2所示）

本节课依托问题链让学生在操作中直观体会三角形的稳定性，从而掌握三角形的本质属性。

总之，在单元整合的问题链教学中，问题由浅入深、由具体到抽象、由抽象到生活，引发学生深度思考，学生在深刻理解知识的基础上抓住内在联系，构建知识体系，从而真正理解知识，实现深度学习。

［ 参 考 文 献 ］

[1] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[2] 唐恒钧，张维忠.数学问题链教学的理论与实践[M].上海：华东师范大学出版社，2021.

（责编    黄    露）