基于前测的小学数学概念精准教学实践与思考

［摘 要］“平均数”是小学数学中非常重要的概念，平均数的抽象性、统计性与四年级学生思维的形象性形成矛盾，因此通过前测把握学情，重构生本课堂是很有必要的。文章以“平均数”教学为例，从前测思考、学情把脉、课堂重构三个方面浅谈对小学数学概念精准教学的实践与思考。

［关键词］平均数；概念教学；前测

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）05-0064-03

有效的数学学习活动不能单纯地依赖模仿与记忆，动手实践与合作交流是学生学习数学的重要方式。在概念教学的过程中，教师要充分发挥主导作用和学生的主体作用，让学生参与分析、比较、抽象、概括等一系列思维活动过程，以此加深对概念的理解。

“平均数”是小学数学中非常重要的概念，对于以形象思维为主的四年级学生而言，平均数的抽象性和统计性是很大的一个挑战。如何把握学生的学习起点？前测就是一种行之有效的方法。通过前测，教师可以了解学情，确定教学重难点，从而构建生本课堂。下面，笔者以“平均数”教学为例，从前测思考、学情把脉、课堂重构三个方面浅谈对小学数学概念精准教学的实践与思考。

一、以教材为基铺前路

教材是教学设计的“原材料”，研读教材是教学的立足之本。数学前测要研究的是“具体儿童”，关注的是儿童的动态成长。为了做出更有检测意义的前测卷，第一步就是研读教材，吃透教材。

人教版小学数学实验版教材把“平均数”安排在三年级下册，教材改版后，这一内容被调整到四年级下册，且例题的情境也有了变化。例1呈现的不同之处在于前者根据直观图引出“移多补少”法，同时得出用求和均分的方法，没有直接引出“平均数”这一概念；修订版教材明确提出了“平均数”这一概念，从算法理解走向意义理解。例2中的素材，两队的人数由相同变成不同，通过“两队人数不同，不能用总数比较”这一思维的矛盾，让学生经历交流、争辩、分析与比较的过程，使学生进一步理解平均数的意义，进而发现用平均数进行比较的合理性，体会平均数在统计学中的意义。此外，教学用书也发生了改变，由“使学生理解平均数的含义，初步学会简单的求平均数的方法，理解平均数在统计学中的意义”变成“体会平均数的作用，能计算平均数，能用自己的语言解释其意义”，强化学生对平均数含义的理解，感悟其在统计学上的作用。

基于教材对“平均数”这一内容的改编，笔者在设计前测题的时候考虑到以下因素：一是全面了解学生的知识储备、经验储备、能力储备等；二是还原学生的思维过程；三是呈现学生之间的能力差异。因此设计了三道前测题：

题1.你在生活中见过平均数吗？都是在哪看见的？（旨在了解学生的生活经验）

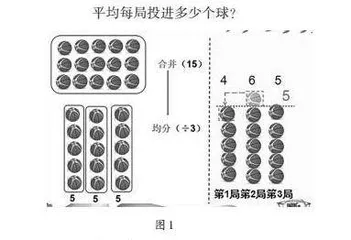
题2.小强在进行投球训练，共进行3局，第一局，他投进4个球；第二局，他投进6个球；第三局，他投进5个球，他平均每局投进多少个球？（旨在了解学生对平均数的算法的掌握情况）

题3.一匹小马高1.6米，一条河的平均深度是1.5米，小马能安全过河吗？（旨在了解学生对“平均数代表统计对象的一般水平”的理解程度）

二、以前测为眼识学情

前测是数学课堂的“眼”，是教学的依据，能够把准学情之脉搏。通过对前测结果的分析，笔者探寻到“平均数”教学的起点，了解到真实学情，以此定位本节课的教学重点。

本次有效前测卷40份，笔者经整理分析发现，在第1题中，60%的学生虽然听说过平均数，但是很少能举出具体的例子，说明这部分学生的生活经验不足；在第2题中，学生基本会用“合并均分”的方法计算出平均数，另有32.5%的学生会用“移多补少”法，说明平均数的计算方法对于学生来说是相对容易的；在第3题中，67.5%的学生认为小马不能安全过河，其中只有7.5%的学生的理由是正确的，这说明大部分学生并不能准确理解平均数的意义。

从前测中笔者还发现学生知识水平的差异还是很大的，有部分学生已经知道了平均数的特征，而有些学生却没听说过。因此，笔者将本节课的重点定为“在学生熟悉的生活情境中构建平均数的概念，理解平均数的意义”。

三、以学情为鉴塑课堂

前测是为了了解学情，以学情指导教学。以学情为鉴，如何选择教学情境、设计教学活动，扎扎实实为学生的“学”服务，还学生一个“生本课堂”呢？笔者认为不妨从以下三个方面入手。

（一）甄选素材，生活寻趣映智慧

从对前测结果的分析来看，学生关于平均数的生活经验较少。那么，教学这节课应选择适合学生、贴近学生、让学生感兴趣的材料。

例如，本节课引入“投篮挑战赛”这一情境，在这一情境中探究平均数的意义、算法、特征。

有效的情境是有趣的、能调动学生学习热情的、能引发学生思考的。这节课所有的素材都是源自学生的实际生活，学生在真实的情境中探索平均数的算法、领悟平均数的意义、感知平均数的特征，从而实现思维的升华。

（二）攻克难关，细微之处见亮点

1.数形结合，促概念构建

“数缺形时少直观，形少数时难入微。数形结合百般好，隔离分家万事休。”华罗庚先生在《谈谈与蜂房结构有关的数学问题》中说明了数形结合思想的价值。“形”的最大优势是直观形象，“数”则准确抽象。“数”和“形”结合起来，就将准确而抽象的“数”形象化了，从而呈现出其中的内涵。数形结合是一种比较适合小学生的思维方式。

“平均数”是通过“合并均分”或“移多补少”得到的，是一个比较抽象的概念。因此笔者在教学过程中将两种方法通过课件（如图1）直观展示，沟通平均数的求法。

平均每局投进多少个球？

2.选题审慎，求科学严谨

前测的第3题中，学生在说明小马不能安全过河的理由时，52.5%的学生给出的理由都是与题目无关的，如水可能会淹没到小马的眼睛。笔者分析出现这种情况的原因，一是学生的知识储备不足，二是题目自身存在一定的问题。因此，在概念教学时，教师选取的题目一定要力求科学严谨。

练习题避免存在强行编造、似是而非的问题。水深问题（如图2）在很多平均数教学设计中都会用到，仔细考量后不难发现这类题目有一种似是而非的感觉。如“平均水深1.1米，严禁下河游泳”，日常生活中很少出现这种的警示标语，真正的标语是“水深危险，严禁游泳”。另外，用一个截面的五处水深来解释一个三维不规则曲面深度的平均值，本就是一种缺乏实际意义的做法。类似这些不够严谨的题目，教师在选择时应该尽量避免。教师精心选题，尽可能展示学生的思维误区，尽可能追求科学严谨，做到符合学生的认知规律，这有助于学生构建、理解、掌握平均数的基本概念。

（三）生本为魂，课堂之上共乐融

学生是数学学习的主体，教师是数学学习的组织者、引导者、合作者。教师应选用学生感兴趣的素材，引发学生的积极性，以期让学生发散思维。

以“年龄问题”教学为例。

教师出示任务：有4个人，他们的平均年龄是10岁，他们的年龄分别可能是几岁？（有多种组合）

师：1分钟倒计时，比一比看谁写得多。

（1分钟倒计时）

师：你们写了几组？

生1：4组。

生2：7组。

生3：8组。

生4：10组。

师：你有什么窍门能在1分钟里写了这么多？

生5：只要4个人的年龄和是40，他们的平均年龄就是10岁。

师：你也太厉害了，为你点赞！

课后回收学生的39份练习纸，笔者发现学生给出的答案各不相同，最少的写出了3组，最多的写出了10组（如图3为部分学生的答案），如果时间足够估计写得更多。不同的学生写的数据不一定相同，但是平均数都是10，说明学生已经不自觉地参与到平均数特征的探究中。学生写出的数据比笔者预期的要丰富，他们还考虑到了特殊组合，如10，10，10，10；0，0，0，40。甚至在写数据的过程中，学生还体现了有序性，如从0开始思考，数据逐渐增大，从而写出多组符合题意的数据。学生写出这么多数据，自然能感知到平均数不能代表某一个体的具体情况，而是反映一个群体的一般情况。由此可见，在这堂课上，学生充分发挥想象力，愿意表达自己的想法，也有内容可分享，真正成为课堂的主人。不同学生为这节课提交了不同的答卷，收获了快乐。这是一节充满活力、富有张力的数学课。

基于教材，精准设计前测题目；基于前测，把脉课堂；基于学情，重构生本课堂，抽象难懂的概念课也可以变得“近人情”，课堂也可以变得富有张力、生命力和活力。学生在“趣”中构建概念，升华思维，用细节点亮课堂，并乐在其中。

［ 参 考 文 献 ］

[1] 徐彩霞.架生活之桥   展课堂之彩[J].新课程学习（上），2011（6）：111-112.

[2] 史晓燕，沈百军.找准起点   建构新知：“平均分”教学实践与反思[J].教学月刊小学版（数学），2013（12）：7-10.

[3] 史宁中，曹一鸣.义务教育数学课程标准（2022年版）解读[M].北京：北京师范大学出版社，2022.

（责编    黄    露）