融入数学文化促进学力生长

［摘 要］数学文化教育是数学教育的重要组成部分，苏教版教材“你知道吗”板块为数学文化教育提供了平台。文章以“多边形面积”单元中的“你知道吗”板块为研究蓝本，以“古今数学之旅”这一主题情境设计作业，引导学生走进图形测量的历史，沿着古人的足迹感受“以盈补虚”的数学文化理念，体会转化思想的魅力，为学生后续的图形与几何学习打下基础，从而实现数学学科的育人价值。

［关键词］数学文化；多边形面积；“你知道吗”板块

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）05-0070-03

数学教材中的文化素材丰富多样，小学数学教材的好几个版本都设置了“你知道吗”板块来介绍数学文化。除了通过课堂教学和综合实践活动等途径，教师还应在作业设计中融入数学文化，帮助学生了解数学文化，激发他们探究数学文化的热情，领悟数学思想方法，进而发展数学核心素养。

一、数学文化教育的意义和价值

《义务教育数学课程标准（2022年版）》指出，数学承载着思想和文化，是人类文明的重要组成部分；关注数学学科发展前沿与数学文化，继承和弘扬中华优秀传统文化。这表明，数学不仅是一门学科，也是一种文化，数学文化应作为一项重要内容融入数学课程中。

数学文化的渗透不仅帮助学生理解数学知识，还能让他们了解数学历史的发展进程，感受数学思想的魅力，提高对数学的兴趣。数学文化中的演绎论证有助于培养学生的理性思维，使他们会用数学的眼光观察世界，会用数学的思维思考世界，会用数学的语言表达世界。

二、“你知道吗”板块是数学文化教育的“重要阵地”

苏教版教材的“你知道吗”板块涵盖“数学史”“数学知识介绍”“生活中的数学”和“生活常识与信息”等内容，旨在帮助学生了解人类数学发展史及我国传统数学历史，激发学生的民族自豪感，使得学生感受数学与生活的关系，领悟数学思想方法，发展数学思维品质。

教师应加强对数学文化知识的学习，积极挖掘数学文化素材，充分利用“你知道吗”板块中的内容，将这一板块融入数学课堂的综合实践活动中，也可以将其整合进作业设计中，推动数学文化的全面融入与落实。

三、依托“你知道吗”板块在作业中融入数学文化的策略

苏教版教材“多边形面积”单元中的“你知道吗”板块介绍了《九章算术》中的“半广以乘正从”方法，并通过“以盈补虚”法加以说明，让学生感受古代数学文化思想，进一步理解转化思想在面积推导中的作用。

笔者以该素材为例，探讨将数学文化融入作业设计的策略。作业设计以“古今数学之旅”为情境，分为六个旅行站点“考古小镇、古回来廊、刘徽再现、解密赛场、创意测算、智慧空间”（如图1），通过综合运用数学、语文等学科知识与生活经验，引导学生一边探寻图形面积计算的历史起源，一边感受数学文化的博大精深。

（一）考古小镇——阅读图“绘”，品味文化魅力

古代数学文化博大精深。在此站，学生将“穿越”时空，阅读史料，了解古代数学家及其经典著作。

【活动1】对话古人，我有话说。刘徽的著作《九章算术》对后世影响极大。阅读相关材料，并用自己的话介绍《九章算术》。

【设计思考】通过阅读有关《九章算术》的材料，学生将了解古代数学家及其数学著作，感受数学家的思想和精神，感受中华数学文化的悠久历史。

【活动2】东汉末至三国时期的赵爽为《周髀算经》作序时，绘制了一幅“勾股圆方图”，后世称这个图为“赵爽弦图”。弦图之美，美在简约，然不失深厚，经典而久远，被誉为“中国数学界的图腾”。2002年北京国际数学家大会依据“赵爽弦图”制作了会标。请尝试绘制“赵爽弦图”，体会其美感。

【设计思考】通过绘制弦图，学生在浓厚的数学文化氛围中感受图形之美，与传统数学文化“牵手”。

【活动3】温故知新，我有理推。“几何之父”——古希腊数学家欧几里得的著作是《几何原本》。请查阅资料，了解欧几里得是如何推理得出“三角形内角和是180度”定理，将其与已学过的方法进行比较，尝试用欧几里得的方法推理四边形内角和。

【设计思考】通过阅读史料，学生可以了解国外古代数学家的数学思想，并通过讨论和记录，深化对古代数学方法的理解。

（二）古今回廊——古今对照，感悟数学思想

了解古代国内外的三角形知识后，学生将追溯古代三角形面积的计算方法，进一步提升对数学的兴趣，提升推理与归纳总结能力，感悟转化思想的作用，积累数学活动经验，为后续推导更多平面图形的面积做铺垫。

【活动4】走进《九章算术》。让我们穿越回古代，再次领略古代数学家的风采。请阅读课本中的“你知道吗”内容，用“以盈补虚”的方法来推导三角形的面积公式，可以画一画、折一折。如果觉得困难，可以先从直角三角形的面积入手，再考虑锐角三角形和钝角三角形的面积，最后归纳三角形的面积公式。

【设计思考】通过自主探究，学生将领略古代数学文化思想，并在多元表达中提升逻辑推理与归纳总结能力。

【活动5】再忆课本。回忆教材是怎么引导我们探究三角形的面积的？请讲解。

【设计思考】从古代“以盈补虚”法推导三角形面积回归教材的拼合法推导三角形面积，学生体会到古今数学思想方法的相通点，感受解题方法的多元化。

【活动6】方法讨论。“以盈补虚”法和拼合法有什么共同点和不同点？可以录制解说视频，也可以写数学小论文来进行说明。

【设计思考】通过讨论与表达，学生将加深对三角形面积推导方法的理解，提升思维的深度与广度。

（三）刘徽再现——挖掘本质，培养严谨思维

在探究三角形面积的基础上，引导学生从多角度、多层次自主探索梯形的面积公式，利用知识的迁移完善学生的整体认知结构。

【活动7】我“形”我算。请大家当一回“刘徽”，发挥聪明才智，通过折一折、算一算推导梯形的面积公式。

【设计思考】通过类比迁移，从三角形面积公式的推导延伸到梯形的面积公式推导，在“转化”这个核心方法的基础上进行延伸，进一步提升学生的推理能力。

【活动8】贯通古今。《九章算术》中提到“邪田（直角梯形）”的面积计算方法——“并两广若袤而半之，以乘正从若广。又可半正从若广，以乘并”和“箕田（等腰梯形）”面积的计算方法——“并踵舌而半之，以乘从”，也就是我们所说的“上底加下底的和乘高除以2”。著名数学家刘徽对此用“以盈补虚”法加以说明。看完你有什么感受，收获了什么？可以用视频的形式或手账的形式表达。

【设计思考】学生在自主探究后阅读《九章算术》的相关内容，领略数学思想在发展的过程中所迸发的魅力。

【活动9】联系发现。长方形、平行四边形、三角形、梯形的面积计算方法有什么联系？

【设计思考】通过对不同图形面积计算方法的总结，学生将加深对数学方法一致性的认识，提升归纳总结能力。作业形式可以多种多样，如海报、PPT、研究报告等，多方面发展学生的综合能力。

（四）解密赛场——分层拓展，发现数学之趣

在解密赛场，学生将运用前几站积累的知识，挑战更复杂的问题。

【活动10】

题1.三角形农田（必做题）。今有圭田（等腰三角形）广十二步，正从二十一步，问田为几何？

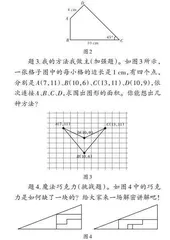
题2.寻找三角形（必做题）。如图2所示，四边形的BC=10 cm，AD=4 cm，求四边形的面积。

题3.我的方法我做主（加强题）。如图3所示，一张格子图中的每小格的边长是1 cm，有四个点，分别是A（7，11）、B（10，6）、C（13，11）、D（10，9），依次连接A、B、C、D，求围出图形的面积。你能想出几种方法？

【设计思考】围绕“图形的面积计算”设计了必做题、加强题和挑战题，学生可根据自身学习进度合理选择。这些题目既能帮助学生巩固面积计算方法，夯实知识和技能，又能激励学有余力的学生逐步突破。第1题以文言文形式呈现，结合“半广以乘正从”这一知识点，融入传统数学文化；第2题通过添补三角形，展示面积计算的灵活运用；第3题利用坐标点构造图形，结合割补法和格子数估算，融合面积估算与精确计算；第4题通过与图形拼搭相结合，既具趣味性，又充满挑战性，引导学生用数学眼光观察和分析图形，用数学语言揭示“魔法”的奥秘。

（五）创意测算——数学实践，体会探究之乐

通过创意测算，学生将体验图形面积计算在生活中的实际应用。

【活动11】惠丰商业广场的工作人员想算一算商场周边这片区域的面积，请大家帮帮忙！

提示1.可3～5人组队后分工合作，设计一种方法进行测算，有创新方法更好。可用地图测量计算的方法、参照物法测量计算（以周边一个已知面积的小区或其他规则区域为参照物进行估算）……

提示2.需要提供主题活动设计方案、活动图片、活动结果。

【设计思考】学生通过动手实践和分工合作，逐步发现多边形之间的内在联系，体会到多边形面积计算的一般策略。在实际操作中，他们不仅能够深化对已学知识的理解，还能在探索过程中不断获得新认识，发现并提出有价值的数学问题，从而发展问题意识。

（六）智慧空间——拓展延伸，传承数学文化

作业设计在时间和空间维度上贯通古今中外，拓展学生的数学视野。

【活动12】勒洛三角形是由德国科学家勒洛首先发现。想知道勒洛三角形是怎么画出来的吗？请查阅资料后自己动手绘制勒洛三角形，并讲解你的方法。

【活动13】勒洛三角形有什么特征？在日常生活中又有哪些应用呢？请自主查阅资料，探寻勒洛三角形的秘密。

【设计思考】勒洛三角形的绘制过程涉及尺规作图的相关知识。通过读、画、写、说等活动，提升学生的自主学习、动手操作、语言表达等能力，鼓励学生持续探究数学文化。

总之，依托“你知道吗”板块设计创新作业，不但能够帮助学生深入了解数学思想的本质，促进教师提高对数学文化的洞察力和理解，改善教学观念，还能鼓励学生自主探究，提升学习的有效性与个性化表现，促进学生的学力生长。

［ 参 考 文 献 ］

[1] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[2] 张定强，王金燕.“数学文化”研究20年：成果与展望[J].江苏教育研究.2022（7）：81-86.

【本文系江苏苏州市教育科学“十四五”规划立项课题“数学基本思想视角下小学数学学科育人价值的研究”（课题编号：2021/LX/02/380/10）阶段性研究成果之一。】

（责编    黄    露）