以“支架式”教学落实学生自主探究能力的培养

［摘 要］“支架式”教学是指利用学生最近发展区，引导学生搭建结构性知识、关联性知识、整体性知识等支架，促使学生探究；搭建图形、操作、审辩等方法支架，提升探究效能。并通过三步支架程序让学生自主构建支架，从而提升自主探究能力。

［关键词］“支架式”教学；知识结构；自主探究

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）05-0085-03

《义务教育数学课程标准（2022年版）》提出，教学活动应注重启发式，激发学生学习兴趣，引发学生积极思考，鼓励学生质疑问难。笔者认为数学教学活动应为学生搭建学习支架，挖掘学生学习生长力，引发学生积极思考，并促进学生自主探究。因此，笔者在教学过程中，利用学生最近发展区，搭建“脚手架”，引导、鼓励学生在学习中努力探索，借助或自主构建支架，从而独立探究学习。

一、构建知识支架，促进有效探究

（一）借结构性知识支架，体验知识纵向发展探究路径

结构性知识支架是运用学生的认识结构和数学知识结构构建的支架，运用结构性知识支架可进行独立的探索活动。

【教学案例1】

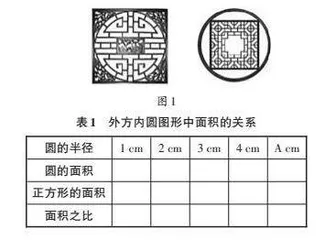
在人教版教材六年级上册中，有内容“外方内圆和外圆内方”，指出中国传统建筑中常见到这两种设计（如图1）。学生已对圆和方有了认识，笔者利用这个结构性知识支架设计例题（见表1），学生探究出外方内圆图形中圆的面积与正方形的面积之比是[π]∶4。

【设计意图】在这样的结构性知识支架中，学生能够自主探索出外方内圆图形中圆的面积与正方形的面积之比是[π]∶4。同样，探究外圆内方图形对学生而言也不是一件困难的事情，学生能够得出正方形的面积与圆的面积之比是2∶[π]。因此，从例题中支起结构性知识支架，到撤去支架，自主构建支架进行探究，学生的知识体系将从实际发展区逐步过渡至潜在发展区。当然，撤支架与自主构建支架的过程会有交叉融合，这将促进学生更深入地进行自主探究，同时使知识构建过程更加具有结构性。

（二）借关联性知识支架，经历知识横向发展探究路径

学生的知识建构是逐步从一课、一个知识点走向一个单元的知识点、几个单元知识点，甚至是整册或数册的知识架构的。因此，以情境关联知识点，利用知识点的“关联建构”是实现从“单个概念认知”走向“关联概念架构”的必要支架，也是形成对知识的自主探究，并在“知识结构化”的过程中促进知识建构能力的提升和对概念的深度理解的支架。

【教学案例2】

以人教版教材三年级下册“除数是一位数的除法”单元教学为例，当讲到“两位数除以一位数”的内容（如图3）时，教师应以情境关联算理，提供实物支架让学生清晰地记录每一次分小正方体的过程以及结果，从情境中探究每个数的意义。

【教学案例3】

在教学人教版教材五年级上册“小数除法”单元的“一个数除以小数”的内容时，教师应横向关联算理。出示问题：奶奶编中国结，编一个要用0.45米丝线，这里有6.75米丝线。这些丝线可以编几个中国结？

【设计意图】虽然所探讨的这两个问题一个是三年级整数除法，一个是五年级小数除法，但在学生探究这两个问题时，情境支架体现知识的横向联系，帮助学生理解算理。因此，让学生感悟这样横向发展的关联性知识支架，能够促进他们更好地自主构建支架、自主探究小学阶段的整数、小数的计算，进而拓展到新的领域。在这个学习过程中，学生的探究能力也得到了提升。

（三）借整体性知识支架，感悟知识整体发展探究路径

在学生整体建构知识体系的过程中，以单元知识构建整体性知识支架，确保学生对单元的整体知识进行深入思考。学生可以将整个单元的知识点呈现在“单元知识”的思维导图上，不遗漏，同时建立知识点间的联系，形成单元知识的“全景图”。

【教学案例4】

出示问题：我们学习了关于长方体和正方体的很多知识，主要包括长方体和正方体的认识、表面积的计算、体积单位、体积的计算等。这些知识是存在内在联系的，请用思维导图整理它们的内在联系。

【设计意图】教师提供一些长方体、正方体单元知识支架，让学生进行自主梳理，自主构建支架、自主探究单元知识点的联系、重点、难点。这一过程不仅有助于学生将所学知识系统化、结构化，还能让他们感悟知识整体发展探究路径。整体性知识支架对小学数学单元复习教学的变革有促进作用，也是提升学生自主梳理、自主探究能力的一种有效方式。

学生知识发展与自主探究能力的提升并非仅限于单一维度或线性发展，而是一个面或是一个整体。因此，在课堂的实践中，结构性知识支架、关联性知识支架、整体性知识支架可以单独使用，也可以混合使用，但不论如何使用，过程都遵循“帮助学生构建支架—撤去支架—学生自主构建支架”的教学路径，最终实现自主探究的目标。

二、构建方法支架，多元探究显效能

（一）图形支架破难点

搭建图形支架，让思维过程可视化。

【教学案例5】

在教学人教版教材三年级下册“万以内的加法和减法（二）”单元时，课堂教学中发现在计算403-198时，学生采用了两种计算方法，方法1是403-200-2，方法2是403-200+2，学生对两种方法产生了争议。部分学生提出通过直接计算来验证答案，得方法2正确，但对于方法1为什么是错的，学生仍感到困惑。笔者在课堂提供图形支架，让学生尝试画图理解，学生清晰地从图中看到错误之处。

【设计意图】通过提供图形支架让处于困惑中的学生能够理解原因，同时指向教学的核心，促进学生的思维发展。撤去支架，让学生遇到相似困惑点或是难点时自主构建图形支架，自主探究类似的问题，从而提升学生的探究能力。

（二）操作支架促理解

在学生刚接触新知识时，学习材料非常重要，因此，教师需要搭建操作支架，以深化学生对概念的理解，并帮助学生实现对数学知识、数学思维的自我建构和发展，使得后续学习更有力。

【教学案例6】

在教学人教版教材三年级上册“长方形和正方形”单元时，学生刚开始学习面积的计算，为此，笔者提供了边长1厘米，面积1平方厘米的正方形，再给出一个长方形图形，让学生用1平方厘米的小正方形摆一摆，并估测长方形面积，最后记录结果。学生自主操作后有几种摆法：方法1是铺满格，方法2是铺行与列，方法3是用正方形边长去对比长方形的长和宽，方法4是直接测量长和宽。之后，笔者组织学生讨论哪种方法更为高效和准确。

【设计意图】本次活动具有承前启后之效，学生在学习面积单位时，已经会用1平方厘米的正方形直接测量并估计待测平面图形的面积。教师鉴于学生已有认知结构提供感悟面积的操作支架，唤醒学生已有的学习活动经验，让学生直观地感知每行个数、行数与单位面积数的联系。慢慢撤出支架，学生有能力自主构“架”、自主探究完成正方形的面积度量操作。

（三）审辩支架展质疑

数学的魅力在于思维的挑战，特别是思维冲突中获得的成功，而提供审辩支架是促进学生数学主动探究的一种重要的形式，审辩中展示出思维的质疑之处、冲突之处，这对完善个人思维模式是一种有效手段，也是提升学生自主探究能力的关键途径。以知识点进行问题变式，搭建审辩支架，能推动学生改变学习方式，从而提升学生数学反思、质疑、表达能力。

【教学案例7】

在学生学习长方体的体积后，以h=V÷S进行问题变式，问题如下。

王师傅在长方体水箱（如图4）中装了1.2立方米的水，小林说：“水箱中水深为0.1米。”小芳说：“水箱中水深为0.2米。”小李说：“水箱中水深为0.15米。”他们三人争论了很久，你认为谁说对了呢？请用文字或算式说明你的观点。

【设计意图】教师给学生一个审辩支架，提供疑惑点后，学生独立思考、探究，然后展示、汇报己方观点，听取他人观点并提出自己的看法，这是一个共同交流、探讨的过程，在此过程中，培养学生反思、质疑、表达的能力。

课堂中也可能会有新的问题生成，比如“如果不同底面的水面高度一样，它们的体积之间又会有怎样的关系？与底面积又会有怎样的联系？”等问题，学生自主构建支架与自主探究这些新的问题，自主探究能力得到真正发展。

三、三步支架程序，初显探究模型

在教学活动中，教师提供的支架程序会进行不断地变化，学生、教学重点和课堂教学三个方面信息都可能导致整个支架的变动，而且每一种变化都需要教师做出相应的教学决策，采取不同的响应方式，这样，三步支架程序（如图5）是有活力的、有机的、灵活的。

（一）支“架”

围绕学生学习的主题，按照学生已有的知识基础和知识经验，设计知识联结点，用画图、操作、情境、列表、问题串等手段支起支架。

（二）撤“架”与构“架”

在新的知识体系中，学生从不知如何思考到借助教师提供的图形、情境、列表、问题串等支架进行学习，撤去支架后，学生遇到新问题同样能够自主构建新的方法支架和知识支架。教学实践中，从撤“架”到构“架”的过程没有具体的分界，视学生的掌握情况而定，如果学生的掌握水平较高，则可以在合适的时候撤“架”或构“架”，也视具体情况决定是单独进行还是交叉进行。

（三）独立探究与合作学习

在自主构“架”后，学生在独立探究与合作学习的过程中，充分运用方法支架和知识支架，展示自我、突破难点，走向另一个新的知识区域。

在教学中，知识支架和方法支架可以独立运用，也可以几个支架混合使用。不论是知识支架还是方法支架的构建，始终以学生已有的知识水平为起点，教师搭建支架与学生攀爬支架可以并行也可以交叉，学生可以独立探究也可以合作学习，通过逐步自主构建探究，走向潜在发展区、新的发展区。

［ 参 考 文 献 ］

[1] 特里·汤普森.支架式教学：培养学生独立学习能力[M].重庆：西南师范大学出版社，2019.

[2] 洪树兰.数学“支架式教学”研究[D].昆明：云南师范大学，2006.

[3] 李加树.数学结构化教学漫谈[J].教学月刊小学版（数学），2020（5）：40-43.

[4] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

（责编    杨偲培）