关联：促进学习迁移的小学数学教学实践

［摘 要］学习迁移是指将已掌握的知识和技能应用于新的学习情境。数学具有紧密性、连续性的特点，对学生迁移能力的培养尤为重要。文章通过解析学习迁移理论架构，探讨在小学数学实践中促进学习迁移的策略，以期提升教学质量。

［关键词］学习迁移；关联；教学策略

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）05-0094-03

在数学领域，知识点、技能与解题方法之间存在着紧密的内在联系。这种关联性不仅构成了数学学科的独特魅力，也为学生提供了丰富的学习迁移机会。小学数学的学习迁移不仅仅是简单的知识迁移，还是对学生思维能力的深度训练和拓展。教师应引导学生将所学的数学知识、技能与实际问题进行关联，实现知识的有效迁移，从而提升学生的学习效率，增强他们解决问题的能力。

一、解析学习迁移理论架构的内容关联

美国心理学家奥苏伯尔认为，学习迁移是一种学习对另一种学习相互作用的体现。这种相互作用具有双重性，它既可以产生正向效应，推动学习效果的显著提升；也可能呈现负面倾向，对学习成果造成不良影响。对于小学的数学学习而言，学习迁移指的是学生先前建立的数学知识体系、掌握的数学技能、形成的数学思维，以及积累的解题策略对其后续学习内容所产生的深远影响。这种影响是相互的，即新的数学知识、技能、思想和方法也能够反过来影响和加深对已有知识的理解。

（一）正迁移与负迁移

一种学习过程对另一种学习过程产生正向作用，这种现象被称作正迁移。例如，学生在掌握了“九加几”的加法原理后，学习“八加几”和“七加几”的加法时，便能够将之前学到的“凑十”技巧应用到新知识的学习中，从而加深对新知识的理解和掌握。相对而言，负迁移是指一种学习过程对另一种学习过程产生不利效果。比如，学生在掌握了2和5的倍数特征后，容易陷入一个误区，即知识的过度泛化。他们可能会错误地将这些特征应用到3的倍数上，出现误导性的迁移。

（二）顺向迁移与逆向迁移

根据迁移发生的方向来划分，学习迁移可以分为顺向迁移与逆向迁移。其中，先前学习对后续学习产生的积极影响为顺向迁移。比如，学生熟练掌握“三位数乘一位数的乘法”技巧后，在进一步学习“三位数乘两位数的乘法”时，便能自然地将先前掌握的计算技巧应用到更为复杂的情境中，进而提高学习效率。相对地，在学习的进程中，后续的学习对先前的知识产生影响，被称作逆向迁移。

（三）水平迁移与垂直迁移

在学习过程中，当两项学习活动处于同等的抽象与概括层级时，它们之间的相互作用被归类为水平迁移。这种迁移类型涉及的学习内容在逻辑架构上呈平行关系。与水平迁移不同，垂直迁移则描述了处于不同抽象与概括层级的学习活动间的相互影响。这种迁移既可以是自上而下的高层次抽象概念影响低层次具体概念，也可以是自下而上的具体经验升华至一般原理。例如，在探讨三角形的学习中，学生对“三角形”这一基础性概念的认知将对其后续掌握直角三角形、锐角三角形、钝角三角形等细分类型产生深远影响。

（四）一般迁移与特殊迁移

在学习过程中，将在某一学习领域获得的通用方法和策略拓展至其他多样化的学习范畴称为一般迁移。相对的，将特定学习方法或独特经验直接应用于另一领域的学习称为特殊迁移。心理学家布鲁纳认为基本原理和基本态度因其广泛的适用性，能够在结构上类似但表面差异显著的情境中灵活应用，进而促进后续学习的流畅性和高效性。

通过对上述迁移类型进行细致的分析，可以明确地识别出这四种迁移类型之间的主要差异及其相互关联。这些迁移类型在小学数学教学实践中具有实际应用价值，教师应掌握这些迁移类型的特点，以便更有效地指导学生的学习进程，促进学生实现高效的学习迁移。

二、理解学习迁移概念建构的思想关联

（一）恰当呈现教材，建立认知结构

在学习的进程中，学生根据自身的认知水平，将数学知识进行有序的梳理和整合，从而形成独具特色的数学认知体系。相关研究表明，精心设计数学教材结构，对于提升学生的数学学习迁移能力至关重要。这种高效的教材结构通常采用逐步深化的构建方式：首先引入普遍性强、基础扎实的数学概念，随后逐步深化至更为细致、具体的领域。比如，在教学“三角形”的相关内容时，教师可以根据教材中教学内容的编排顺序进行教学，先是引导学生理解并掌握三角形的基本特征和属性，再逐步引导学生从定义区分锐角三角形、直角三角形、钝角三角形，最后进一步深化至等边三角形、等腰三角形特征的学习。

（二）寻找共同要素，搭建迁移桥梁

在实际教学中，要实现学生学习正迁移，关键在于引导他们如何有效运用既有知识，并洞察新旧知识间的内在联系。这种内在联系如同桥梁，使得新旧知识能够紧密结合，彼此交融；不论是通过同化的方式还是顺应的方式，这种联系都能促进新知识顺利融入或扩展至学生的数学认知结构中。比如，在教学“异分母分数加减法”“小数加减法”及“整数加减法”时，应引导学生发现其中核心共性——对相同计数单位数量的运算，当学生能够领会这一共同点，他们便能更深入地理解并有效运用这些运算法则。

（三）突出数学本质，提高概括水平

在小学生数学学习的进程中，迁移能力的强弱与其数学概括能力的高低密切相关。因此，教师在教学时应注重数学本质的教学，致力于提升学生的数学概括能力，以此来推动学生主动进行知识的迁移与运用。比如，在教学“面积的认识”时，教师可以将生活常见物品的表面（如桌面、数学书封面和黑板面等）与教学内容进行关联，并鼓励他们进行比较分析。在此基础上，教师可以进一步将教学延伸至课后，让学生根据课上所学内容在生活中测量物体的面积。

（四）培养类比能力，提高迁移效果

类比推理是一种基于两个对象间共同或相似性质的推理方式，它假设这些对象在其他未直接观察到的性质上也可能具有相同或相似的特点。这些共同或相似的属性，称之为共同要素。在小学数学教学中，类比方法被广泛应用。当学生面对新知识时，他们会通过与已学过的旧知识进行观察比较，找出它们之间的相似特征，从而揭示它们的本质属性及其关系。通过这样的思维过程，学生会自然而然地将旧问题的解决方法应用到新问题中，实现知识的迁移。

三、促进学习迁移现实应用的价值关联

（一）学习迁移：引导多元反思

在数学课程设计中，教师应聚焦于学习迁移的核心目的，培养学生在各种情境中灵活运用所学知识与基本技能解决数学实际问题的能力。课程的整体架构致力于引导学生深入理解数学原理、策略及其价值，进而推动他们经验的累积与数学素养的整体提升。以“多边形的面积”单元教学为例，该单元涉及求组合图形面积内容，这是基本图形面积的延伸，更是往后学生学习立体图形的基础，具有显著的迁移性和可拓展性。

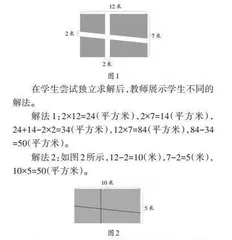
【示例1】校园里有一块草坪（如图1），中间有人行道穿过。这个草坪的面积是多少平方米？

为了使学生能够深刻领会并辨析这两种解法，教师要求学生详细阐述每种解法的思路。第一种解法是先计算人行道的面积，然后从总面积中减去人行道的面积，从而得出草坪的实际面积。这种思路虽然比较直观，但在面对复杂情况时可能会导致计算量的增加。第二种解法则运用了平移思想，巧妙地将四块草坪拼成一个长方形。这种解法不仅简化了计算过程，还渗透了平移思想。通过对比这两种解法思路，可以拓宽学生的思维路径，从而在选择解题方法时更加灵活和高效。

引导比较：你喜欢哪种解法？你能给第二种解法起个名字吗？（平移化整）

教师小结：在解决实际问题时，多边形面积的计算方法并不仅限于分割法和添补法，还可以巧妙地运用“平移化整”策略，通过平移将分割后的多个图形部分重新组合成一个更为规则的基本图形，从而简化计算过程。

在对“分割求和”与“添补求差”这两种基本数学方法进行深入研究后，学生逐渐形成了一种“分解与整合”的数学思维模式。他们了解到，多边形可以解构为简单的基本图形进行分析，而这些基本图形亦能组合成更复杂的多边形。这种数学思维模式在本教学环节中得到了充分的培养和应用，有助于学生形成整体与部分结合分析的解题思路。教师特意引导学生将这种分解与组合的思想运用到实际问题中，让他们在实践中感悟整体思维的魅力，并通过举一反三的方式，将这一思维模式内化于解题过程之中。

（二）学习迁移：感悟数学思想

学习迁移的核心宗旨是提升学生的高阶思维能力，使他们对某一知识点能够进行更高层次的迁移应用。在追求深度学习的数学复习课程中，教师应着重通过“知识创新”的方式，点燃学生的思维火花。不仅要引导他们摆脱传统的解题思路，更要培养他们面对稍微复杂问题时，能够提出并实践超越教材标准的新知识或新方法。

【示例2】某小学有一直角梯形花圃（如图3）。这个花圃的区域①和②为两个等腰直角三角形，分别种植了月季和玫瑰，而剩下的区域③则种植了牡丹。请根据图3的数据计算出这个花圃的总面积。

思路分析：为了求得这个花圃的总面积，首要步骤是将该问题细分为计算①②③三个区域的面积。鉴于①和②是等腰直角三角形，我们可以合理推测③也是一个直角三角形。

解法探究：在学生经历了几何图形的组合探究后，教师可以组织学生进行讨论，并引导他们思考，是否可以通过某种方式（如添补法）来转化这些三角形，形成规则易求的几何图形。通过讨论和尝试，学生会发现，可以通过添补法将三角形①转化为一个直角边为18米的等腰直角三角形的一半，从而轻松地求出其面积；同理，其他学生也能受到启发，运用类似的逻辑将三角形②变形为一个直角边为24米的等腰直角三角形的一半（如图4）。

教师小结：通过这道题可以发现，添补法的精简与高效，它在解决某些看似棘手问题时能起到强大作用。解决这道题的过程中，引导学生先是认识再到迁移应用这种方法。

综上所述，在小学数学的教学实践中，教师应聚焦于引导学生深入理解数学知识的核心原理，让学生把握数学知识间的内在关联，进而实现旧知识向新知识的有效迁移。通过精心策划和实施学习迁移策略，教师可以有效地激发学生的思考潜能，丰富其解题思路，进而提高其学习效率和思维能力。此外，教师还须根据学生的个性化需求和学习特点，灵活调整学习迁移策略，以促进每名学生的全面发展。

［ 参 考 文 献 ］

[1] 程明喜，王宽明.从“数学实质”到“数学本质”：2011年版与2022年版《义务教育数学课程标准》比较研究[J].教育学术月刊，2023（8）：80-86.

[2] 吴永云.浅谈小学数学教学中的启发诱导[J].黔东南民族师专学报，2000（6）：93-94.

[3] 黄振锋.基于学习迁移下的小学数学思维训练策略[J].亚太教育，2019（6）：54.

[4] 何玮琪.小学高段数学学困生的成因及转化策略研究[J].齐齐哈尔师范高等专科学校学报，2021（3）：118-120.

[5] 姜银成，王银.浅谈小学生数学学习迁移能力培养策略[J].甘肃教育研究，2023（3）：45-47.

（责编    梁桂广）