初中数学教学中“三环五步”教学模式的研究

【摘要】初中数学是整个数学学习的关键时期，在整个数学知识体系中占有重要地位。为了达到数学的课程目标，本文以《义务教育数学课程标准》为指导，根据本校教学实践情况，探索如何将“三环五步”教学模式应用于初中数学之中。在数学学习的过程中，学生能够学会对数学知识进行探究，并表达出自己的想法和思路。

【关键词】三环五步  教学模式  设计过程

【中图分类号】G633.6   【文献标识码】A 【文章编号】2095-3089（2024）08-0175-03

初中阶段，学生的思维活跃，参与课堂学习的积极性较高，教师可以根据此学情激发学生探索知识的兴趣。按照下文所示模式，师生课前认真准备，课上在教师的引导下，学生进行小组合作展示、应用练习、总结知识等步骤，进而使学生达到掌握新知的目的。

一、“三环五步”教学模式的理论基础

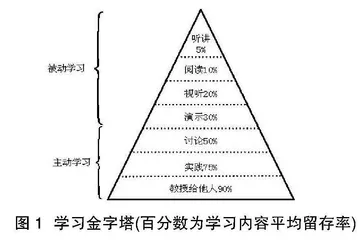
哈尔莫斯说：“数学之美是很自然明白地摆着的。”建构主义学习理论强调，在教学过程中，学生应该是学习的主体，教师应该积极引导学生学习，从建构主义理论出发，在已有知识的基础之上，发散思维，积极创新，不断提高能力，让学生真正成为主动建构者和课堂的主人。其实也就是教育学中体现的新知识要站在已有的知识之上。夸美纽斯说过：“一切知识都是从感官开始的。”我们在实际的教学过程中，可以采用情境教学的方法。下图1为学习金字塔。

图1  学习金字塔（百分数为学习内容平均留存率）

二、初中数学教学中“三环五步”教学模式的步骤

这个模式是在学校教育教学过程中，不断总结以往经验，按照教学大纲、教材内容、学情分析、课后指导等构建课程，以此来提高学生的学习效率和在数学学习中的合作、探究能力。根据图2，我们可以看出“三环五步”不仅指出了课堂教学中引导启发学生和课堂练习的重要作用，而且把课前预习和课后复习纳入此模式中。每次上课之前，学生要按照教师布置的任务进行预习，得知本节课的基本知识，在课上，教师通过精心设计的导入环节，让学生对本节课的学习产生好奇心，提出本节课的重难点，引出需要解决的问题，通过同学互助、小组交流、课上练习等途径，重点让学生经历学、讲、练的过程，发挥主观作用，提高课堂效率，达到掌握本节课知识的目的。

图2  初中数学“三环五步”的步骤

在教学实际中，我们可以将数学课本章节分成以下类型。

理论型：在二次根式的教学中，二次根式的概念、性质、运算法则（加、减、乘、除）。这些内容和以前学习的字母表示数和实数等知识有很大的联系，在进行课中五步过程中，精彩导入、新知讲解、应用练习、小组讨论总结、当堂检测。上课时，老师要讲解细致，多给学生留出练习的时间，做到当堂任务当堂必须解决。

以二次根式性质的教学过程为例：

（一）旧知回顾

（二）探究新知

（三）知识归纳

（四）典例赏析及练习

例1  已知实数a，b在数轴上的位置如图所示，化简：■＋■－|a-b|

例2  下列式子不是代数式的是（  ）

A.4a       B.■         C.y＞1        D.b－3

练习：

1.教材第3页，练习。

2.若■=7-m，则m的取值范围是______。

（五）课堂小结

探究型：初中数学中有许多关于几何知识的教学内容，这部分内容比较直观，但是某些定理还是需要学生们去发现特点。课堂环节有导入情景、探究新知、归纳总结、当堂检测等，学生学会观察图形，描述图形的共同特征，总结图形的特殊性。

以勾股定理为例：

（一）情景引入

（二）新知探究

探究一：你能发现图中正方形A、B、C的面积之间有什么数量关系吗？

探究二：证明定理。

（三）拓展应用

在Rt△ABC中，∠C=90°，∠A，∠B，∠C的对边分别为a，b，c

（1）已知a=3，b=4，则c=____

（2）已知c=15，b=12，则a=____

（3）已知a=5，c=13，则b=____

（四）归纳总结

本节课应掌握： 1．a2+b2=c2

2．在生活实践中学会使用勾股定理。

（五）当堂检测

实践型：数学知识有些是和生活知识相联系的，并可以用来处理现实难题，是数学与社会、数学与实际的重要内容，可以帮助学生提高学数学的效率。实践型五步为精彩导入、小组讨论、归纳总结、实践应用、当堂检测。在课上，老师要将更多的时间留给学生，让他们根据学习目标，以小组合作的方式共同寻找解决难题的办法，拓宽数学知识面，解决现实中的问题，提高数学能力。

某学校八年级有4个班，共有180人，其中男生85人，女生95人。表1是用来记录学生体质健康测试结果的登记表。

表1  学生体质健康测试结果登记表

（一）收集数据

1.确定样本

2.确定抽取样本的方法

（二）整理数据

例如计算每个个体的最后得分，按评分标准整理样本数据，得到表2：

表2

（三）描述数据

根据表2可以画出条形图和扇形图。

（四）分析数据

按照已获得的相关数据资料，我们可以利用相关统计知识得到数据的平均数、中位数、极差、方差等，并获取结果。

根据表2和相关条形图和扇形图可知，样本的体质健康成绩达到良好的最多，有17人，良好及以上的有29人，约占统计人数的70％左右，由此可以估计全校八年级学生的体质健康成绩有类似的结果。

（五）撰写调查报告

最后，根据前期收集的数据，与学生的沟通交流，撰写调查报告，进而得出结论并向大家公布，鼓励学生继续努力不断进步。

三、初中数学教学中“三环五步”教学模式的设计过程

数学教学中，数学的理论知识尤为重要，这里选择七年级数学“正数和负数”来说明“三环五步”教学模式的运用。

第一环课前，让同学们自己去找温度计，观察温度计上的数字表达什么含义。做实验测量开水、自来水和冰块的温度，并记录所测量的数据。让学生自己体验一下自来水温度和冰块的温度，并写出感受。

第二环课中五步

第一步精彩导入：某市某一天的最高温度是零上5℃，最低温度是零下5℃，如何来表示这两个温度？如何把这两个量表达得更加简洁清楚，以前学过的数还可以用吗？可不可以通过引入新的数来表示这些量呢？本节课我们学习新的内容——正数与负数，看看这些数能不能表示前面的两个量。

第二步新知探究：

在平常生活中，常常会这样表达一些数量：

（1）小明向北走13步和向南走了22步。

（2）家庭每天收入400元和支出137元。

（3）河水水位升高1.2 m和下降0.7 m。

（4）买进50辆汽车和卖出30辆汽车。

小组讨论：上面例子中出现的量有什么特点？是不是成对量出现的？每个问题的内容不同，但是都有一个共同点，这个共同点是什么？

第三步拓展应用：

例1 一年的时间，小李体重增加4斤，小王体重减少2斤，小豆体重无变化。将小李、小王和小豆的体重减少值表示出来。

例2 与2021年相比，2022年6国GDP增长如下：美国增长1.4％，尼日利亚增长2.3％，瑙鲁减少2.5％，英国减少0.5％，意大利增长0.5％，阿尔巴尼亚增长3.5％，请写出这一年，上述几国GDP增长率。

分析：首先我们来弄清楚增长-0.5是什么意思？增长-2.5％是什么意思？

增长-0.5表示减少0.5；因此增长-2.5％表示减少2.5％。

解：（1）一年的时间，小李体重增长4斤，小王体重增长-2公斤，小豆体重增长0斤。

（2）2022年，上述几国GDP增长率分别为：

美国增长1.4％，尼日利亚增长2.3％

瑙鲁增长-2.5％，英国增长-0.5％

意大利增长0.5％，阿尔巴尼亚增长3.5％

强调：在表述同样的一个问题时，正数和负数表示具有相反意义的量。

例3  “佳佳”牌的瓶装饮料外包装上有“550±20（mL）”字样，请大家讨论一下“550±20（mL）”是什么含义？国家质监局对该饮料进行了抽查检验，抽取其中5瓶，它们的容量分别为553 mL，561 mL，539 mL，533 mL，562 mL，请问所查饮料的容量是否合格？分析：“+20”是什么意思？“-20”是什么意思？

解：饮料容积“550±20（mL）”表示实际容量比550mL最多多20mL，最少少20mL，即在530～570之间。因此，所查饮料的容量在530～570mL之间，所以都是在合格的范围内。

第四步归纳总结：

共同特点：以上问题具有相反的意义，如向南和向北、收入和支出、升高和下降、零上和零下等具有相反的意义。

问题：同学们，你们能不能开动一下自己的小脑袋，想一想生活中你所听所见过的表示相反意义的例子呢？

归纳：看来同学们非常用心观察生活，能够发现那么多相反意义的量。老师认为相反意义的量应该包含两个方面：（1）应该具有相反的意义。（2）有一定的量值。

收入400元和支出137元，是一对有相反意义的量。升高和下降只具有相反的意义，没有数量关系，因此不是相反意义的量。

第五步当堂检测

练一练：课本第4页，练习

同步学习第2页，课堂过关

第三环课后任务：设计一定数量和难度的作业，要求学生先独立思考，组长检查后，教师抽查部分学生完全的作业情况，并根据学生完成实际，有针对性地进行讲解分析。课后，安排同桌间相互提问、讲解。最后使全体同学都能够有所收获。

四、总结

“三环五步”教学模式是按照新的课程理念，将该模式应用到初中数学教学中，能够优化学生学习数学的方式，增强学生探究数学的兴趣。“三环五步”教学模式在课前和课后中能够使得学生对课堂知识点进行“备课”，课中五步体现数学学习的发现过程，使得学生学习到获取知识和技能的方式和方法。“三环五步”教学模式重建了教和学的关系，在交流和探讨中获得知识，发挥主观能动性，符合学习金字塔理论。